Prim算法和Kruskal算法介绍

一、Prim算法

普利姆(Prim)算法适用于求解无向图中的最小生成树(Minimum Cost Spanning Tree)。下面是Prim算法构造最小生成树的过程图解。

                              

                                                          

                                                           

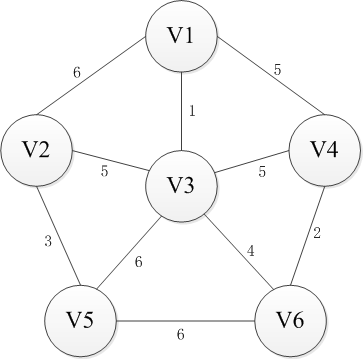
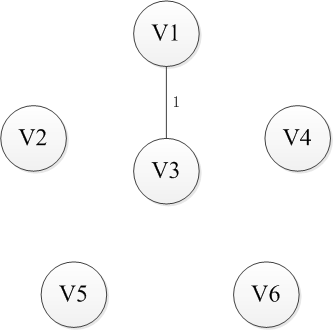
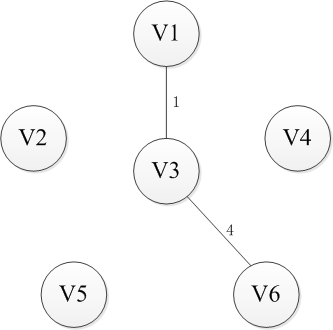
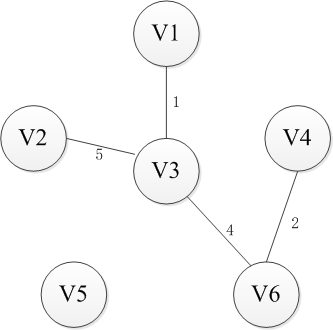
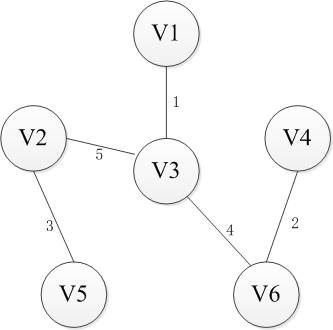
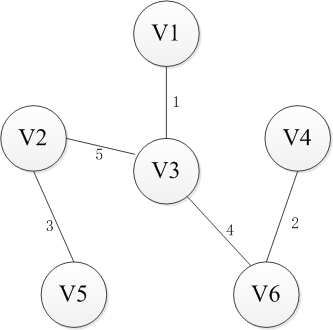
选择一个节点开始，比如V1进入集合U，剩下的集合的V-U包括剩下的节点，然后寻找从集合U到集合V-U最近的路径。这里有三条路径分别是权重为6到V2，权重为5到V4以及权重为1到V3，显然到通过V3连接而集合U和集合V-U是最近的，选择V3进入集合U。同样继续选择到V-U的路径，此时有6条可选路径，分别是权为6到V2【从V1】，权为5到V4【从V1】，权为5到V2【从V3】，权为5到V4【从V3】，权为6到V5【从V3】，权为4到V6【从V3】。选择出从V3到V6的路径并将V6添加至集合U中。按照这种方法依次将V4，V2和V5添加到集合U直到U和全体节点结合V相等，或者说V-U集合为空时结束，这时选出的n-1条边即为最小生成树。

二、Kruskal算法

克鲁斯卡尔(Kruskal)算法是另一种求解最小生成树的算法。下面是Kruskal算法构造最小生成树的过程图解。

                                                   

                                                                                                                                                            

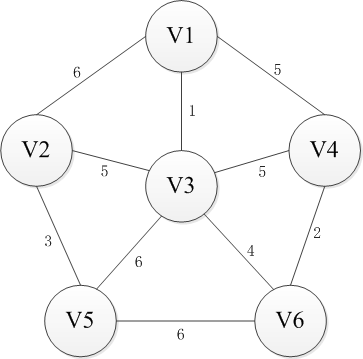
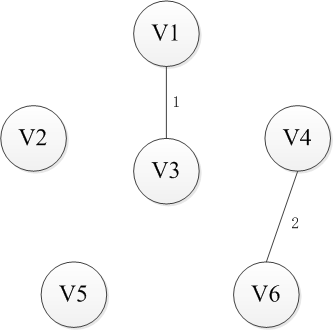
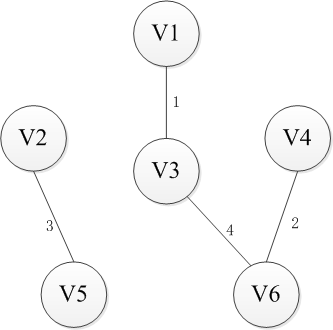
Kruskal则是采取另一种思路，即从边入手。首先n个顶点分别视为n个连通分量，然后选择一条权重最小的边，如果边的两端分属于两个连通分量，就把这个边加入集合E，否则舍去这条边而选择下一条代价最小的边，依次类推，直到所有节点都在同一个连通分量上。

三、对比

假设网中有n个节点和e条边，普利姆算法的时间复杂度是O(n^2)，克鲁斯卡尔算法的时间复杂度是O(eloge)，可以看出前者与网中的边数无关，而后者相反。因此，普利姆算法适用于边稠密的网络而克鲁斯卡尔算法适用于求解边稀疏的网。