一文搞定AB测试
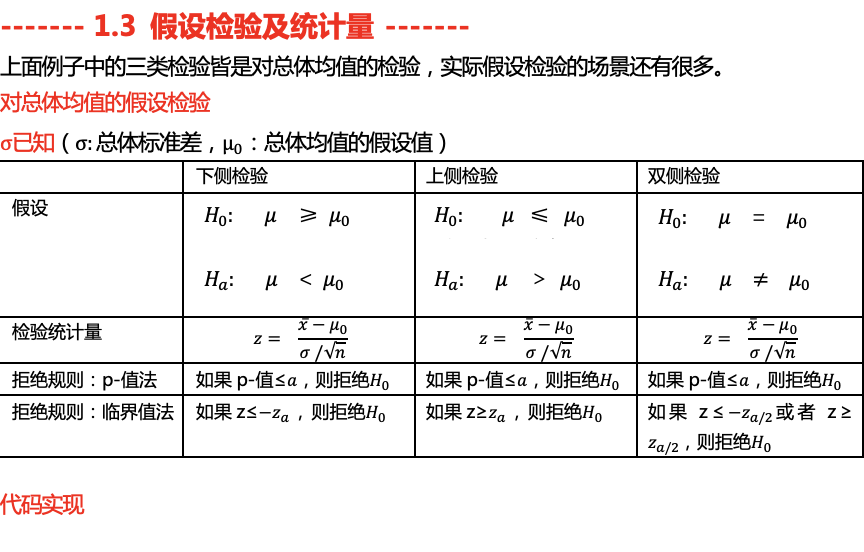
import numpy as np
import scipy.stats as stats
import pandas as pd
'''
场景：当已知总体标准差，对总体均值进行估计，用z检验
'''
def single_sample_mean_test_z(sample_size,sample_mean,alpha,entirety_mean,entirety_std,tail_type): # 参数分别为样本量，样本均值，显著性，总体均值的假设值，总体标准差,上下侧检验分类
"""
接口请求参数:{
"sample_size": "", # int,参数分别为样本量
"sample_mean": "", # float,样本均值
"alpha":"", # float,显著性
"entirety_mean": "", # float,总体均值的假设值
"entirety_std":"", # float,总体标准差
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
z = (sample_mean - entirety_mean) / (entirety_std / np.sqrt(sample_size)) # 总体标准差已知时，代入求z值
p = stats.norm.sf(abs(z))*2 # 由z值计算p值,注意这里的绝对值
lower = -stats.norm.ppf( alpha / 2) # 根据显著性求临界值
upper = stats.norm.ppf(alpha / 2) # 根据显著性求临界值
critical_lower = min(lower,upper)
critical_upper = max(lower,upper)
# 双侧检验
if tail_type == 'two':
if ((abs(z) >= abs(critical_lower)) or (abs(z) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title":"已知总体标准差，对总体均值进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a":alpha,
"conclusion":"双侧检验，拒绝原假设!!!"
},index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对总体均值进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
},index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (z <= critical_lower) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对总体均值进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对总体均值进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (z >= critical_upper) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对总体均值进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对总体均值进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
if __name__ == '__main__':
# 样本量：50
# 样本均值：297.6
# 显著性水平：0.05
# 总体均值的假设值：295
# 总体标准差：12
conclusion = single_sample_mean_test_z(50,297.6,0.05,295,12,'two')
print(conclusion)
# 样本量：36
# 样本均值：2.92
# 显著性水平：0.01
# 总体均值的假设值：3
# 总体标准差：0.18
conclusion_downside = single_sample_mean_test_z(36,2.92,0.01,3,0.18,'downside')
print(conclusion_downside)
# 样本量：40
# 样本均值：26.4
# 显著性水平：0.01
# 总体均值的假设值：25
# 总体标准差：6
conclusion_upside = single_sample_mean_test_z(40,26.4,0.01,25,6,'upside')
print(conclusion_upside)
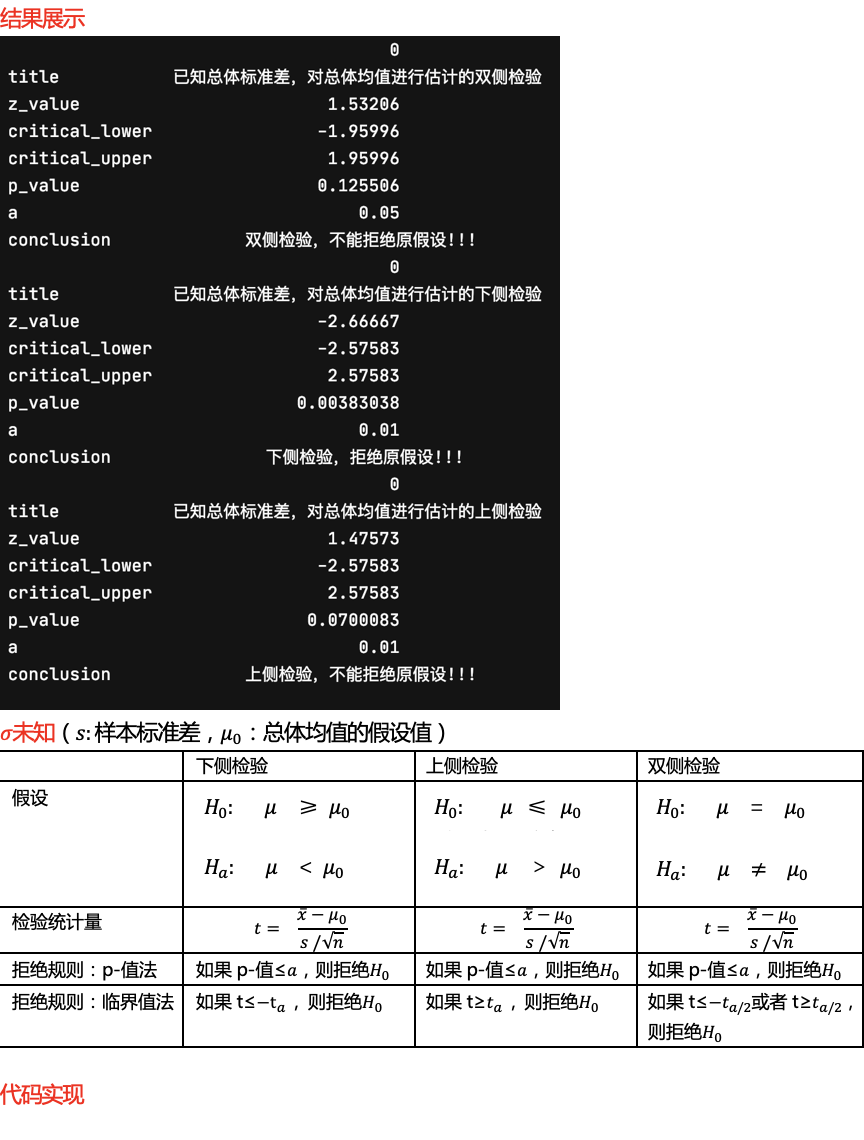
from scipy.stats import ttest_1samp
import numpy as np
import pandas as pd
from scipy.stats import t
'''
场景：当总体标准差未知，对总体均值进行估计，用t检验，用样本标准差代替总体标准差
'''
def single_sample_mean_test_t(sample_size,sample_mean,alpha,entirety_mean,sample_std,tail_type): # 参数分别为样本量，样本均值，显著性，总体均值的假设值，总体标准差,上下侧检验分类
"""
接口请求参数:{
"data":"", #
"sample_size": "", # int,参数分别为样本量
"sample_mean": "", # float,样本均值
"alpha":"", # float,显著性
"entirety_mean": "", # float,总体均值的假设值
"sample_std":"", # float,样本标准差
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
df = sample_size - 1 # 自由度
tt = (sample_mean - entirety_mean) / (sample_std / np.sqrt(sample_size)) # 总体标准差未知时，用样本标准差代替，代入求t值
p = t.sf(tt, df)*2 # 由t值计算p值
# tt, p = ttest_1samp(data, entirety_mean) # t值和p值
# ttest_ind ttest_rel
lower = -t.ppf( alpha / 2,df) # 根据显著性求临界值
upper = t.ppf(alpha / 2,df) # 根据显著性求临界值
critical_lower = min(lower,upper)
critical_upper = max(lower,upper)
# 双侧检验
if tail_type == 'two':
if ((abs(tt) >= abs(critical_lower)) or (abs(tt) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title":"未知总体标准差，对总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a":alpha,
"conclusion":"双侧检验，拒绝原假设!!!"
},index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
},index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (tt <= critical_lower) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (tt >= critical_upper) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
def single_sample_mean_test_t_normal(data,alpha,entirety_mean,tail_type): # 参数分别为样本量，样本均值，显著性，总体均值的假设值，总体标准差,上下侧检验分类
"""
接口请求参数:{
"data":"", #
"sample_size": "", # int,参数分别为样本量
"sample_mean": "", # float,样本均值
"alpha":"", # float,显著性
"entirety_mean": "", # float,总体均值的假设值
"sample_std":"", # float,样本标准差
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
df = len(data) - 1 # 自由度
# tt = (sample_mean - entirety_mean) / (sample_std / np.sqrt(sample_size)) # 总体标准差未知时，用样本标准差代替，代入求t值
# p = t.sf(tt, df)*2 # 由t值计算p值
tt, p = ttest_1samp(data, entirety_mean) # t值和p值
lower = -t.ppf( alpha / 2,df) # 根据显著性求临界值
upper = t.ppf(alpha / 2,df) # 根据显著性求临界值
critical_lower = min(lower,upper)
critical_upper = max(lower,upper)
# 双侧检验
if tail_type == 'two':
if ((abs(tt) >= abs(critical_lower)) or (abs(tt) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title":"未知总体标准差，对总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a":alpha,
"conclusion":"双侧检验，拒绝原假设!!!"
},index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
},index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (tt <= critical_lower) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (tt >= critical_upper) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "未知总体标准差，对总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
if __name__ == '__main__':
# 样本量：25
# 样本均值：37.4
# 显著性水平：0.05
# 总体均值的假设值：40
# 样本标准差：11.79
conclusion = single_sample_mean_test_t(25,37.4,0.05,40,11.79,'two')
print(conclusion)
# 样本量：36
# 样本均值：44
# 显著性水平：0.05
# 总体均值的假设值：45
# 样本标准差：5.2
conclusion_downside = single_sample_mean_test_t(36,44,0.05,45,5.2,'downside')
print(conclusion_downside)
# 样本量：60
# 样本均值：7.25
# 显著性水平：0.05
# 总体均值的假设值：7
# 样本标准差：1.052
conclusion_upside = single_sample_mean_test_t(60,7.25,0.05,7,1.052,'upside')
print(conclusion_upside)
list = [1,2,3,4,5,6,7,8,9,10]
data = pd.DataFrame({"X": list})
# 显著性水平：0.05
# 总体均值的假设值：7
conclusion_n = single_sample_mean_test_t_normal(data,0.05,3,'upside')
print(conclusion_n)
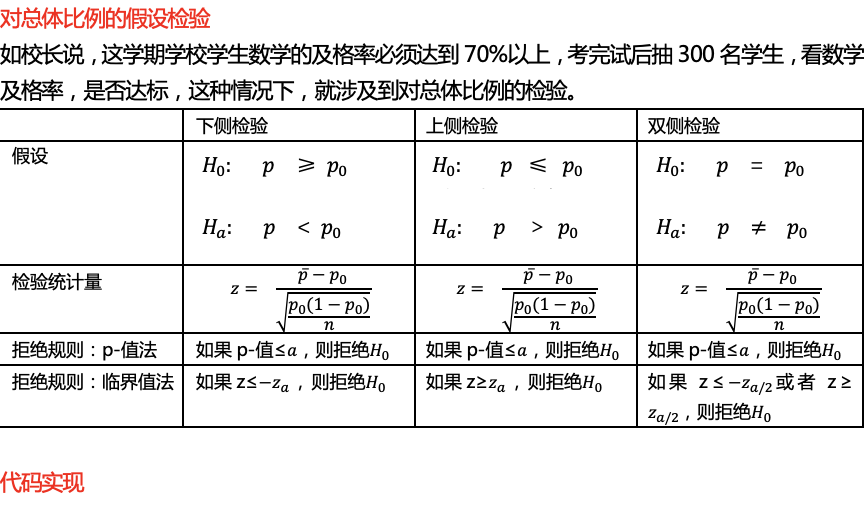
import numpy as np
import scipy.stats as stats
import pandas as pd
'''
场景：对总体比率进行估计，用z检验
'''
def single_sample_ratio_test_z(sample_size,sample_ratio,alpha,entirety_ratio,tail_type): # 参数分别为样本量，样本均值，显著性，总体均值的假设值，总体标准差,上下侧检验分类
"""
接口请求参数:{
"sample_size": "", # int,参数分别为样本量
"sample_ratio": "", # float,样本比率
"a":"", # float,显著性
"entirety_ratio": "", # float,总体比率的假设值
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
z = (sample_ratio - entirety_ratio) / np.sqrt(entirety_ratio*(1-entirety_ratio)/sample_size) # 总体标准差已知时，代入求z值
p = stats.norm.sf(abs(z))*2 # 由z值计算p值,注意这里的绝对值
lower = -stats.norm.ppf( alpha / 2) # 根据显著性求临界值
upper = stats.norm.ppf(alpha / 2) # 根据显著性求临界值
critical_lower = min(lower,upper)
critical_upper = max(lower,upper)
# 双侧检验
if tail_type == 'two':
if ((abs(z) >= abs(critical_lower)) or (abs(z) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title":"对总体比率进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a":alpha,
"conclusion":"双侧检验，拒绝原假设!!!"
},index=[0]).T
else:
return pd.DataFrame({
"title": "对总体比率进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
},index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (z <= critical_lower) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "对总体比率进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "对总体比率进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (z >= critical_upper) or (p/2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "对总体比率进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "对总体比率进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p/2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
if __name__ == '__main__':
# 样本量：400
# 样本比率：0.25
# 显著性水平：0.05
# 总体比率的假设值：0.2
conclusion = single_sample_ratio_test_z(400,0.25,0.05,0.2,'two')
print(conclusion)
# 样本量：400
# 样本比率：0.25
# 显著性水平：0.05
# 总体比率的假设值：0.2
conclusion_downside = single_sample_ratio_test_z(400,0.25,0.05,0.2,'downside')
print(conclusion_downside)
# 样本量：400
# 样本比率：0.25
# 显著性水平：0.05
# 总体比率的假设值：0.2
conclusion_upside = single_sample_ratio_test_z(400,0.25,0.05,0.2,'upside')
print(conclusion_upside)
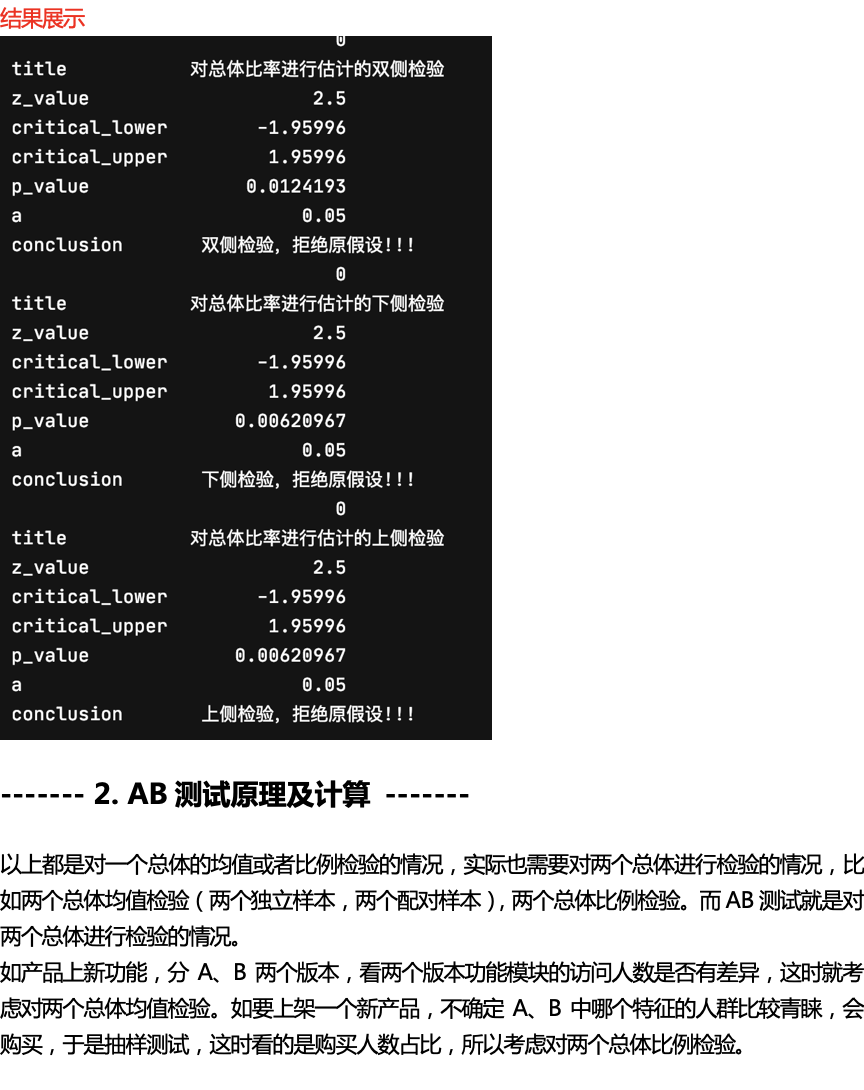
import numpy as np
import scipy.stats as stats
import pandas as pd
'''
场景：对两个独立总体均值进行估计,已知两个总体的标准差，用z检验
'''
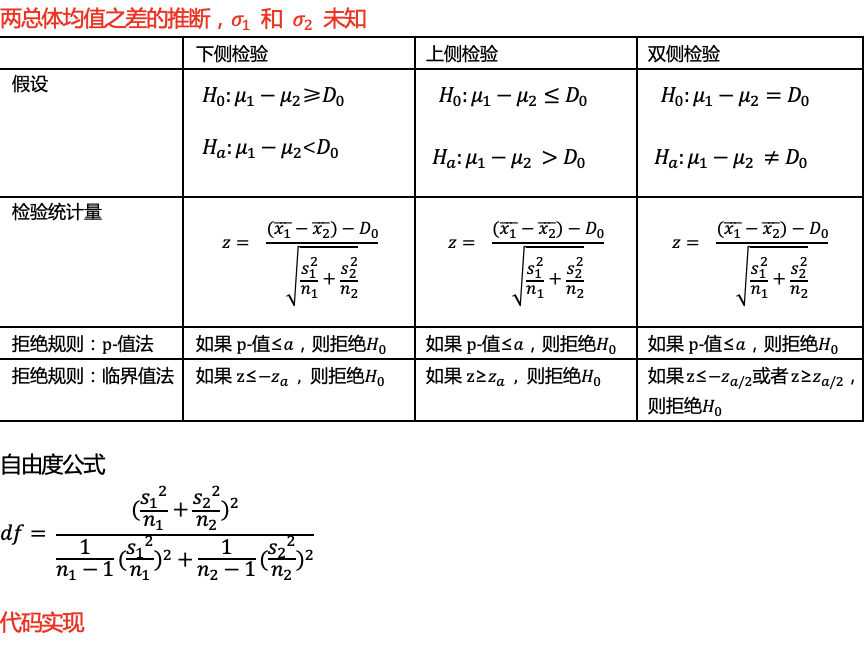
def two_sample_independent_mean_test_z(sample_size1, sample_size2, sample_mean1, sample_mean2, alpha, entirety_diff,
entirety_std1, entirety_std2,
tail_type):
"""
接口请求参数:{
"sample_size1": "", # int,第一个样本的样本量
"sample_size2": "", # int,第二个样本的样本量
"sample_mean1": "", # float,第一个样本的均值
"sample_mean2": "", # float,第二个样本的均值
"a":"", # float,显著性
"entirety_diff":"", # float,两个总体均值差的假设值
"entirety_std1": "", # float,第一个总体标准差
"entirety_std2":"", # float,第二个总体标准差
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
z = ((sample_mean1 - sample_mean2) - entirety_diff) / np.sqrt((entirety_std1 * entirety_std1 / sample_size1) + (
entirety_std2 * entirety_std2 / sample_size2)) # 总体标准差已知时，代入求z值
p = stats.norm.sf(abs(z)) * 2 # 由z值计算p值,注意这里的绝对值
lower = -stats.norm.ppf(alpha / 2) # 根据显著性求临界值
upper = stats.norm.ppf(alpha / 2) # 根据显著性求临界值
critical_lower = min(lower, upper)
critical_upper = max(lower, upper)
# 双侧检验
if tail_type == 'two':
if ((abs(z) >= abs(critical_lower)) or (abs(z) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (z <= critical_lower) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (z >= critical_upper) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
if __name__ == '__main__':
# 样本量1：30
# 样本量2：40
# 样本均值1：82
# 样本均值2：78
# 显著性水平：0.05
# 总体均值差的假设值：0
# 总体标准差1：10
# 总体标准差2：10
conclusion = two_sample_independent_mean_test_z(30, 40, 82, 78, 0.05, 0, 10, 10, 'two')
print(conclusion)
# 样本量1：30
# 样本量2：40
# 样本均值1：82
# 样本均值2：78
# 显著性水平：0.05
# 总体均值差的假设值：0
# 总体标准差1：10
# 总体标准差2：10
conclusion_downside = two_sample_independent_mean_test_z(30, 40, 82, 78, 0.05, 0, 10, 10, 'downside')
print(conclusion_downside)
# 样本量1：30
# 样本量2：40
# 样本均值1：82
# 样本均值2：78
# 显著性水平：0.05
# 总体均值差的假设值：0
# 总体标准差1：10
# 总体标准差2：10
conclusion_upside = two_sample_independent_mean_test_z(30, 40, 82, 78, 0.05, 0, 10, 10, 'upside')
print(conclusion_upside)
from statsmodels.stats.diagnostic import lilliefors
import numpy as np
import scipy.stats as stats
import pandas as pd
import scipy, math
from scipy.stats import t
'''
场景：对两个独立总体均值进行估计，两个总体标准差未知，用样本标准差代替，用t检验
'''
def two_sample_independent_mean_test_t(sample_size1, sample_size2, sample_mean1, sample_mean2, alpha, entirety_diff,
sample_std1, sample_std2,
tail_type):
"""
接口请求参数:{
"sample_size1": "", # int,第一个样本的样本量
"sample_size2": "", # int,第二个样本的样本量
"sample_mean1": "", # float,第一个样本的均值
"sample_mean2": "", # float,第二个样本的均值
"a":"", # float,显著性
"entirety_diff":"", # float,两个总体均值差的假设值
"sample_std1": "", # float,第一个样本标准差
"sample_std2":"", # float,第二个样本标准差
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
tt = ((sample_mean1 - sample_mean2) - entirety_diff) / np.sqrt((sample_std1 * sample_std1 / sample_size1) + (
sample_std2 * sample_std2 / sample_size2)) # 总体标准差已知时，代入求z值
df = (((sample_std1 * sample_std1 / sample_size1) + (sample_std2 * sample_std2 / sample_size2))*((sample_std1 * sample_std1 / sample_size1) + (sample_std2 * sample_std2 / sample_size2)))/\
((1/(sample_size1-1)*(sample_std1 * sample_std1 / sample_size1)*(sample_std1 * sample_std1 / sample_size1))+((1/(sample_size2-1)*(sample_std2 * sample_std2 / sample_size2)*(sample_std2 * sample_std2 / sample_size2))))
p = t.sf(tt, df) * 2 # 由t值计算p值
lower = -t.ppf( alpha / 2,df) # 根据显著性求临界值
upper = t.ppf(alpha / 2,df) # 根据显著性求临界值
critical_lower = min(lower,upper)
critical_upper = max(lower,upper)
# 双侧检验
if tail_type == 'two':
if ((abs(tt) >= abs(critical_lower)) or (abs(tt) >= abs(critical_upper))) or (p <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的双侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (tt <= critical_lower) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的下侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (tt >= critical_upper) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体均值进行估计的上侧检验",
"t_value": tt,
"degrees_of_freedom": df,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
'''
正态性检验
'''
# alpha = 0.05
def check_normality(testData, alpha=0.05):
# 20<样本数<50用normal test算法检验正态分布性
if 20 < len(testData) < 50:
normaltest_statistic, normaltest_p = stats.normaltest(
testData) # https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.stats.normaltest.html
print(normaltest_statistic, normaltest_p)
if normaltest_p < alpha:
print('use normaltest')
# print('data are not normal distributed')
print('数据不符合正态分布！')
return False
else:
print('use normaltest')
# print('data are normal distributed')
print('数据符合正态分布！')
return True
# 样本数小于50用Shapiro-Wilk算法检验正态分布性
if len(testData) < 50:
shapiro_statistic, shapiro_p = stats.shapiro(
testData) # Perform the Shapiro-Wilk test for normality. https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.stats.shapiro.html
print(shapiro_statistic, shapiro_p)
if shapiro_p < alpha:
print("use shapiro:")
# print("data are not normal distributed")
print('数据不符合正态分布！')
return False
else:
print("use shapiro:")
# print("data are normal distributed")
print('数据符合正态分布！')
return True
if 300 >= len(testData) >= 50:
lilliefors_statistic, lilliefors_p = lilliefors(
testData) # https://blog.csdn.net/qq_20207459/article/details/103000285
print(lilliefors_statistic, lilliefors_p)
if lilliefors_p < alpha:
print("use lillifors:")
# print("data are not normal distributed")
print('数据不符合正态分布！')
return False
else:
print("use lillifors:")
# print("data are normal distributed")
print('数据符合正态分布！')
return True
if len(testData) > 300:
kstest_statistic, kstest_p = scipy.stats.kstest(testData, 'norm')
print(kstest_statistic, kstest_p)
if kstest_p < alpha:
print("use kstest:")
# print("data are not normal distributed")
print('数据不符合正态分布！')
return False
else:
print("use kstest:")
# print("data are normal distributed")
print('数据符合正态分布！')
return True
# 对所有样本组进行正态性检验
# 先将各个样本分好，对所有样本检验正态性，也是对样本组里的每个样本检验
def NormalTest(list_groups, alpha):
for group in list_groups:
# 正态性检验
status = check_normality(group, alpha)
if status == False:
return False
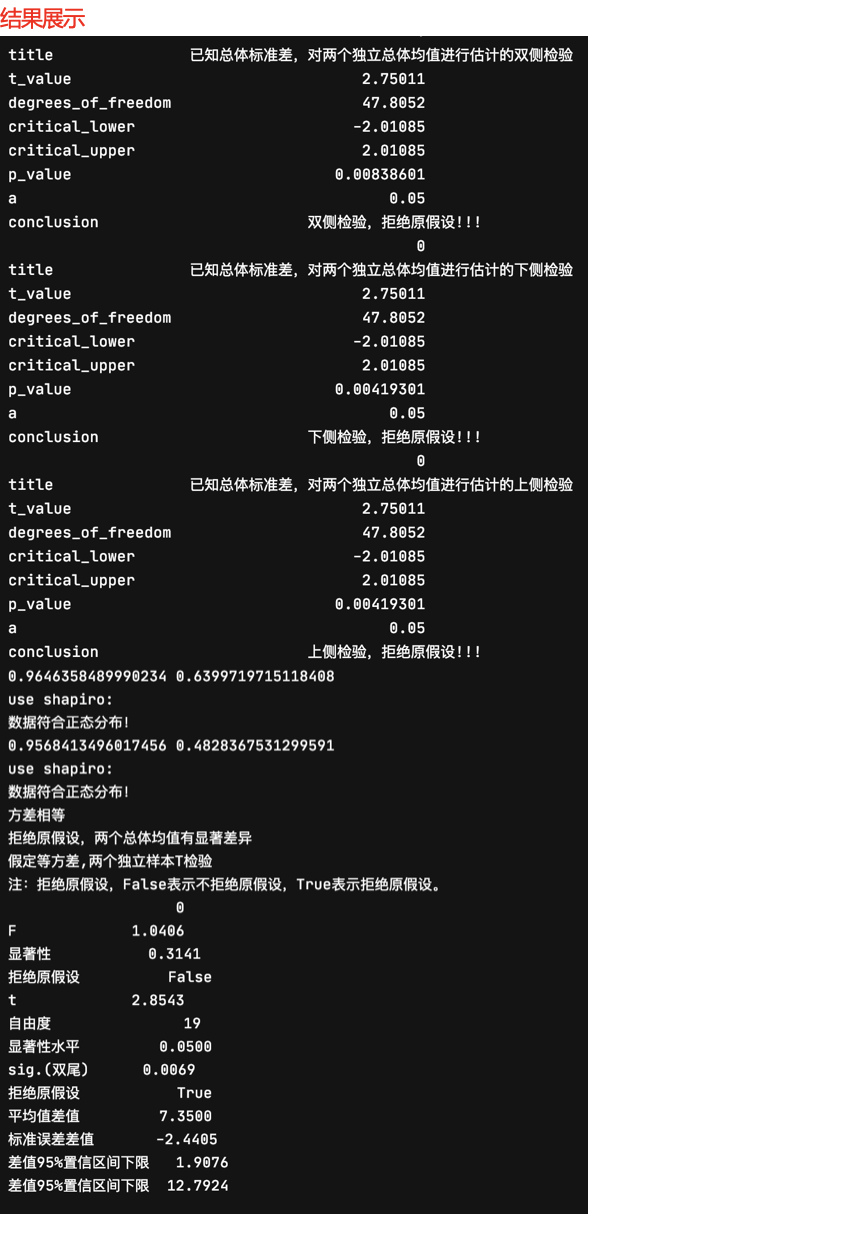
def two_sample_independent_mean_test_t_normal(*args, alpha=0.05):
data = []
mean_diff = args[0].mean() - args[1].mean()
std_diff = args[0].std() - args[1].std()
data_cha = args[0].values - args[1].values
cha_mean = data_cha.mean()
cha_error_mean = data_cha.std() / np.sqrt(len(data_cha)) # 标准误差平均值
cha_df = len(data_cha) - 1 # 自由度
t = stats.t.ppf(alpha / 2, cha_df)
cha_lower = pd.Series([cha_mean - t * cha_error_mean, cha_mean + t * cha_error_mean]).min()
cha_upper = pd.Series([cha_mean - t * cha_error_mean, cha_mean + t * cha_error_mean]).max()
lev, levp = stats.levene(*args) # 输出方差齐性检验的统计量和P值
if levp > alpha:
print('方差相等')
tv, tp = stats.ttest_ind(*args, equal_var=True)
if tp <= alpha:
print('拒绝原假设，两个总体均值有显著差异')
data.append(
["{:.4f}".format(lev), "{:.4f}".format(levp),
"False", "{:.4f}".format(tv), "{:.0f}".format(len(args[0]) - 1),
"{:.4f}".format(alpha),
"{:.4f}".format(tp), "True", "{:.4f}".format(mean_diff),
"{:.4f}".format(std_diff), "{:.4f}".format(cha_lower),
"{:.4f}".format(cha_upper)])
elif tp > alpha:
print('不能拒绝原假设，两个总体均值无显著差异')
data.append(
["{:.4f}".format(lev), "{:.4f}".format(levp),
"False", "{:.4f}".format(tv), "{:.0f}".format(len(args[0]) - 1),
"{:.4f}".format(alpha),
"{:.4f}".format(tp), "False", "{:.4f}".format(mean_diff),
"{:.4f}".format(std_diff), "{:.4f}".format(cha_lower),
"{:.4f}".format(cha_upper)])
print('假定等方差,两个独立样本T检验')
print('注：拒绝原假设，False表示不拒绝原假设，True表示拒绝原假设。')
return pd.DataFrame(data,columns=["F", "显著性", "拒绝原假设", "t", "自由度","显著性水平",
"sig.(双尾)", "拒绝原假设", "平均值差值", "标准误差差值",
"差值{:.0%}置信区间下限".format(1 - alpha), "差值{:.0%}置信区间下限".format(1 - alpha)]
# "remarks": "注：拒绝原假设，False表示不拒绝原假设，True表示拒绝原假设。"
).T
elif levp <= alpha:
print('方差不相等')
tv, tp = stats.ttest_ind(*args, equal_var=False)
if tp <= alpha:
print('拒绝原假设，两个总体均值有显著差异')
data.append(
["{:.4f}".format(lev), "{:.4f}".format(levp),
"True", "{:.4f}".format(tv), "{:.0f}".format(len(args[0]) - 1),
"{:.4f}".format(alpha),
"{:.4f}".format(tp), "True", "{:.4f}".format(mean_diff),
"{:.4f}".format(std_diff), "{:.4f}".format(cha_lower),
"{:.4f}".format(cha_upper)])
elif tp > alpha:
print('不能拒绝原假设，两个总体均值无显著差异')
data.append(
["{:.4f}".format(lev), "{:.4f}".format(levp),
"True", "{:.4f}".format(tv), "{:.0f}".format(len(args[0]) - 1),
"{:.4f}".format(alpha),
"{:.4f}".format(tp), "False", "{:.4f}".format(mean_diff),
"{:.4f}".format(std_diff), "{:.4f}".format(cha_lower),
"{:.4f}".format(cha_upper)])
print('不假定等方差,两个独立样本T检验')
print('注：拒绝原假设，False表示不拒绝原假设，True表示拒绝原假设。')
return pd.DataFrame(data, columns = ["F", "显著性", "拒绝原假设", "t", "自由度","显著性水平",
"sig.(双尾)", "拒绝原假设", "平均值差值", "标准误差差值",
"差值{:.0%}置信区间下限".format(1 - alpha), "差值{:.0%}置信区间下限".format(1 - alpha)]
).T
if __name__ == '__main__':
# 样本量1：28
# 样本量2：22
# 样本均值1：1025
# 样本均值2：910
# 显著性水平：0.05
# 总体均值差的假设值：0
# 样本标准差1：150
# 样本标准差2：125
conclusion = two_sample_independent_mean_test_t(28, 22, 1025, 918, 0.05, 0, 150, 125, 'two')
print(conclusion)
# 样本量1：28
# 样本量2：22
# 样本均值1：1025
# 样本均值2：910
# 显著性水平：0.05
# 总体均值差的假设值：0
# 样本标准差1：150
# 样本标准差2：125
conclusion_downside = two_sample_independent_mean_test_t(28, 22, 1025, 918, 0.05, 0, 150, 125, 'downside')
print(conclusion_downside)
# 样本量1：28
# 样本量2：22
# 样本均值1：1025
# 样本均值2：910
# 显著性水平：0.05
# 总体均值差的假设值：0
# 样本标准差1：150
# 样本标准差2：125
conclusion_upside = two_sample_independent_mean_test_t(28, 22, 1025, 918, 0.05, 0, 150, 125, 'upside')
print(conclusion_upside)
data = pd.read_csv('../data/t_two_independent.csv', header=0)
# 1、两个样本量数据可不一样
# 2、方差可不齐
'''
准备数据
'''
group1 = data[data['level'] == 1]['value']
group2 = data[data['level'] == 2]['value']
groups = [group1, group2]
'''
正态性检验
'''
alpha = 0.05
# 正态性检验
NormalTest(groups, alpha=alpha)
# T检验
conclusion_n = two_sample_independent_mean_test_t_normal(*[group1, group2], alpha=alpha)
print(conclusion_n)
import numpy as np
import scipy.stats as stats
import pandas as pd
'''
场景：对两个独立总体比率进行估计，用z检验
'''
def two_sample_independent_ratio_test_z(sample_size1, sample_size2, sample_ratio1, sample_ratio2, alpha, entirety_diff,
tail_type):
"""
接口请求参数:{
"sample_size1": "", # int,第一个样本的样本量
"sample_size2": "", # int,第二个样本的样本量
"sample_ratio1": "", # float,第一个样本的比率
"sample_ratio2": "", # float,第二个样本的比率
"alpha":"", # float,显著性
"entirety_diff":"", # float,两个总体均值差的假设值
"tail_type":"",# str, 上下侧检验分类, two:双侧检验，downside: 下侧检验，upside:上侧检验
:return:
"""
pm = (sample_size1*sample_ratio1 + sample_size2*sample_ratio2)/(sample_size1 + sample_size2)
# z = ((sample_mean1 - sample_mean2) - entirety_diff) / np.sqrt((entirety_std1 * entirety_std1 / sample_size1) + (
# entirety_std2 * entirety_std2 / sample_size2)) # 总体标准差已知时，代入求z值
z = (sample_ratio1 - sample_ratio2)/np.sqrt(pm*(1-pm)*(1/sample_size1 + 1/sample_size2))
p = stats.norm.sf(abs(z)) * 2 # 由z值计算p值,注意这里的绝对值
lower = -stats.norm.ppf(alpha / 2) # 根据显著性求临界值
upper = stats.norm.ppf(alpha / 2) # 根据显著性求临界值
critical_lower = min(lower, upper)
critical_upper = max(lower, upper)
# 双侧检验
if tail_type == 'two':
if ((abs(z) >= abs(critical_lower)) or (abs(z) >= abs(critical_upper))) or (p <= a): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的双侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p,
"a": alpha,
"conclusion": "双侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 下侧检验
elif tail_type == 'downside':
if (z <= critical_lower) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的下侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "下侧检验，不能拒绝原假设!!!"
}, index=[0]).T
# 上侧检验
elif tail_type == 'upside':
if (z >= critical_upper) or (p / 2 <= alpha): # 用临界值法和P值法都可以检验
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，拒绝原假设!!!"
}, index=[0]).T
else:
return pd.DataFrame({
"title": "已知总体标准差，对两个独立总体比率进行估计的上侧检验",
"z_value": z,
"critical_lower": critical_lower,
"critical_upper": critical_upper,
"p_value": p / 2,
"a": alpha,
"conclusion": "上侧检验，不能拒绝原假设!!!"
}, index=[0]).T
if __name__ == '__main__':
# 样本量1：250
# 样本量2：300
# 样本比率1：0.14
# 样本比率2：0.09
# 显著性水平：0.1
# 总体均值差的假设值：0
conclusion = two_sample_independent_ratio_test_z(250, 300, 0.14, 0.09, 0.1, 0, 'two')
print(conclusion)
# 样本量1：250
# 样本量2：300
# 样本比率1：0.14
# 样本比率2：0.09
# 显著性水平：0.1
# 总体均值差的假设值：0
conclusion_downside = two_sample_independent_ratio_test_z(250, 300, 0.14, 0.09, 0.1, 0, 'downside')
print(conclusion_downside)
# 样本量1：250
# 样本量2：300
# 样本比率1：0.14
# 样本比率2：0.09
# 显著性水平：0.1
# 总体均值差的假设值：0
conclusion_upside = two_sample_independent_ratio_test_z(250, 300, 0.14, 0.09, 0.1, 0, 'upside')
print(conclusion_upside)
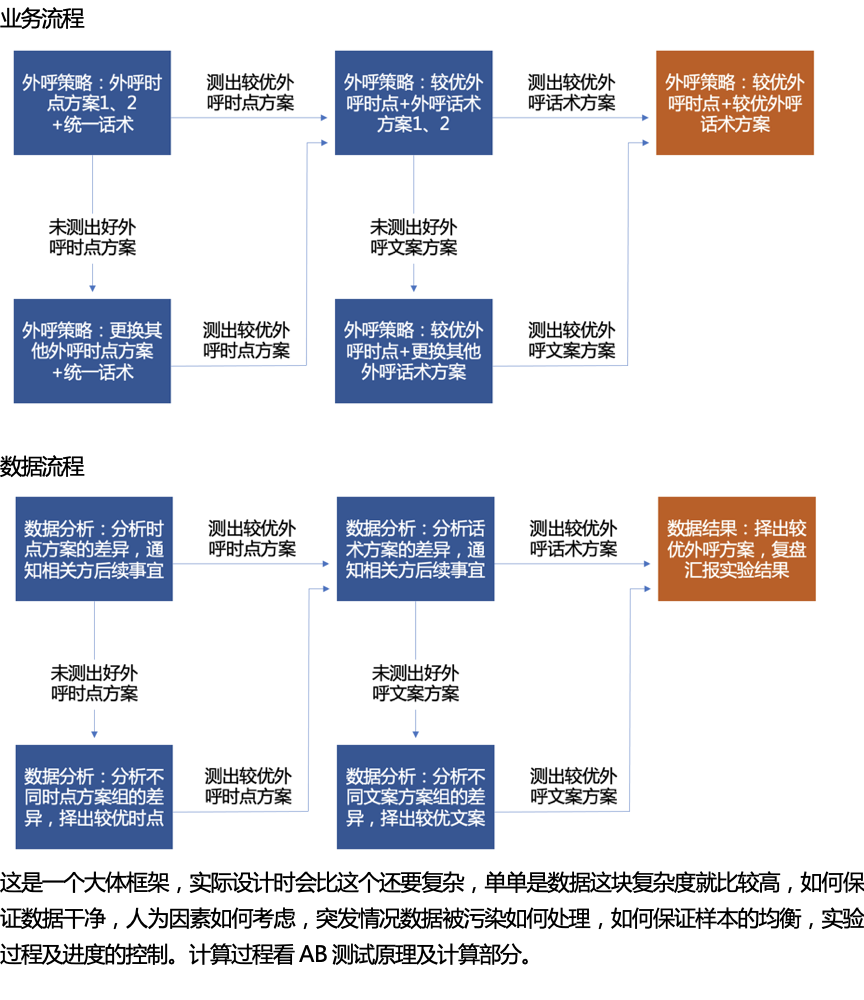
一文搞定AB测试的更多相关文章
- 一文搞定 SonarQube 接入 C#(.NET) 代码质量分析
1. 前言 C#语言接入Sonar代码静态扫描相较于Java.Python来说,相对麻烦一些.Sonar检测C#代码时需要预先编译,而且C#代码必须用MSbuid进行编译,如果需要使用SonarQub ...
- 最强绘图AI：一文搞定Midjourney（附送咒语）
最强绘图AI:一文搞定Midjourney(附送咒语) Midjourney官网:https://www.midjourney.com 简介 Midjourney是目前效果最棒的AI绘图工具.访问Mi ...
- 一文搞定Spring Boot + Vue 项目在Linux Mysql环境的部署（强烈建议收藏）
本文介绍Spring Boot.Vue .Vue Element编写的项目,在Linux下的部署,系统采用Mysql数据库.按照本文进行项目部署,不迷路. 1. 前言 典型的软件开发,经过" ...
- 一文搞定MySQL的事务和隔离级别
一.事务简介 事务是数据库管理系统执行过程中的一个逻辑单位,由一个有限的数据库操作序列构成. 一个数据库事务通常包含了一个序列的对数据库的读/写操作.它的存在包含有以下两个目的: 为数据库操作序列提供 ...
- 一文搞定scrapy爬取众多知名技术博客文章保存到本地数据库，包含：cnblog、csdn、51cto、itpub、jobbole、oschina等
本文旨在通过爬取一系列博客网站技术文章的实践,介绍一下scrapy这个python语言中强大的整站爬虫框架的使用.各位童鞋可不要用来干坏事哦,这些技术博客平台也是为了让我们大家更方便的交流.学习.提高 ...
- 21.SpringCloud实战项目-后台题目类型功能（网关、跨域、路由问题一文搞定）
SpringCloud实战项目全套学习教程连载中 PassJava 学习教程 简介 PassJava-Learning项目是PassJava(佳必过)项目的学习教程.对架构.业务.技术要点进行讲解. ...
- 一文搞定Python正则表达式
本文对正则表达式和 Python 中的 re 模块进行详细讲解 很多人学习python,不知道从何学起.很多人学习python,掌握了基本语法过后,不知道在哪里寻找案例上手.很多已经做案例的人,却不知 ...
- 一文搞定FastDFS分布式文件系统配置与部署
Ubuntu下FastDFS分布式文件系统配置与部署 白宁超 2017年4月15日09:11:52 摘要: FastDFS是一个开源的轻量级分布式文件系统,功能包括:文件存储.文件同步.文件访问(文件 ...
- 工具分享：GitHub的克隆工具Cl0neMast3r，轻松搞定各种测试
GitHub,相信大家并不陌生,咱搞技术的应该都会用到它,GitHub主要是进行代码工具的存储.下载等工作.今天介绍一款让我们操作GitHub相关工作变的更简单的工具, GitHub的克隆工具. Cl ...
- 一文搞定Flask
Flask 一 .Flask简介 Flask是一个基于Python开发并且依赖jinja2模板和Werkzeug WSGI服务的一个微型框架,对于Werkzeug本质是Socket服务端,其用于接收h ...
随机推荐
- DVWA靶场学习
暴力破解Brute Force low 输入密码就正常抓包放字典破解得了 uploading-image-528180.png medium 同样的操作发现响应速度变慢了,但是还是能暴力破解,不多说了 ...
- SpringBoot应用调用Linkis进行任务调度执行SQl；进行数据质量分析
基于Linkis的Rest-API调用任务 官网示例:"https://linkis.apache.org/zh-CN/docs/1.3.2/api/linkis-task-operator ...
- Docker 运行命令
停止所有的容器 docker stop $(docker ps -aq) 启动所有的容器 docker start $(docker ps -aq) 停止容器 docker stop <容器Na ...
- jupyterhub nginx proxy pass----ipv6转ipv4实现内网穿透
jupyterhub 很多人应该已经对jupyter和notebook已经有所了解了.如果是多人共享服务器的话,就需要用到jupyter的多用户版本jupyterhub.jupyterhub架构如图所 ...
- MQ 如何保证数据一致性？
前言 上个月,我们有个电商系统出了个灵异事件:用户支付成功了,但订单状态死活不改成"已发货". 折腾了半天才定位到问题:订单服务的MQ消息,像人间蒸发一样消失了. 这个Bug让我明 ...
- 应急响应 - Linux基础篇
一.Linux应急响应流程 数据备份:所有涉及到分析以及证据的材料都需要提前进行备份,这样也方便之后还有分析人员或者防止数据被篡改或者覆盖. 备份用户信息文件 cat /etc/passwd > ...
- KGDB调试Linux内核与模块
前言 内核 5.10 版本 openEuler 使用 yum install 下载了源码,并且通过两个 VMware 虚拟机进行调试 ubuntu 直接使用 git 拉取了https://kernel ...
- ThreadLocal 内存泄漏原因和解决方法
一.ThreadLocal 内存泄漏的原因 ThreadLocal 的内存泄漏问题主要与其底层实现 ThreadLocalMap 的结构和垃圾回收机制有关.以下是核心原因: 1.ThreadLocal ...
- 从零实现富文本编辑器#2-基于MVC模式的编辑器架构设计
在先前的规划中我们是需要实现MVC架构的编辑器,将应用程序分为控制器.模型.视图三个核心组件,通过控制器执行命令时会修改当前的数据模型,进而表现到视图的渲染上.简单来说就是构建一个描述文档结构与内容的 ...
- python-pandas提取网页内tables（表格类型）数据
比如,下面网页里大学排行的数据 分析这个页面,表格内的数据是包裹在tables里的 这样就可以使用pandas对数据进行提取并且导出成csv文件,具体代码很简单 import pandas as pd ...