深入浅出了解生成模型-4：一致性模型（consistency model）

更加好的排版: https://www.big-yellow-j.top/posts/2025/06/17/CM.html

前面已经介绍了扩散模型，在最后的结论里面提到一点：扩散模型往往需要多步才能生成较为满意的图像。不过现在有一种新的方式来加速（旨在通过少数迭代步骤）生成图像：一致性模型（consistency model），因此这里主要是介绍一致性模型（consistency model）基本原理以及代码实践，值得注意的是本文不会过多解释数学原理，数学原理推导可以参考：

介绍一致性模型之前需要了解几个知识：在传统的扩散模型中无论是加噪还是解噪过程都是随机的，在论文^[1]中（也就是CM作者宋博士的另外一篇论文）将这个随机过程（也就是随机微分方程SDE）转化成“固定的”过程（也就是常微分方程ODE），只有过程可控才能保证下面公式成立。

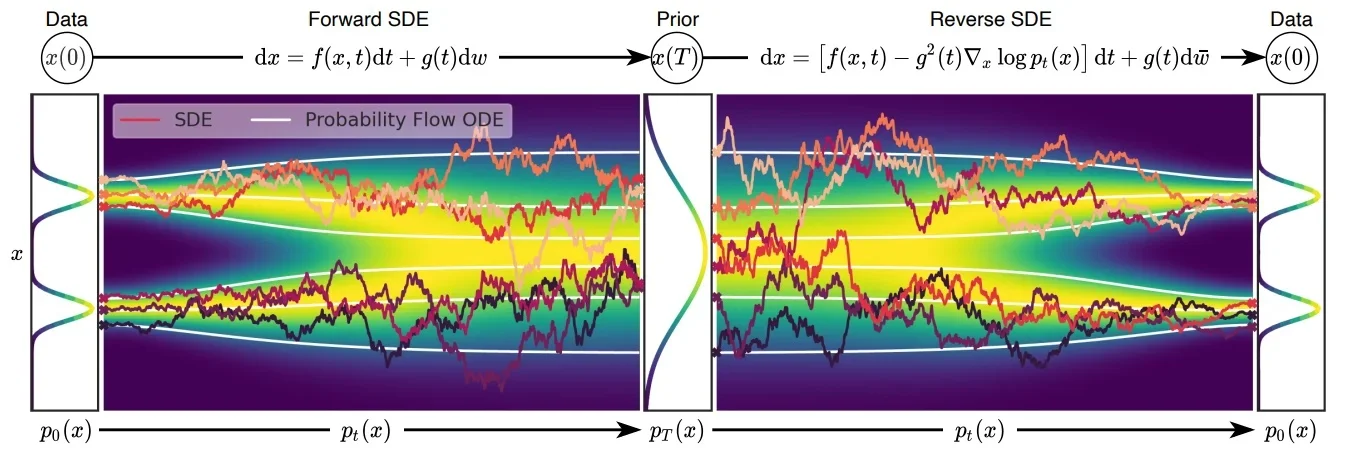
一致性模型（Consistency Model）

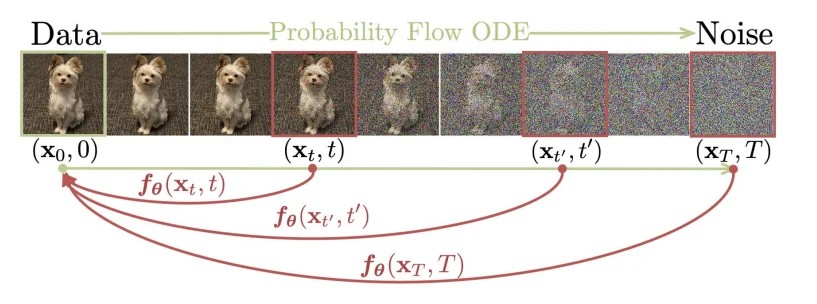
其中ODE（常微分方程），在传统的扩散模型（Diffusion Models, DM）中，前向过程是从原始图像 $x_0$开始，不断添加噪声，经过 $T$步得到高斯噪声图像 $x_T$。反向过程（如 DDPM）通常通过训练一个逐步去噪的模型，将 $x_T$逐步还原为 $x_0$ ，每一步估计一个中间状态，因此推理成本高（需迭代 T 步）。而在 Consistency Models（CM） 中，模型训练时引入了 Consistency Regularization，使得模型在不同的时间步 $t$都能一致地预测干净图像。这样在推理时，无需迭代多步，而是可以通过一个单一函数$f(x ,t)$ 直接将任意噪声图像$x_t$ 还原为目标图像$x_0$ 。这大大减少了推理时间，实现了一步（或少数几步）生成。

一致性模型（consistency model）在论文^[2]里面主要是通过使用常微分方程角度出发进行解释的。Consistency Model 在 Diffusion Model 的基础上，新增了一个约束：从某个样本到某个噪声的加噪轨迹上的每一个点，都可以经过一个函数 $f$ 映射为这条轨迹的起点（也就是通过扩散处理的图像在不同的时间 $t$都可以直接转化为最开始的图像 $x_0$），用数学描述就是：$f:(x_t, t)\rightarrow x_\epsilon$，换言之就是需要满足： $f(x_t,t)=f(x_{t^\prime},t^\prime)$ 其中 $t,t^\prime \in [\epsilon,T]$，正如论文里面的图片描述：

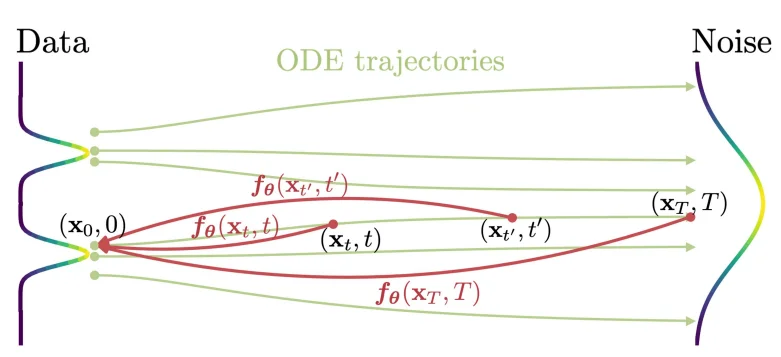
要满足上面的计算关系，作者在论文里面定义如下的等式关系：

\[f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)
\]

其中等式需要满足：$c_{skip}(\epsilon)=1,c_{out}(\epsilon)=0$ （$c_{skip}(t)=\frac{\sigma_{data}^2}{(t- \epsilon)^2+ \sigma_{data}^2}$， $c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{\sigma_{data}^2+ t^2}}$），随着解噪过程（时间从：$T \rightarrow \epsilon$ 其中 $c_{skip}$ 的值逐渐增大，也就是当前的解噪图像占比权重增加），其中我的 $F_\theta$ 就是我们的神经网络模型（比如Unet）。既然使用了神经网络那么必定就需要设计一个损失函数，在论文里面作者设计的损失函数为：两个时间步之间生成得到的图像距离通过最小化这个值（比如说 $\Vert x_{t+1} - x_t \Vert_2$）来优化模型参数。作者对于模型训练给出两种训练方式

直接通过蒸馏模型进行优化

通过直接蒸馏的方式对模型参数进行优化，其中设计的损失函数为：

\[\mathcal{L}_{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-;\phi) = \mathbb{E}[\lambda(t_n)d(\boldsymbol{f}_{\boldsymbol{\theta}}(\mathbf{x}_{t_{n+1}},t_{n+1}),\boldsymbol{f}_{\boldsymbol{\theta}^-}(\hat{\mathbf{x}}_{t_n}^{\boldsymbol{\phi}},t_n))]
\]

其中 $d$代表距离（比如$l_1$或者 $l_2$）对于上面公式中几个参数：$\theta, \theta^-$，其中 $\hat{x}_{t_n}^\phi$ 代表的是一个预训练的 score model。虽然在CM中损失函数设计上一下子又3个模型，但是实际训练过程中更新的只有一个参数：$\theta$。另外一个参数是直接通过：$\theta^- \leftarrow \mu \theta^-+ (1-\mu \theta) $ 通过指数滑动平均方式进行训练。而另外一个参数 $\phi$是一个确定的函数直接通过ODE solver来进行计算得到，比如在论文^[3]的使用的欧拉求解法：

\[\hat{x}_{t_n}^\phi= x_{t_{n+1}}- (t_n- t_{n+1})t_{n+1}\nabla_{x_{t_{n+1}}}\log p_{t_{n+1}}(x_{t_{n+1}})
\]

欧拉法： $y_{n+1}= y_n+h*f(t_n, y_n)$ 其中h代表时间步长，f代表当前导数估计。不过值得进一步了解的是，在DL中大部分函数都是直接通过神经网络进行“估算的”，也就是说对于上面的 $\nabla_{x_{t_{n+1}}}\log p_{t_{n+1}} \textcolor{red}{≈} s_\theta(x_{t_{n+1}},t_{n+1})$ 其中 $s_\theta$代表的是训练好的去噪网络。

那么这样一来整个过程就变成了：

回顾整个过程（直接借鉴上面的流程图），算法比较简单（只不过背后的数学原理蛮复杂），简单描述上面过程就是：对于输入图片通过加噪处理之后得到加噪的图像，损失函数设计就是直接通过计算相邻的两步之间的“距离”最小，对于 $x_{t_{n+1}}$ 我们是已经知道的，但是对于当前时间 $t_n$ 是未知的，因此可以直接通过ODE solver的方式去进行估计，而后再去计算loss并且更新参数，对于students模型参数 $\theta$就可以直接通过计算梯度而后进行更新参数，而对于教师模型参数 $\theta^-$ 可以直接可通过EMA进行更新

直接训练模型进行优化

直接训练模型进行优化，其中具体的过程为：

LCM/LCM-Lora

潜在一致性模型（Latent Consistency Model）^[4]以及LCM-Lora^[5]（LCM的Lora优微调）通过再latent space中使用一致性模型（stable diffusion model通过VAE将图像进行压缩到latent sapce而后通过DF模型训练并且最后再通过VAE decoder输出），在LCM中主要提出两点：

1、Skipping-Step：因为在最开始的CM中计算两个相邻的时间步之间的loss由于时间步过于接近，就会导致loss很小，因此通过跳步解决这个问题，这样loss就会变成：$d(f(x_{t_{n+\textcolor{red}{k}}}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, t_n))$。

2、引入Classifier-free guidance (CFG) 那么整个loss计算就会变成：$d(f(x_{t_{n+\textcolor{red}{k}}}, \textcolor{red}{w}+ \textcolor{red}{c}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, \textcolor{red}{w}+ \textcolor{red}{c}+ t_n))$，公式中c代表文本，对于CFG而言其实就是一个改进的ODE solver（见下面算法流程中的蓝色部分）

对于LCD算法流程，其中蓝色部分为LCM所修改的内容：

对于最后得到的实验结果分析：

不同的k对结果的影响

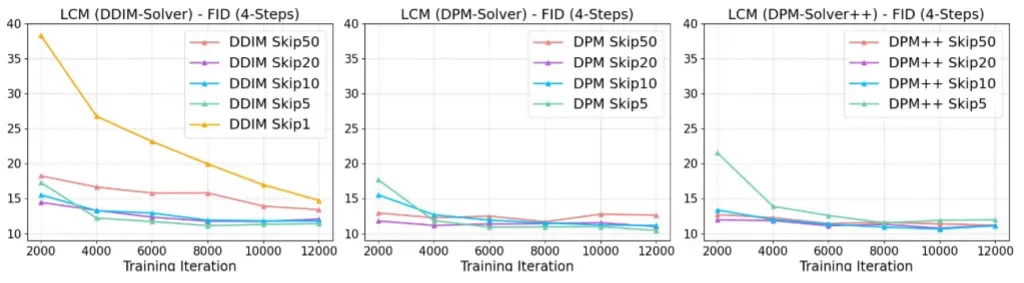
在DPM-solver++和DPM-Solver中基本只需要 2000 步迭代，LCM 4 步采样的 FID 就已经基本收敛了

不同的Guidance Scale对结果的影响

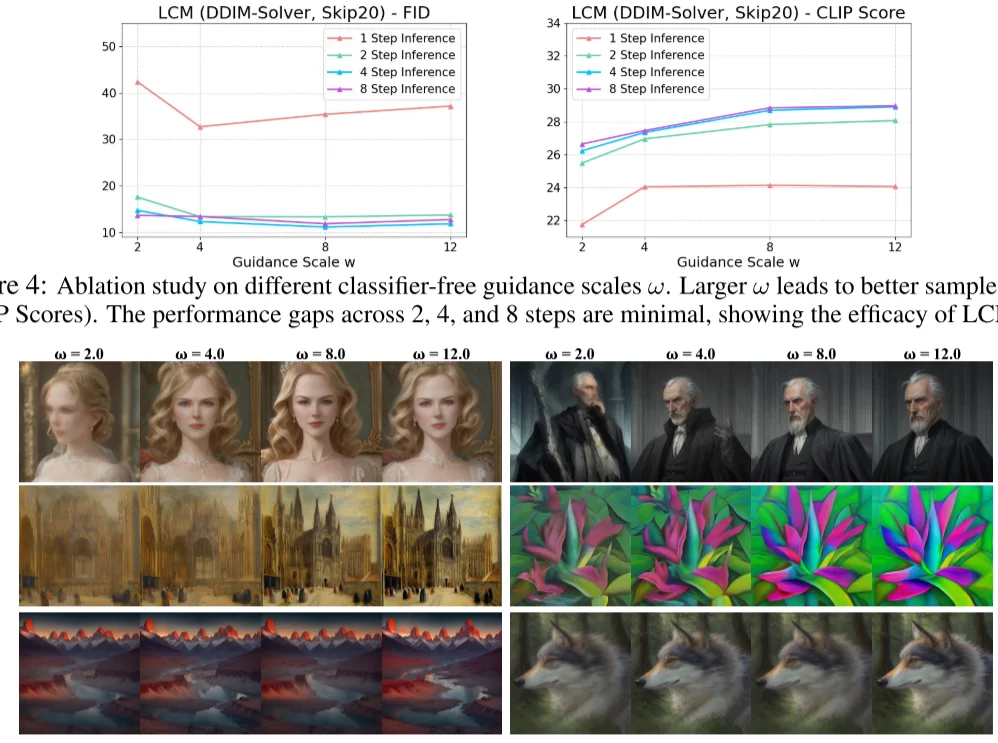
LCM 作者用不同 LCM 的迭代次数与不同 Guidance Scale 做了对比。发现 $w$ 增加有助于提升 CLIP Score，但是损失了 FID 指标（即多样性）的表现。另外，LCM 迭代次数为 2、4、8 时，CLIP Score 和 FID 相差都不大，说明了 LCM 的蒸馏性能确实非常强悍，两步前向的效果可能都足够好了，只是一步前向的结果还差些。

总得来说，在LCM中主要是做了如下几点改进：1、使用skipping-step来“拉大”相邻点之间的距离计算；2、改进了ODE solver。

代码操作^[6]

直接阅读最后总结

直接使用diffuser里面给的案例使用LCM/LCM-lora，代码分析如下：

1、时间步处理以及 $c_{skip}$ 和 $c_{out}$

在代码中实现Skipping-Step因此在代码中处理方法为：首先通过DDPM（因为在代码中使用的教师模型是：stable-diffusion-v1-5/stable-diffusion-v1-5 而他使用的就是DDPM方式）而后计算得到topk（1000//30=33），而后通过构建随机索引（通过DDIM采样步：50）从DDIM的time steps（(np.arange(1, ddim_timesteps + 1) * step_ratio).round().astype(np.int64) - 1）中进行索引。而后计算边界缩放：$c_{skip}(t)=\frac{\sigma_{data}^2}{t^2+ \sigma_{data}^2}$， $c_{out}(t)=\frac{t}{\sqrt{\sigma_{data}^2+ t^2}}$

noise_scheduler = DDPMScheduler.from_pretrained(args.pretrained_teacher_model, subfolder="scheduler", revision=args.teacher_revision)

...

topk = noise_scheduler.config.num_train_timesteps // args.num_ddim_timesteps

index = torch.randint(0, args.num_ddim_timesteps, (bsz,), device=latents.device).long()

start_timesteps = solver.ddim_timesteps[index]

timesteps = start_timesteps - topk

timesteps = torch.where(timesteps < 0, torch.zeros_like(timesteps), timesteps)

# 3. Get boundary scalings for start_timesteps and (end) timesteps.

c_skip_start, c_out_start = scalings_for_boundary_conditions(

    start_timesteps, timestep_scaling=args.timestep_scaling_factor

)

c_skip_start, c_out_start = [append_dims(x, latents.ndim) for x in [c_skip_start, c_out_start]]

c_skip, c_out = scalings_for_boundary_conditions(

    timesteps, timestep_scaling=args.timestep_scaling_factor

)

c_skip, c_out = [append_dims(x, latents.ndim) for x in [c_skip, c_out]]

2、加噪、模型处理

图像通过VAE处理之后然后会直接通过noise_scheduler.add_noise处理，最后通过模型预测得到noise_pred，因为加噪过程是 $z_t=\sqrt{\alpha_t}x_0+ \sqrt{1-\alpha_t}\epsilon$ 通过模型得到了 $z_t$因此反推（get_predicted_original_sample）得到加噪前图像 $x_0$，最后的模型预测就是：$f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)$

noise = torch.randn_like(latents)

noisy_model_input = noise_scheduler.add_noise(latents, noise, start_timesteps)

# 5. Sample a random guidance scale w from U[w_min, w_max] and embed it

w = (args.w_max - args.w_min) * torch.rand((bsz,)) + args.w_min

w_embedding = guidance_scale_embedding(w, embedding_dim=time_cond_proj_dim)

w = w.reshape(bsz, 1, 1, 1)

# Move to U-Net device and dtype

w = w.to(device=latents.device, dtype=latents.dtype)

w_embedding = w_embedding.to(device=latents.device, dtype=latents.dtype)

# 6. Prepare prompt embeds and unet_added_conditions

prompt_embeds = encoded_text.pop("prompt_embeds")

# 7. Get online LCM prediction on z_{t_{n + k}} (noisy_model_input), w, c, t_{n + k} (start_timesteps)

noise_pred = unet(

    noisy_model_input,

    start_timesteps,

    timestep_cond=w_embedding,

    encoder_hidden_states=prompt_embeds.float(),

    added_cond_kwargs=encoded_text,

).sample

pred_x_0 = get_predicted_original_sample(

    noise_pred,

    start_timesteps,

    noisy_model_input,

    noise_scheduler.config.prediction_type,

    alpha_schedule,

    sigma_schedule,

)

model_pred = c_skip_start * noisy_model_input + c_out_start * pred_x_0

3、计算CFG、计算loss

因为LCM是一个文本引导的模型，因此在CFG计算中：

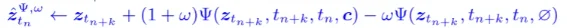
其中就存在计算有条件文本$c$ 和无条件文本 $\emptyset$（直接用空文本uncond_input_ids = tokenizer([""] * args.train_batch_size, return_tensors="pt", padding="max_length", max_length=77).input_ids.to(accelerator.device)uncond_prompt_embeds = text_encoder(uncond_input_ids)[0]进行表示即可）代码。最后计算loss值，更新参数并且通过EMA更新教师模型参数：

with torch.no_grad():

    if torch.backends.mps.is_available():

        autocast_ctx = nullcontext()

    else:

        autocast_ctx = torch.autocast(accelerator.device.type, dtype=weight_dtype)

    with autocast_ctx:

        target_noise_pred = target_unet(

            x_prev.float(),

            timesteps,

            timestep_cond=w_embedding,

            encoder_hidden_states=prompt_embeds.float(),

        ).sample

    pred_x_0 = get_predicted_original_sample(

        target_noise_pred,

        timesteps,

        x_prev,

        noise_scheduler.config.prediction_type,

        alpha_schedule,

        sigma_schedule,

    )

    target = c_skip * x_prev + c_out * pred_x_0

# 10. Calculate loss

if args.loss_type == "l2":

    loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")

elif args.loss_type == "huber":

    loss = torch.mean(

        torch.sqrt((model_pred.float() - target.float()) ** 2 + args.huber_c**2) - args.huber_c

    )

总结

总的来说consistency model作为一种diffusion model生成（区别与DDPM/DDIM）加速操作，在理论上首先将随机生成过程变成“确定”过程，这样一来生成就是确定的，从 $T\rightarrow t_0$ 所有的点都在“一条线”上等式 $f(x_t,t)=f(x_{t^\prime},t^\prime)$ 其中 $t,t^\prime \in [\epsilon,T]$ 成立那么就保证了模型不需要再去不断依靠 $t+1$ 生成内容去推断 $t$时刻内容（具体可以参考算法流程图）。而后续的LCM/LCM-Lora/TCD^[7]则是基于CM的原理进行改进，回顾一下LCM的过程，理解代码（参考Huggingface）操作：

（LCM蒸馏）训练过程中主要使用了3个模型：1、teacher_model；2、unet；3、student_model。其中后面两个模型是相同的，第一个模型可以直接使用训练好的SD模型。

1、首先是构建跳步迭代过程，而后去计算（公式-1） $c_{skip}$和 $c_{out}$以及：$f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)$ 对于其中的$x$ 以及 $F_\theta$ （代码中）分别表示的是$t$时刻模型预测的输出和 $t-1$时刻的噪声图像（加噪反推可以直接计算出来）这样一来就得到（ unet模型计算）：model_pred（对应公式中的：$f_\theta(z_{t_{n+k}},w,c,t_{n+k})$）

2、对于ODE solver计算就和公式-1计算过程相似，只不过需要区分有文本编码和没有文本编码两种，最后得到（这个过程通过教师模型 teacher_model 处理）pred_x0 = cond_pred_x0 + w * (cond_pred_x0 - uncond_pred_x0) 以及 pred_noise = cond_pred_noise + w * (cond_pred_noise - uncond_pred_noise) 而后再通过扩散解噪过程得到$t$时刻的（ODE Solver结果）： x_prev（对应公式中的：$z_{t_n}^{\Psi,w}$）

3、计算loss通过student_model处理 x_prev而后反推得到 pred_x_0再去计算$f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)$（c_skip * x_prev + c_out * pred_x_0）得到target。最后去计算model_pred和 target的loss值，而后去通过EMA更新 student_model参数（通过unet来更新他的参数）

参考