python基础—集合

一、集合（数字，字符串，元组）

1、定义

由不同元素组成的集合，集合中是一组无序排列的哈希值，可以作为字典的key

2、特性

无序，不同元素组成，必须是不可变类型

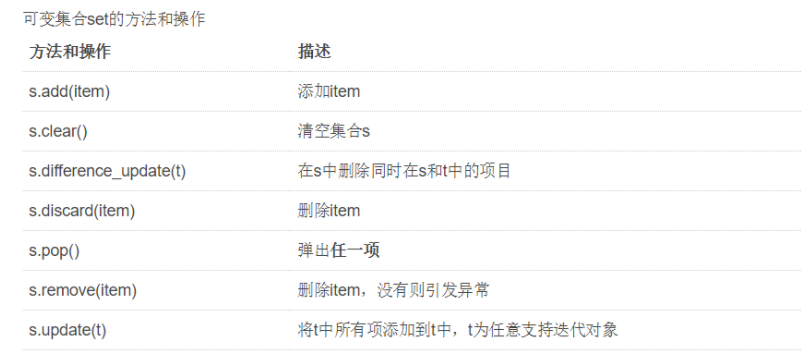
3、set输出与去重

s=set('hello')
s >> {'e', 'h', 'l', 'o'}

4、add添加元素

s = {1,2,3,4,"3"}
s.add(5)
s.add(2)
s >> {1, 2, 3, '3', 4, 5}

5、clear清空集合

s = {1,2,3,4,"3"}
s.clear()
s >> set()

6、copy 拷贝元素

s = {1,2,3,4,"3"}
s1 = s.copy()
s >> [1, 2, 3, 4, '3']
s1 >> [1, 2, 3, 4, '3']
id(s) >>  113879880
id(s1) >>  109192584

7、pop随机删除一个元素

s = {1,2,3,4,"3"}
s.pop() >> '3'
s >> [1,2,3,4]

8、 remove， discard 指定删除  集合中的元素

　 remove 删除不存在元素，会报错。

#使用remove时，如果删除的元素不存在，会报错
s = {1,2,3,4,"3"}
s.remove('sssss')
s >>

ValueError Traceback (most recent call last)
<ipython-input-60-7934dc97039e> in <module>
----> 1 s.remove('ssss')

ValueError: list.remove(x): x not in list

　discard  删除不存在元素，不会报错。

#使用discard时，删除不存在元素，不会报错
s = {1,2,3,4,"3"}
s.discard('sssss')
s >>

{1, 2, 3, 4, '3'}

二、集合的交集，并集，差集

1、交集，两个集合相同的部分

　　intersection　

　　&

p=['lcg','szw','zjw','lcg']
l=['lcg','szw','sb']
p_s=set(p)
l_s=set(l)

p_s >> {'lcg', 'szw', 'zjw'}
l_s >>  {'lcg', 'sb', 'szw'}

#求交集
p_s&l_s >> {'lcg', 'szw'}
p_s.intersection(l_s)  >> 

2、并集，两个集合所有的元素合在一起

　　　union 　　　

　　　　|　

p=['lcg','szw','zjw','lcg']
l=['lcg','szw','sb']
p_s=set(p)
l_s=set(l)

p_s|l_s >> {'lcg', 'sb', 'szw', 'zjw'}
p_s.union(l_s) >> {'lcg', 'sb', 'szw', 'zjw'}

3、差集，两个集合中第一个集合中有，第二个集合中没有的元素

　　　difference

　　　—

p=['lcg','szw','zjw','lcg']
l=['lcg','szw','sb']
p_s=set(p)
l_s=set(l)
p_s-l_s  >>  {'zjw'}
p_s.difference(l_s) >>  {'zjw'}

4、交叉补集，两个集合除去相同元素所得到的集合

　　symmetric_difference

　　^

p=['lcg','szw','zjw','lcg']
l=['lcg','szw','sb']
p_s=set(p)
l_s=set(l)
p_s^l_s  >>  {'sb', 'zjw'}
p_s.symmetric_difference(l_s) >>  {'sb', 'zjw'}

5、求差集后更新原集合

　　difference_update

python_l=['lcg','szw','zjw','lcg']
linux_l=['lcg','szw','sb']
p_s=set(python_l)
l_s=set(linux_l)

p_s.difference_update(l_s)
p_s >>  {'zjw'}

6、判断两集合是否有交集，没有为Ture

　　isdisjoint

s1={1,2,3}
s2={4,5}
s1.isdisjoint(s2)  >> True

7、判断s1是不是s2的子集

　issubset

s1={1,2,}
s2={1,2,3}
s1.issubset(s2)  >> True 

8、判断s1是不是s2的父集

　　issuperset

s1={1,2,3}
s2={1,2,}
s1.issuperset(s2) >> True

9、更新多个值

　　update　

s1={1,2,3}
s1.update([4,5])
s1 >>

{1, 2, 3, 4, 5}

10、frozenset  不可变集合  

　元素一经创建，不可增加、删除和修改。因此没有add、pop、discard、remove和所有以_update结尾的方法。但可以作为左值接受赋值。