redis持久化的方法及对比
1、持久化的作用
redis所有的数据保持在内存中,对数据的更新将异步的保存到磁盘上。
两种方式:

2、RDB
2.1、概念
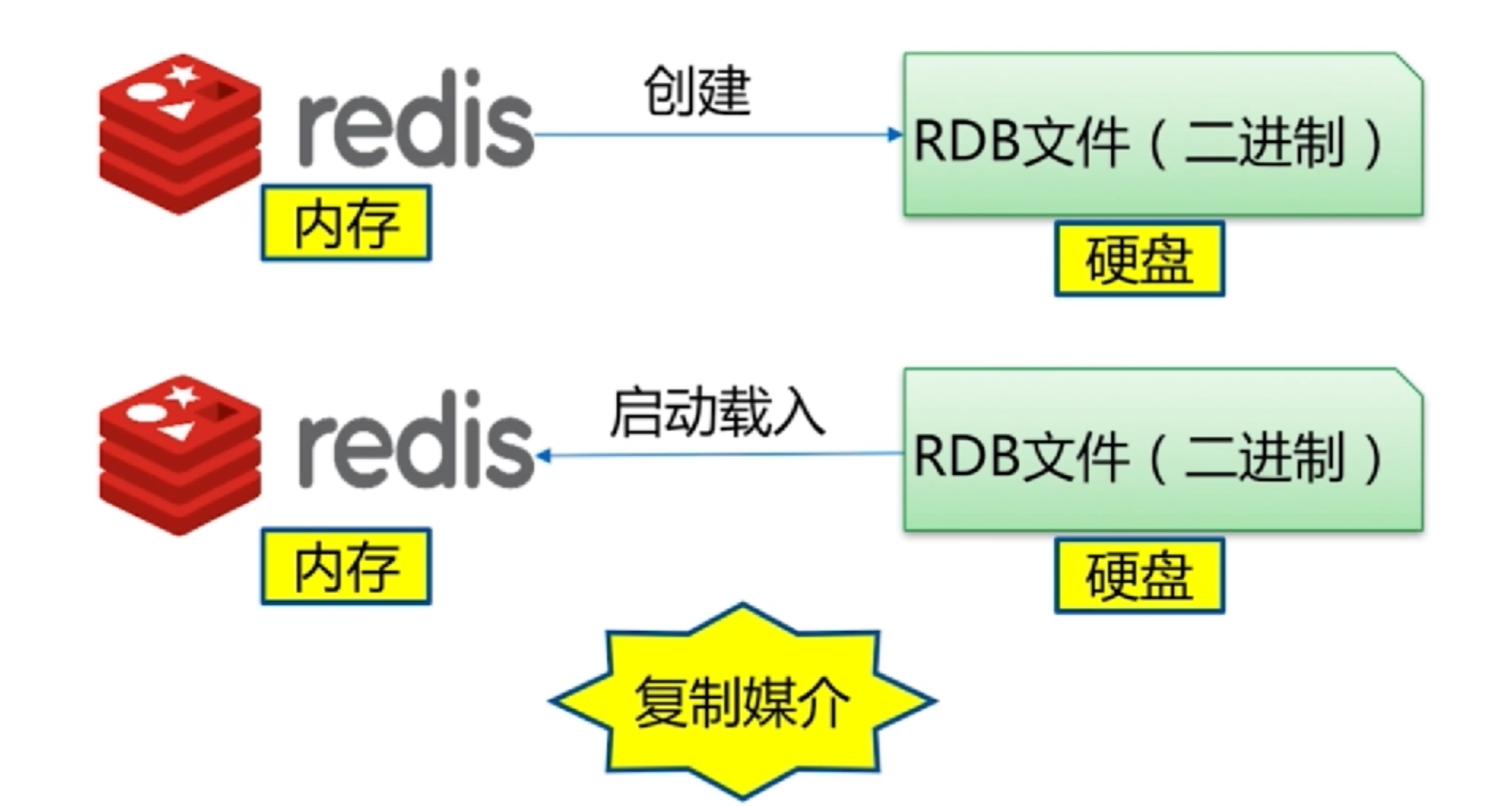
2.2、触发机制
2.2.1、save 同步

因为是同步命令,数据量大的话可能会造成阻塞
文件策略:如果存在老的RDB文件,会用新的替换老的
2.2.2、bgsave 异步
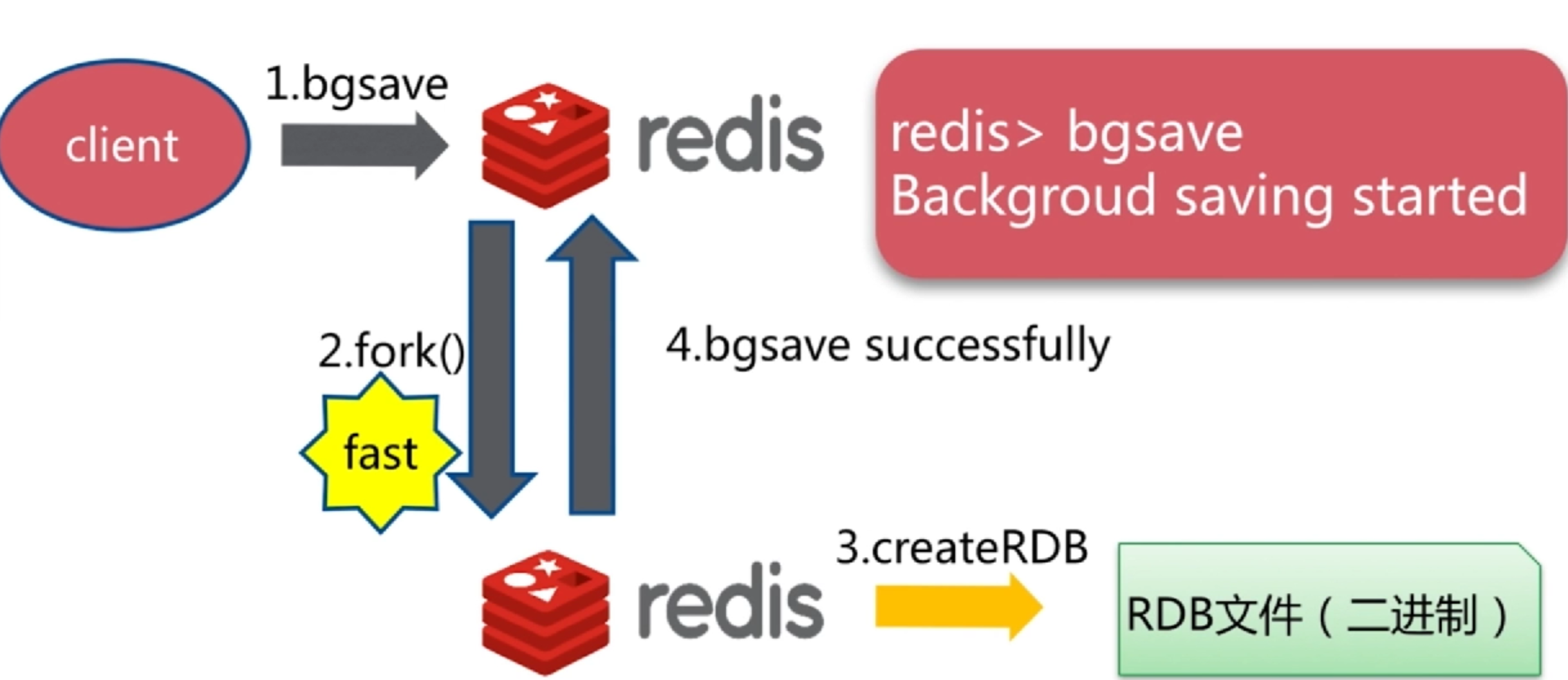
需要linux的fork,很快,不过也有可能会阻塞掉主进程
文件策略同上
2.2.3、自动
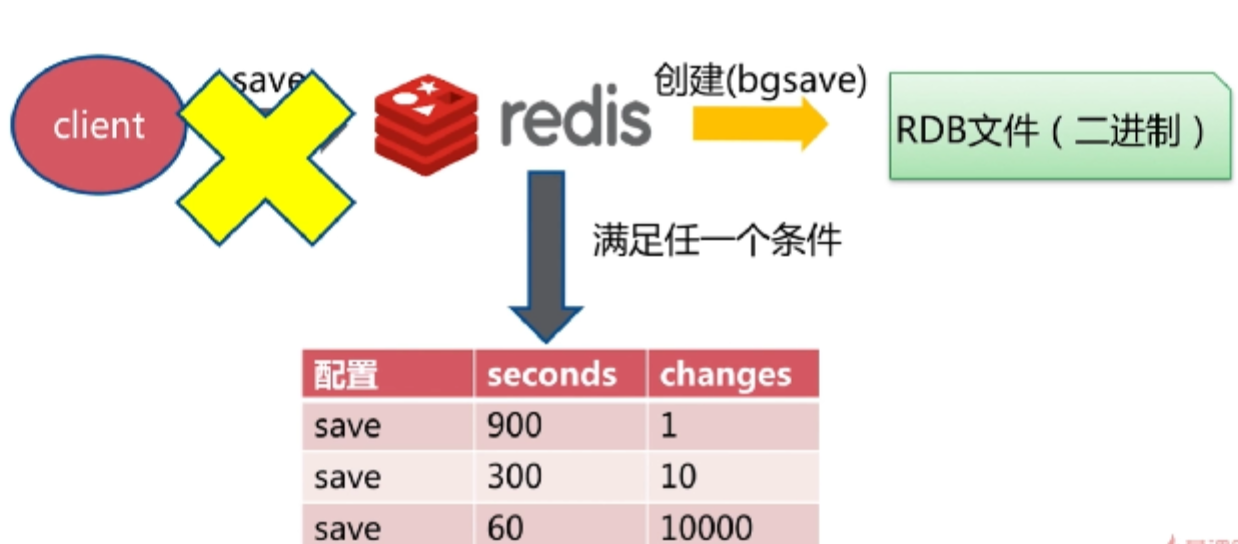
推荐配置:
//满足任一条件就执行
save 900 1
save 300 10
save 60 10000
//文件名加入端口号,以防多redis时覆盖
dbfilename dump-${port}.rdb
//写入目录另外分盘或者是大一点的目录,而不是当前目录
dir /bigdispath
//写入错误时是否停止写入
stop-writes-on-bgsave-error yes
//是否压缩
rdbcompression yes
//是否采用校验模式
rdbchecksum yes
2.3、演示
设置60秒钟改变5次就自动保存
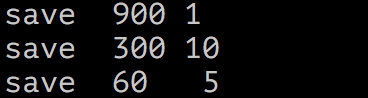
查看日志,自动保存

2.4、问题
耗时耗性能
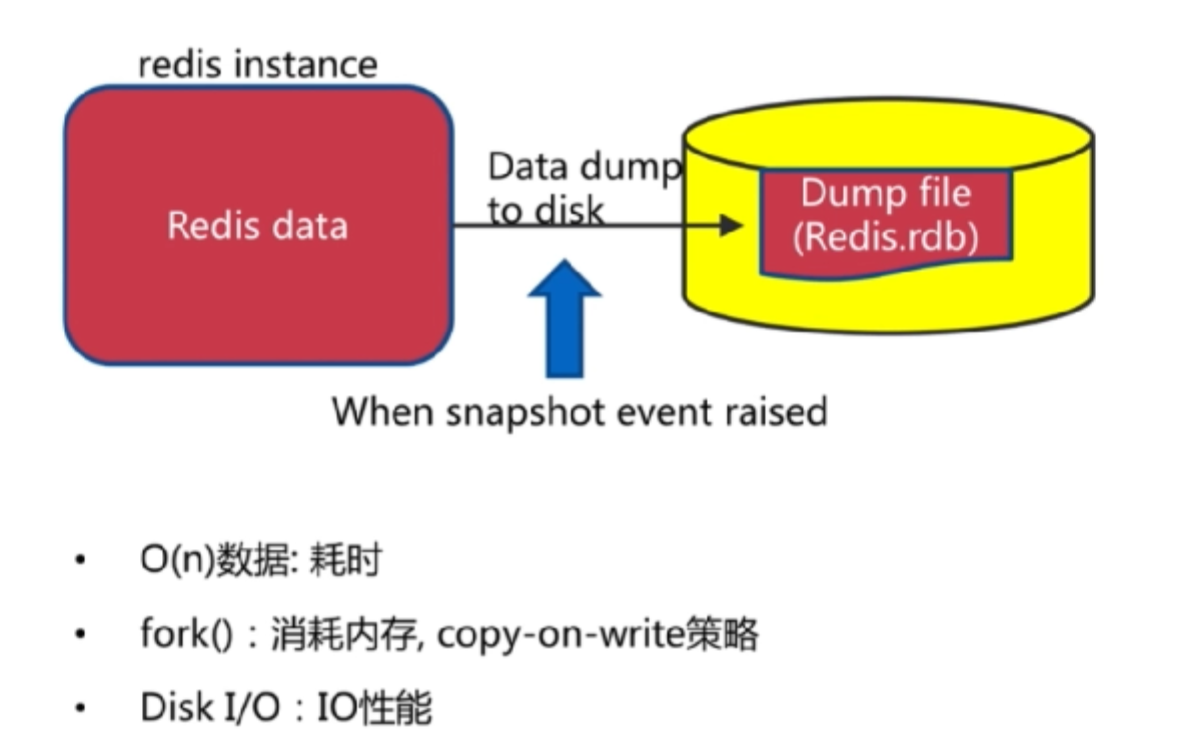
容易丢数据,不可控
3、AOF
3.1、三种策略
always 每次改变数据都存
everysec 每秒存一次
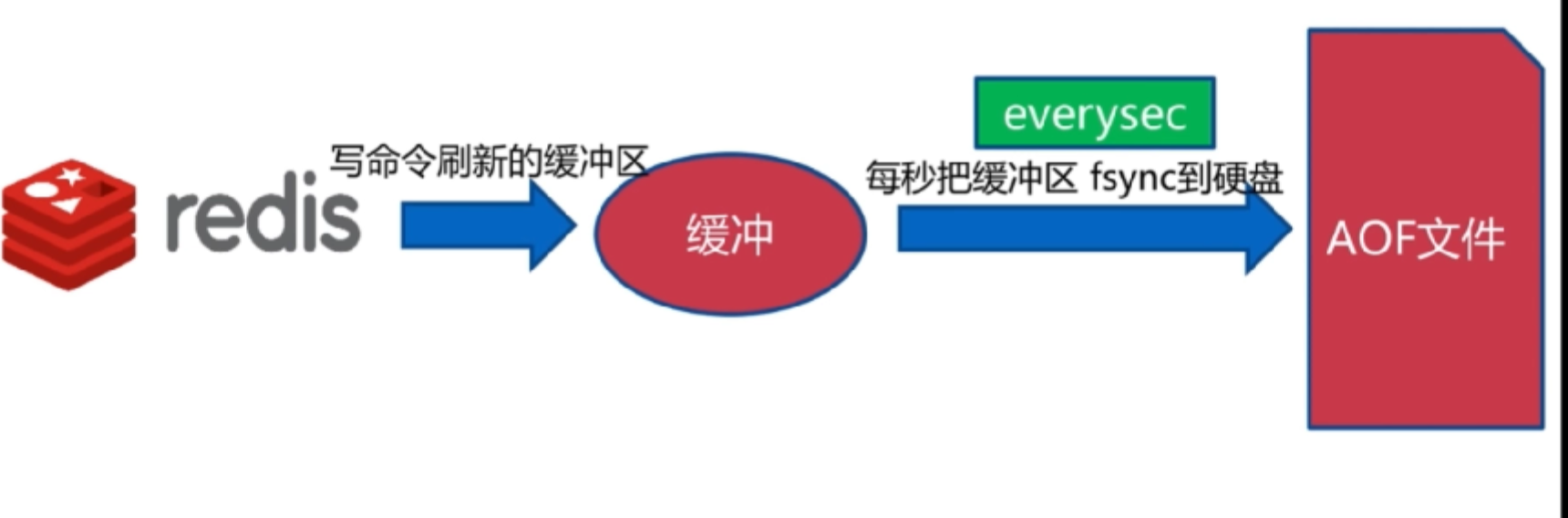
no 操作系统决定
对比
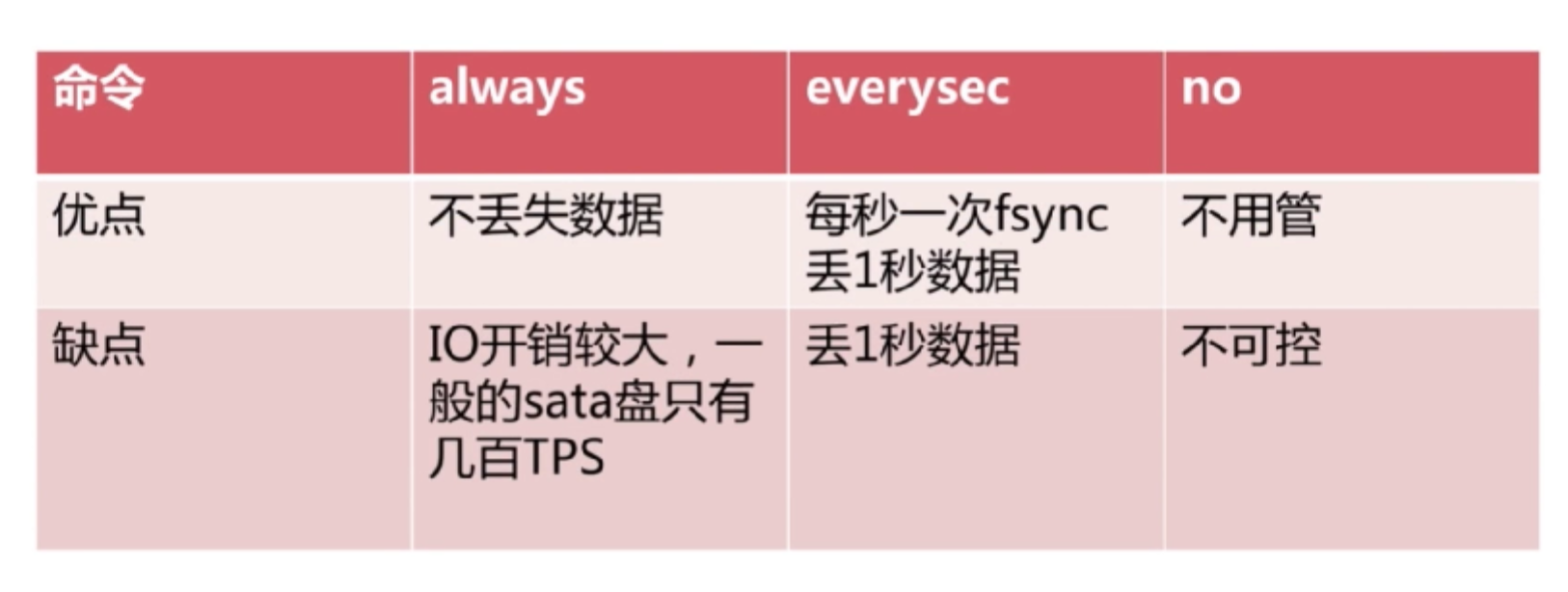
一般使用第二种
AOF重写
自动优化命令、过滤过期数据
AOF重写流程
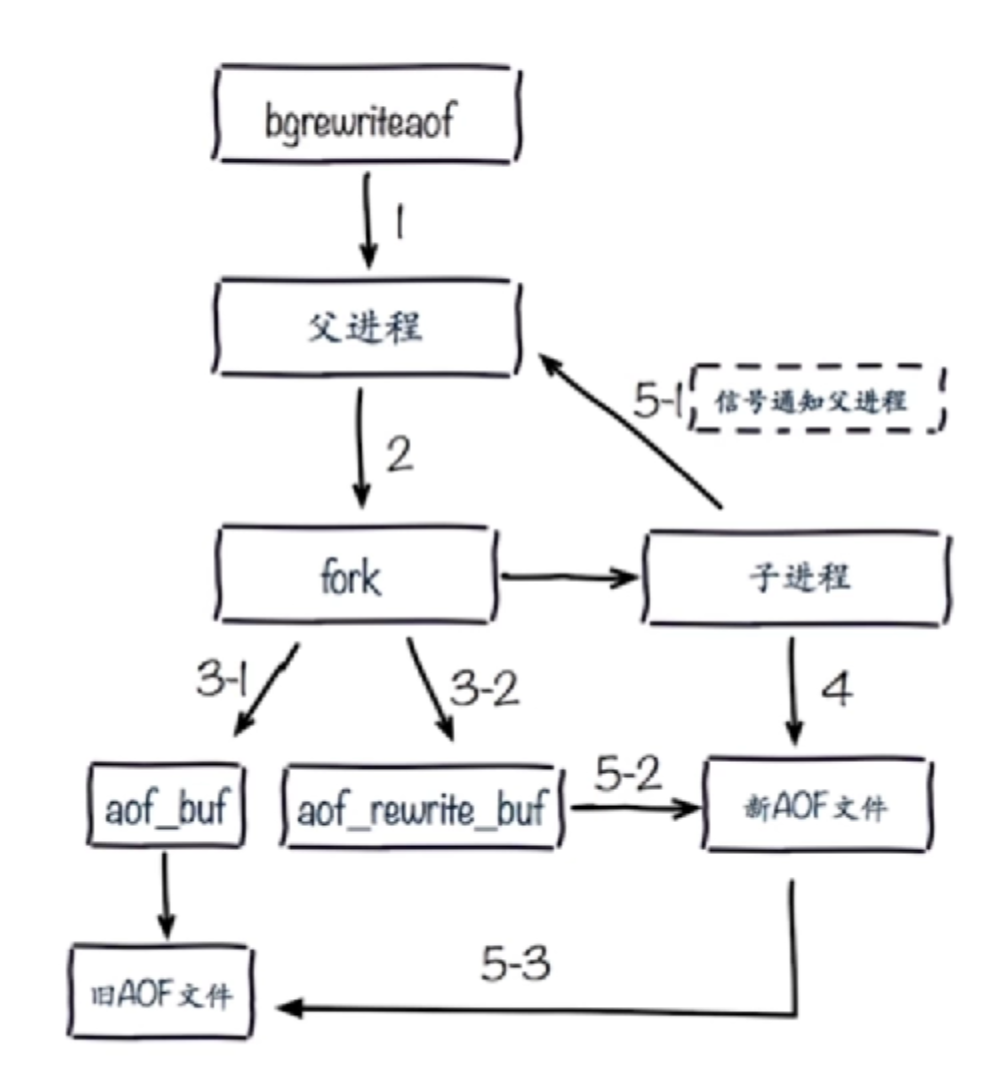
AOF重写作用
减少硬盘占有量,加快恢复速度
实现
bgrewriteaof 异步执行
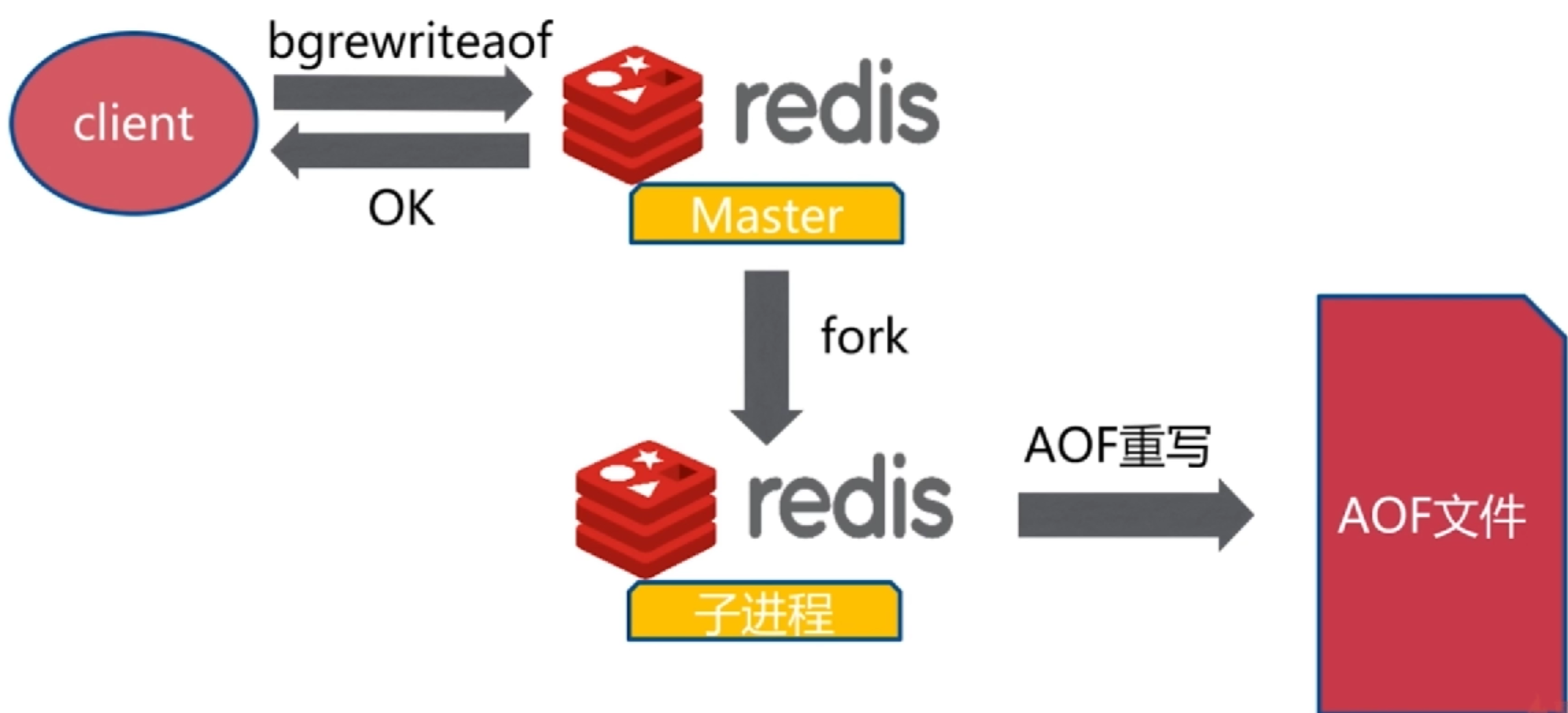
AOF重写配置



4、选择
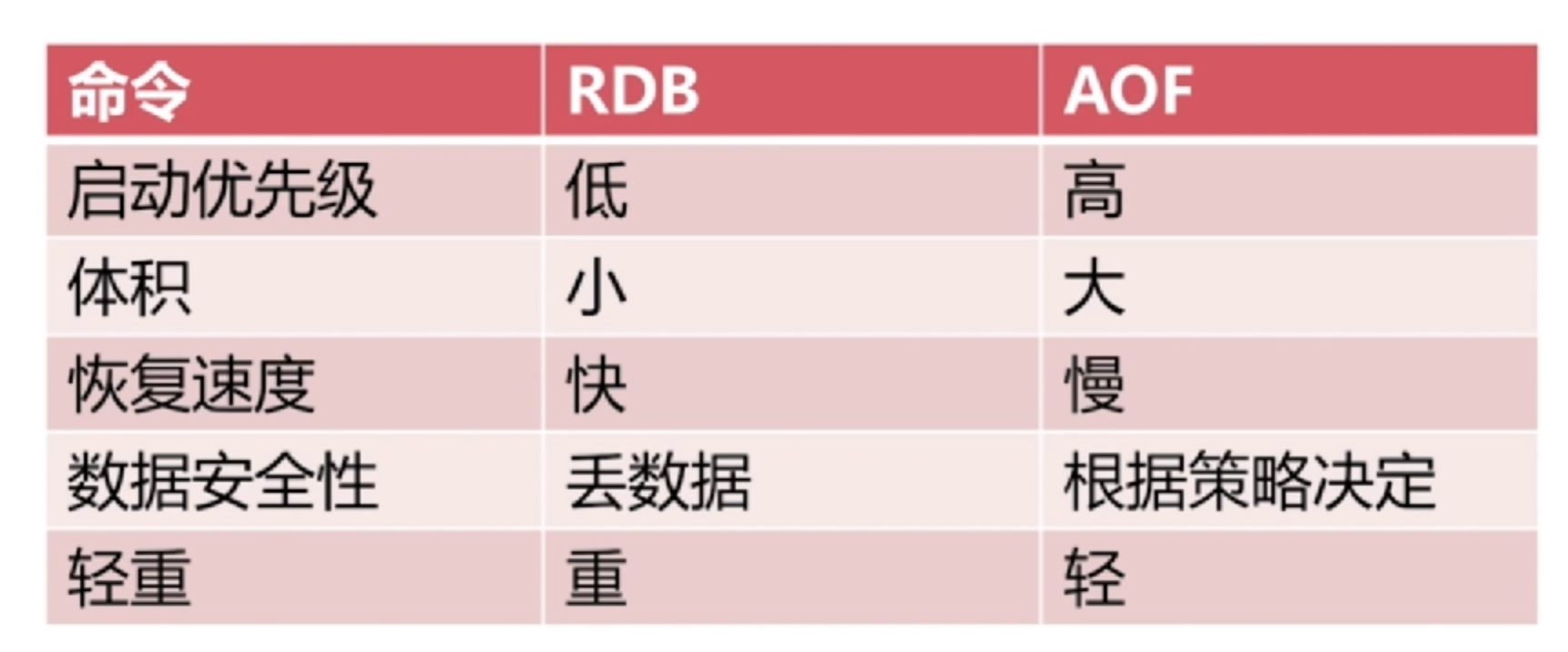

redis持久化的方法及对比的更多相关文章
- Redis 持久化 rdb、Aof对比
一.Redis 简介: Redis是一个开源的.基于内存的数据结构存储器,可以用作数据库.缓存和消息中间件. Redis是一个key-value存储系统.和Memcached类似,它支持存储的valu ...
- Redis持久化AOF和RDB对比
RDB持久化 AOF持久化 全量备份,一次保存整个数据库 增量备份,一次保存一个修改数据库的命令 保存的间隔较长 保存的间隔默认一秒 数据还原速度快 数据还原速度一般 save会阻塞,但bgsave或 ...
- redis持久化那些事(kēng)儿
这是一篇包含了介绍性质和吐槽性质的日志.主要介绍一下我学习redis持久化时候被坑的经历.redis的使用介绍现在没有打算写,因为比较多,以我如此懒的性格...好吧,还是有点这方面想法的,不过一篇博客 ...
- redis持久化方法
1.redis持久化,来自官方说明 如何选择使用哪种持久化方式? 一般来说, 如果想达到足以媲美 PostgreSQL 的数据安全性, 你应该同时使用两种持久化功能. 如果你非常关心你的数据, 但仍然 ...
- redis持久化RDB和AOF
Redis 持久化: 提供了多种不同级别的持久化方式:一种是RDB,另一种是AOF. RDB 持久化可以在指定的时间间隔内生成数据集的时间点快照(point-in-time snapshot). AO ...
- redis 持久化与备份策略 【转载】
本文转载自 http://blog.csdn.net/is_zhoufeng/article/details/10210353 持久化(persistence) 本文是 Redis 持久化文档 的中文 ...
- Redis持久化方式的选择
本文将介绍Redis持久化的两种方式:快照持久化和AOF持久化,并对两种方法进行分析和对比,方便在实际中做出选择. 持久化 什么是持久化 Redis所有数据保存在内存中,对数据的更新将异步地保存到磁盘 ...
- 深入Redis持久化
转载:https://segmentfault.com/a/1190000017193732 一.Redis高可用概述 在介绍Redis高可用之前,先说明一下在Redis的语境中高可用的含义. 我们知 ...
- 五、Redis持久化配置
转载:[https://www.cnblogs.com/xingzc/p/5988080.html] Redis提供的持久化机制(RDB和AOF) Redis提供的持久化机制 Redis是一种面向“k ...
随机推荐
- 关于org.springframework.web.filter.CharacterEncodingFilter的学习
介绍 org.springframework.web.filter.CharacterEncodingFilter 这是一个过滤器,是Spring在web请求中定义request和response的编 ...
- ArcGIS Server中创建的两个账户有什么区别
新手常常有这样的疑问: 在安装ArcGIS Server的时候创建的账户和在ArcGIS Server Manager上面创建的账户有什么区别? 解答:前者是是为ArcGIS Server创建的操作系 ...
- BZOJ4590 SHOI2015自动刷题机(二分答案)
二分答案,分别往尽量小的和尽量大的二分即可. #include<iostream> #include<cstdio> #include<cmath> #includ ...
- 【题解】Bzoj2560串珠子
挺强的……容斥+状压DP.首先想到如果可以求出f[k],f[k]代表联通状态为k的情况下的合法方案数,则f[k] = g[k] - 非法方案数.g[k]为总的方案数,这是容易求得的.那么非法方案数我们 ...
- [CF735D]Taxes
题目大意:给你$n$,把它分成若干个数$n_i$,记价值为$\sum_{i=1}^k(\sum_{j|n_i}j-n_i)$(即分成的每个数的约数和(不包括自身)).(以前写的题,不知道为什么没交) ...
- Visio中设置自定义属性的值
ShapeSheet中User-Define Cells中Prompt格. 帮助解释为:为用户定义的单元格指定说明性提示或注释.应用程序自动将提示文本用引号 (" ") 引起来,以 ...
- 闲话JavaScript与Cookies
使用 Cookies 我们已经知道,在 document 对象中有一个 cookie 属性.但是 Cookie 又是什么?"某些 Web 站点在您的硬盘上用很小的文本文件存储了一些信息,这些 ...
- Educational Codeforces Round 54 (Rated for Div. 2) ABCD
A. Minimizing the String time limit per test 1 second memory limit per test 256 megabytes Descriptio ...
- CMDB资产管理系统开发【day26】:02-数据写入待存区
一.资产自动回报数据及个更新流程图 二.表结构注释(NewAssetApprovalZone) class NewAssetApprovalZone(models.Model): "&quo ...
- Vue项目中引入外部文件(css、js、less)
例子中css文件采用bootstrap.css,js文件采用jQuery,less文件用less.less(自定义文件) 步骤一:安装webpack cnpm install webpack -g 步 ...
