HDU 1166 敌兵布阵 树状数组小结（更新）

树状数组(Binary Indexed Tree(BIT), Fenwick Tree)

是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有

元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

这种数据结构（算法）并没有C++和Java的库支持，需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组

和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组

效率要高很多。但使用范围比线段树小（如查询每个区间最小值问题需要线段树）。

分析上面的几组式子可知，当 i 为奇数时，ci=ai ；当 i 为偶数时，就要看 i 的因子中最多有二的多少次幂，

例如，6 的因子中有 2 的一次幂，等于 2 ，所以 c6=a5+a6（由六向前数两个数的和），4 的因子中有 2 的两次幂，等于 4

所以 c4=a1+a2+a3+a4（由四向前数四个数的和）。

(重点操作)定义问题如下：我们有n个盒子，可能的操作为：

1. 修改操作：往第i个盒子增加石子
2. 计算一段区间和：计算第k个盒子到第l个盒子的石子数量(包含第k个和第l个)

原始的解决方案中(即用普通的数组进行存储，box[i]存储第i个盒子装的石子数)， 操作1和操作2的时间复杂度分别是O(1)和O(n)。假如我们进行m次操作，最坏情况下， 即全为第2种操作，时间复杂度为O(n*m)。使用数状数组，它在最坏情况下的时间复杂度也为O(m log n)，但比起RMQ， 它更容易编程实现，并且所需内存空间更少。

下面来对树状数组的基本思想和操作进行阐述：

idx记为BIT（树状数组）的索引，r记为idx的二进制表示中最右边的1后面0的个数(这个r后面还会出现记得它的含义)， 比如idx=1100(即十进制的12)，那么r=2。tree[idx]记为f数组中， 索引从(idx-2^r +1)到idx的所有数的和，包含f[idx-2^r +1]和f[idx]。即： tree[idx]=f[idx-2r +1]+…+f[idx]，对照表1.1和1.2理解和推算一下，你就会一目了然。 我们也可称idx对索引(idx-2^r +1)到索引idx负责(比如表1.2的 8管着1-8,9管着9)。

这里先补充一句。每个整数都能表示为一些2的幂次方的和，比如13，其二进制表示为1101，所以它能表示为： 13 = 2⁰ + 2² + 2³

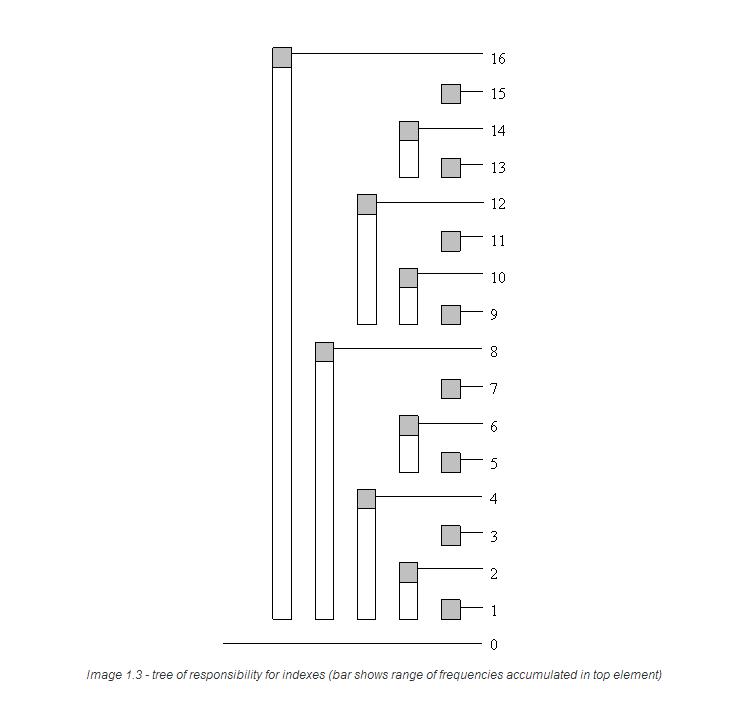
假设我们要得到索引为13的累积频率(即c[13])，在二进制表示中，13=1101。因此(你看一下上面那个图)， 我们是不是可以这样计算：c[1101]=tree[1101]+tree[1100]+tree[1000]  (c[13]=tree[13]（管着f[13]）+tree[12](管着f[9]~f[12])+tree[8](管着f[1]~f[8]))

先观察上面这个式子 c[1101]=tree[1101]+tree[1100]+tree[1000]    有没有发现tree[ ]有上面规律？

分离出最后的1

---

这里先给出上面那个问题的规律；每次分离出最后的1

注意: 最后的1表示一个整数的二进制表示中，从左向右数最后的那个1。

我们知道，对一个数取负等价于对该数的二进制表示取反加1。

num & -num = a1b & a^- 1b = (0…0)1(0…0)

（直接记住！！！）

 int lowbit(int x)

 {

     return x&(-x);

 }

记得刚刚那个r吗(r为idx的二进制表示中最右边的1后面0的个数))两者其实是一样的  即 lowbit(i) ==2^r

读取累积频率

---

给定索引idx，如果我们想获取累积频率即c[idx]（即从1到idx中所有元素的总和），我们只需初始化sum=0, 然后当idx>0时，重复以下操作：sum加上tree[idx], 然后将idx减去相应的lowbit(idx)。

 int read(int idx){

        int sum=;

        while(idx>){

               sum+=tree[idx];

               idx -= lowbit(idx);

        }

        return sum;

 }

为什么可以这么做呢？(重点)

关键是tree数组设计得好。我们知道，tree数组是这么定义的： tree[idx] = f[idx-2^r +1] +…+ f[idx].

上面的程序sum加上tree[idx]后，去掉idx最后的1(比如1100变成1000)，假设变为idx1，

那么有idx1 = idx-2^r (这里的r表示0的个数，上面说过，比如12(1100)去掉12最后的1（即减掉100(4)）变成8(1000)),　

sum接下来加上tree[idx1] = f[idx1-2^r1 +1] +…+ f[idx1] = f[idx1-2^r1 +1] +…+f[idx-2^r ]， 我们可以看到tree[idx1]表达示的最右元素为f[idx-2^r ]，

这与tree[idx]表达式的最左元 素f[idx-2^r +1]无缝地连接了起来。所以，只需要这样操作下去，即可求得f[1]+…+ f[idx]，即c[idx]的结果。

来看一个具体的例子，当idx=13时，初始sum=0:

tree[1101]=f[13]

tree[1100]=f[9]+...+f[12]   (利用上面的解法发现f[12]与f[13]连接在一起)

tree[1000]=f[1]+...+f[8] (利用上面的解法发现f[8]与f[9]连接在一起)

c[1101]=f[1]+...+f[13]=tree[1101]+tree[1100]+tree[1000]

还记得刚才我们讲的。每个整数都能表示为一些2的幂次方的和，比如13，其二进制表示为1101，所以它能表示为：

13 = 2⁰ –>13+ 2²–>12,11,10,9 + 2³–>8,7,6,5,4,3,2,1

改变某个位置的频率并且更新数组

---

当我们改变f数组中的某个值，比如f[idx]，那么tree数组中哪些元素需要改变呢？ 在读取累积频率一节，我们每累加一次tree[idx]，就将idx最后一个1移除， 然后重复该操作。而如果我们改变了f数组，比如f[idx]增加val，我们则需要为当前索引的 tree数组增加val：tree[idx]　+= val。然后idx更新为idx加上其最后的一个1， 当idx不大于MaxVal时，不断重复上面的两个操作。

这里做一个简单地理解，还以13为例，1101，首先它只管1个数，由于没有右边的0，但是它的上面的idx肯定有1后面1个0的那么它就可以分管其自身和它前面一个数，这就是14，就像下面的示例图

1101   13

+    1

1110   14

那么加上一个lowbit(13)其实就是加了一个一倍的最小可以管理的个数

接下来，就应该加上2了，由于1后面一个0，变成16，然后继续加。

其实可以看得出加的是一个相同的个数，让其翻倍，以便让上面管理到它的数组修改值。

 void update(int idx,int val){

        while(idx<=n){

               tree[idx]+=val;

               idx+=lowbit(idx);

        }

 }

下面是hdu1166的树状数组的代码：

需要注意输入输出要用C的输入输出，如果用C++的输入输出流会超时

 /*树状数组模板题*/
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define MAXN 50005
 using namespace std;
 int que[MAXN],c[MAXN];
 char chr[];
 int lowbit(int x)
 {
     return x&(-x);//用来计算a^k中的k
 }
 //实现每个树状数组元素所分管的元素之和的计算
 void create(int n)
 {
     int i,s,j;
     for(i=;i<=n;i++)
     {
         s=lowbit(i);
         for(j=;j<s;j++)//含自身向前推s个
         {
             c[i]=c[i]+que[i-j];
         }
     }
 }
 //求数组的和的算法如下
 int sum(int n)
 {
     int s=;
     while(n>)
     {
         s+=c[n];
         n=n-lowbit(n);
     }
     return s;
 }
 //修改操作，往上修改
 void change(int i,int n,int x)
 {
     while(i<=n)
     {
         c[i]=c[i]+x;
         i=i+lowbit(i);
     }
 }
 int main()
 {
     int t,cas=,i,j,n,x,s,a,b;
     cin>>t;
     while(t--)
     {
         memset(c,,sizeof(c));
         cin>>n;
         for(i=;i<=n;i++)
             scanf("%d",&que[i]);
         create(n);
         cout<<"Case "<<cas++<<":"<<endl;
         while()
         {
             scanf("%s",chr);
             if(!strcmp(chr,"Add"))
             {
                 scanf("%d%d",&j,&x);
                 change(j,n,x);
             }
             else if(!strcmp(chr,"Sub"))
             {
                 scanf("%d%d",&j,&x);
                 change(j,n,-x);
             }
             else if(!strcmp(chr,"Query"))
             {
                 scanf("%d%d",&a,&b);
                 s=sum(b)-sum(a-);
                 printf("%d\n",s);
             }
             else
                 break;
         }
     }
     return ;
 }