HDU2065"红色病毒"问题【指数型母函数】

Problem Description

医学界发现的新病毒因其蔓延速度和Internet上传播的"红色病毒"不相上下,被称为"红色病毒",经研究发现,该病毒及其变种的DNA的一条单链中,胞嘧啶,腺嘧啶均是成对出现的。
现在有一长度为N的字符串,满足一下条件:
(1) 字符串仅由A,B,C,D四个字母组成;
(2) A出现偶数次(也可以不出现);
(3) C出现偶数次(也可以不出现);
计算满足条件的字符串个数.
当N=2时,所有满足条件的字符串有如下6个:BB,BD,DB,DD,AA,CC.
由于这个数据肯能非常庞大,你只要给出最后两位数字即可.

 

Input

每组输入的第一行是一个整数T,表示测试实例的个数,下面是T行数据,每行一个整数N(1<=N<2^64),当T=0时结束.

 

Output

对于每个测试实例,输出字符串个数的最后两位,每组输出后跟一个空行.

 

Sample Input

4
1
4
20
11
3
14
24
6
0

 

Sample Output

Case 1: 2

Case 2: 72

Case 3: 32

Case 4: 0

 

 

Case 1: 56

Case 2: 72

Case 3: 56

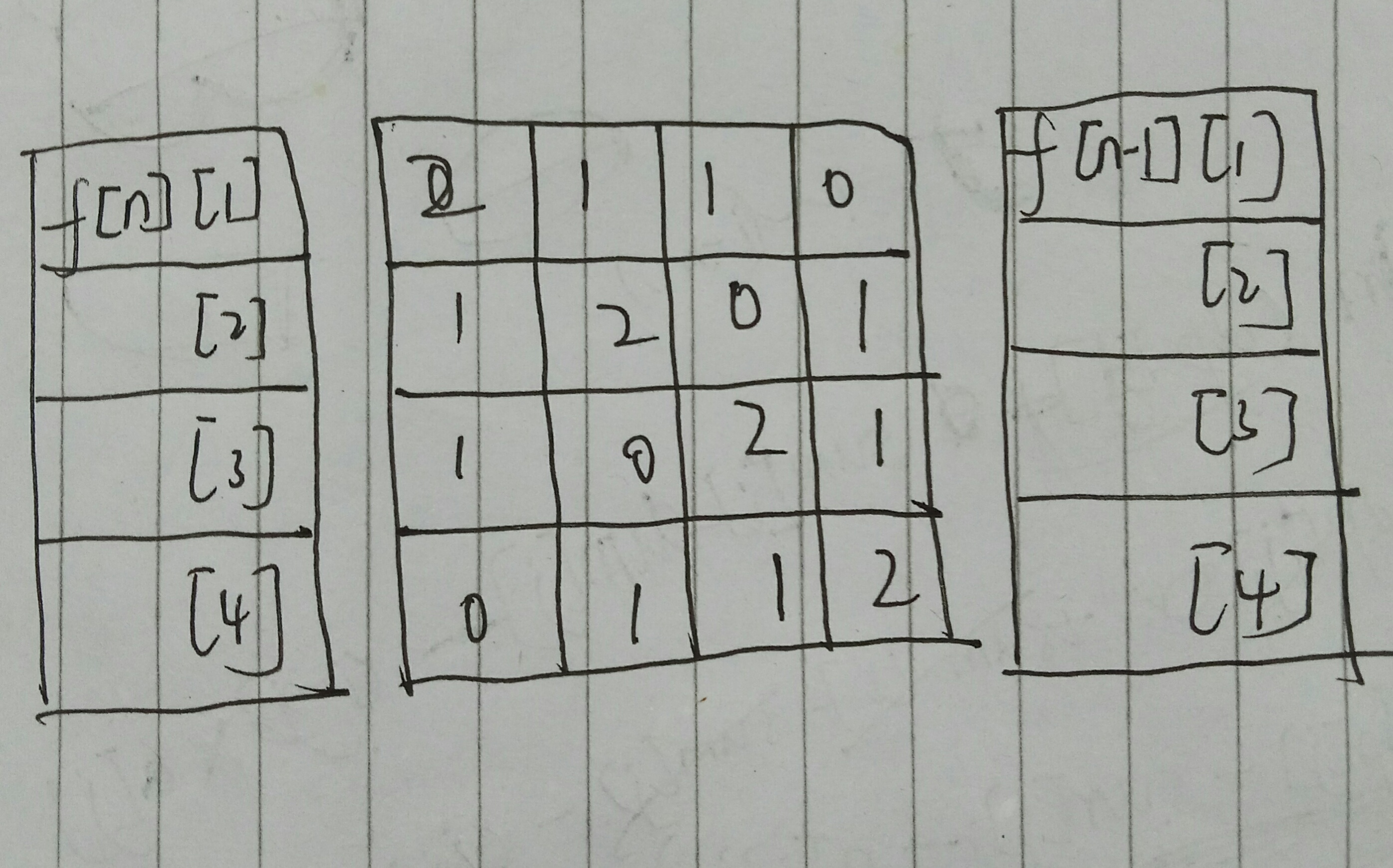
矩阵思路：用f[i][1]表示前i个里面有偶数个A和偶数个C，f[i][2]表示....然后易得。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define LL long long
const int maxn=;
const int Mod=;
struct mat
{
    int m[maxn][maxn];
    mat(){memset(m,,sizeof(m));};
    mat friend operator *(mat a,mat b)
    {
        mat d;
        for(int i=;i<=;i++)
         for(int j=;j<=;j++)
          for(int k=;k<=;k++)
           d.m[i][j]=(d.m[i][j]+a.m[i][k]*b.m[k][j])%Mod;
        return d;
    }
    mat friend operator ^(mat a,LL n)
    {
        mat d;
        for(int i=;i<=;i++) d.m[i][i]=;
        while(n){
            if(n&) d=d*a;
            a=a*a;
            n>>=;
        }
        return d;
    }
};
int main()
{
    int i,Case,T;
    LL n;
    while(~scanf("%d",&T)&&T){
        Case=;
        while(T--){
           scanf("%lld",&n);
           mat b,ans;
           b.m[][]=;b.m[][]=;b.m[][]=;
           b.m[][]=;b.m[][]=;b.m[][]=;
           b.m[][]=;b.m[][]=;b.m[][]=;
           b.m[][]=;b.m[][]=;b.m[][]=;
           ans=b^n;
           printf("Case %d: %d\n",++Case,ans.m[][]);
       }
       printf("\n");
   }
    return ;
}

然而不小心看到其他方法，一下子蒙圈了，QwQ：

方法1，找循环结构，不难想。

方法2，DP，还没有看，多半和循环结构有关。

方法3，指数形母函数，和泰勒公式有关。

高数学了泰勒，我之前也学了母函数，不过比较基础：nmphy的母函数。

然后就翻论文看各种母函数。

后面发现母函数还可以解决【树的计数】问题，因为之前看过Prufer和Cayley 算法，然后就去看母函数来解决树的计数。

树的计数问题。

外文的看不懂，GG。

中文里感觉好的：

http://www.docin.com/p-538824587.html  kb就是kb，大佬！

http://www.docin.com/p-140832665.html  这篇论文和其他论文有相似之处，也有独到之处，还不错。

反正越看越觉得自己数学不够用。

http://ishare.iask.sina.com.cn/f/67448295.html 史老爷，看过他的数学分析的举个手。

学会了高阶母函数再来补充！

2017-11-15

--------------------------------------------------------------分界线就是我----------------------------------------------------------------------

2017-11-20：

感觉母函数很神奇，很强大，用处太多了。

ORZ！！！

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define LL long long
int pow(int a,LL n)
{
    int ans=;
    while(n){
        if(n&) ans*=a;
        ans%=;
        a=a*a%;
        n>>=;
    }
    return ans;
}
int main()
{
    int T,i,j,ans,Case,m;
    LL n;
    while(~scanf("%d",&T)){
        if(T==) return ;
        Case=;
        for(i=;i<=T;i++){
            scanf("%lld",&n);
            printf("Case %d: ",++Case);
            printf("%d\n",(pow(,n-)+pow(,n-))%);
        }
        printf("\n");
    }
    return ;
}

反正就是用这样【简单的公式】就能推出来，所以有时间的伙伴一定要看看母函数。

这里不做解释，自己看书,毕竟我也讲不清楚。