luoguP4151 [WC2011]最大XOR和路径

题意

这题有点神啊。

首先考虑注意这句话：

路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数

也就是说如果出现下面的情况：



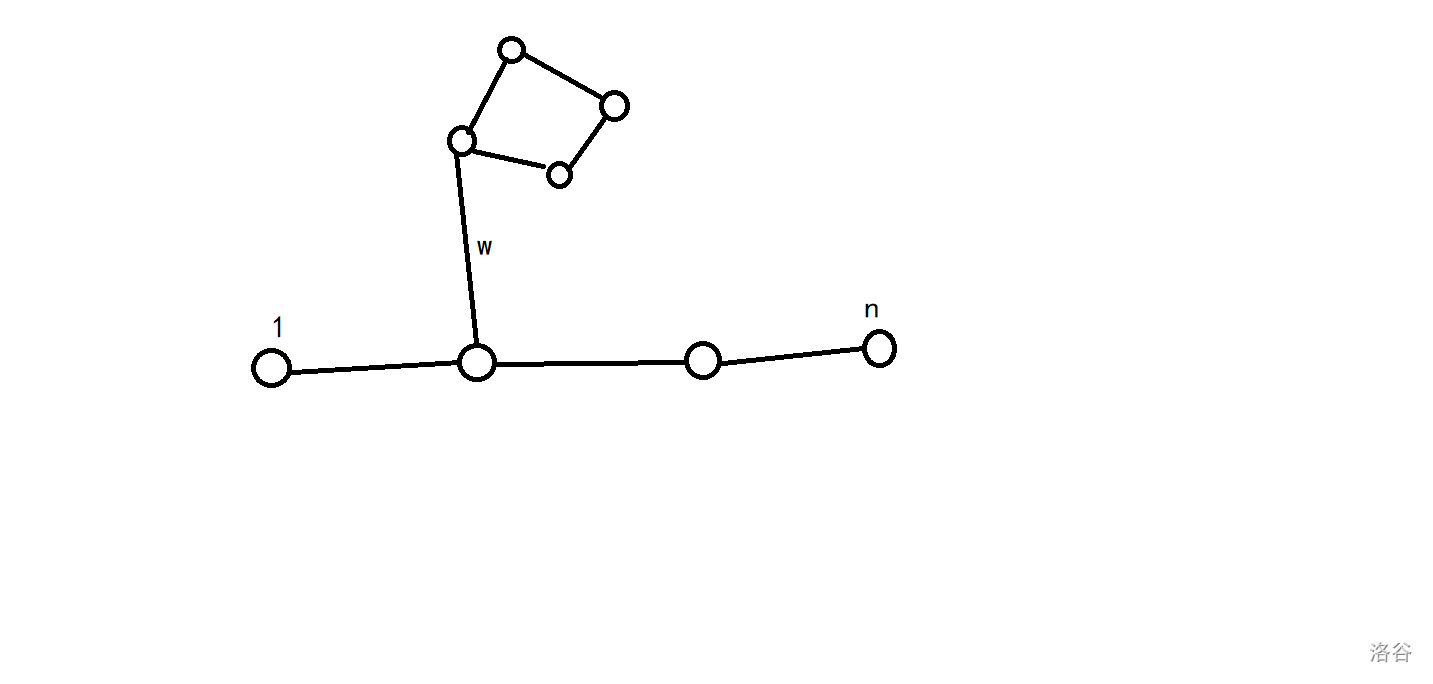
我们可以通过异或上这个环的权值而不异或上\(w\)，于是这启示我们答案必定是一条链带上好几个环。

现在考虑选哪条\(1\)到\(n\)链：

其实任意选一条即可，见下图：



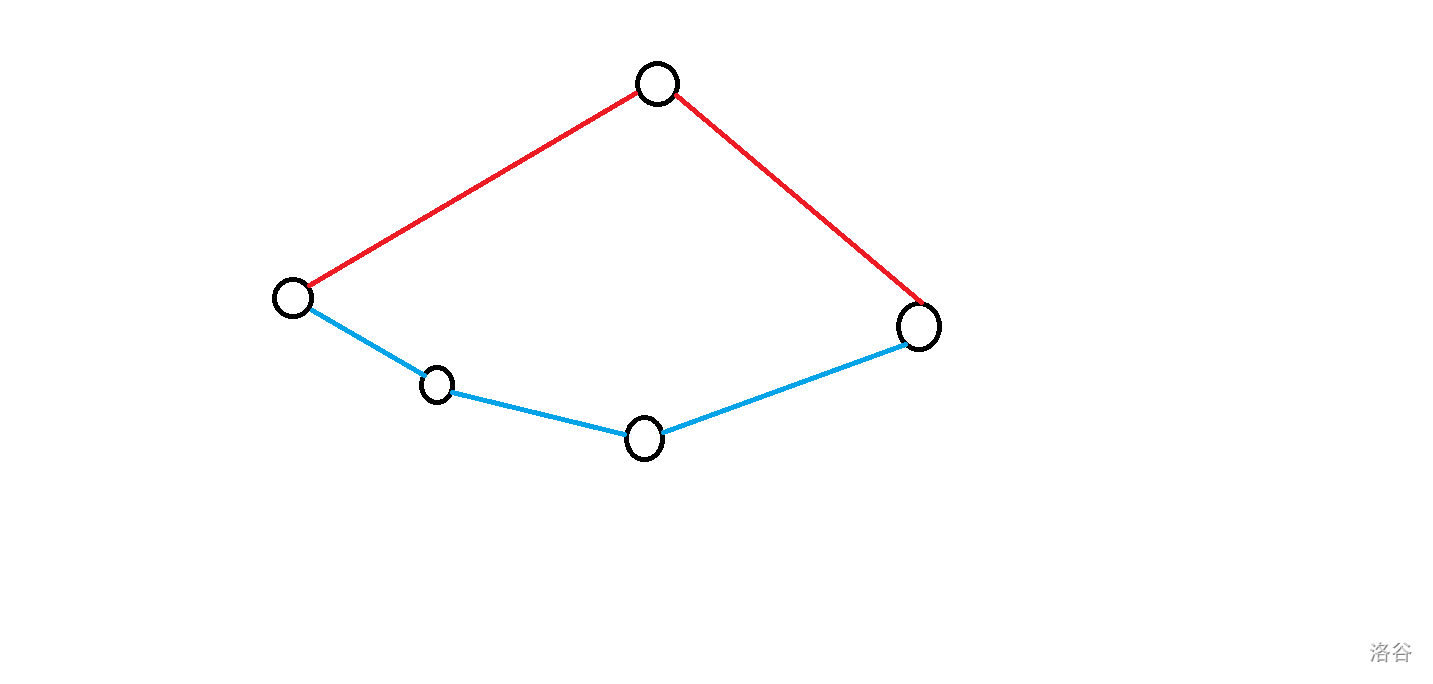
假设我们选了红的那条，而答案是选蓝色的那条，那么显然可以通过异或上这个环(都是\(1->n\)的路径，必然是环)使得当前值变为选蓝色那条。

dfs出一条链，将所有环插入线性基，求最大子集异或和。

code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=50010;
const int maxm=100010;
int n,m,cnt;
int head[maxn];
ll xord[65],sum[maxn];
bool vis[maxn];
struct edge{int to,nxt;ll dis;}e[maxm<<1];
inline ll read()
{
	char c=getchar();ll res=0,f=1;
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')res=res*10+c-'0',c=getchar();
	return res*f;
}
inline void add(int u,int v,ll w)
{
	e[++cnt].nxt=head[u];
	head[u]=cnt;
	e[cnt].to=v;
	e[cnt].dis=w;
}
inline void insert(ll x)
{
	for(int i=61;~i;i--)
	{
		if(!(x&(1ll<<i)))continue;
		if(!xord[i]){xord[i]=x;break;}
		else x^=xord[i];
	}
}
inline ll query(ll x)
{
	ll res=x;
	for(int i=61;~i;i--)if((res^xord[i])>res)res^=xord[i];
	return res;
}
void dfs(int x,ll res)
{
	vis[x]=1;sum[x]=res;
	for(int i=head[x];i;i=e[i].nxt)
	{
		int y=e[i].to;
		if(!vis[y])dfs(y,res^e[i].dis);
		else insert(res^sum[y]^e[i].dis);
	}
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();ll w=read();
		add(u,v,w),add(v,u,w);
	}
	dfs(1,0);
	printf("%lld",query(sum[n]));
	return 0;
}