3. 卷积神经网络(CNN)

关于数据集的介绍

top-N正确率指的是图像识别算法给出前N个答案中有一个是正确的概率。
在图像识别方面，基于卷积神经网络的图像识别算法给图像识别问题带来了质的飞跃，从2013年之后，基本上所有的研究都集中到了深度学习算法上。

卷积神经网络的结构

前面所介绍的神经网络的每两层之间的所有结点都是有边相连的，为了和卷积神经网络、循环神经网络区分，我们这种简单的神经网络结构为全连接神经网络。
对于卷积神经网络，相邻两层之间只有部分结点相连。卷积神经网络和全连接神经网络的唯一区别在于神经网络中相邻两层的连接方式。使用全连接神经网络处理图像的最大问题在于全连接层的参数太多。参数增多除了会导致计算速度减慢，还会导致过拟合的问题，所以需要一个更合理的神经网络结构来有效地减少神经网络中参数个数。卷神经网络就可以达到这个目的。

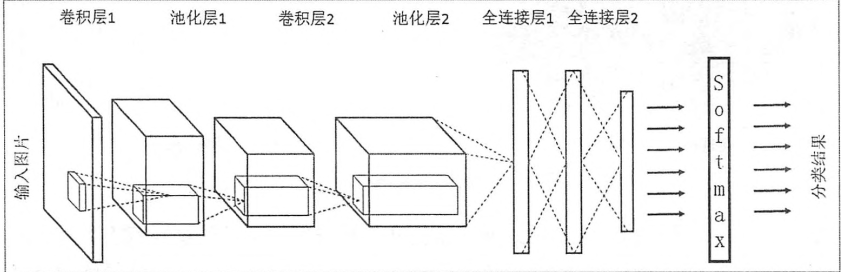
在卷积神经网络的额前几层中，每一层的结点都被组织成一个三维矩阵。例如处理Cifar数据集图片，可以将输入层组织层一个32323的矩阵。虚线部分展示了卷积神经网络的一个连接示意图，从中可以看出，卷积神经网络中前几层每一个结点只和上一层中部分的结点相连。

一个卷积神经网络主要由以下5个结构组成：

输入层。整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。从输入层开始，卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接。
卷积层。卷积层是一个卷积神经网络最为重要的部分。和传统全连接层不同，卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块通常有33或者55.卷积层试图将神经网络中的每一小块进行更加深入地分析从而得到抽象程度更高的特征。一般来说，通过卷积层处理过的节点矩阵会变的更深。
池化层。池化层神经网络不会改变三维矩阵的深度，但是它可以缩小矩阵的大小。池化操作可以认为是将一个分辨率高的图片转化为分辨率较低的图片。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而达到减少整个神经网络中参数的目的。
全连接层。在经过多轮卷积层和池化层的处理之后，在卷积神经网络的最后一般回事由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层的处理之后，可以认为图像中的信息已经被抽象成了信息含量更好的特征。我们可以将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成之后，任然需要使用全连接层来完成分类任务。
Softmax层。和全连接神经网络一样，Softmax层主要用于分类问题。通过Softmax层，可以得到当前样例属于不同种类的概率分布情况。

卷积层

过滤器的尺寸值得是一个过滤器输入节点矩阵的大小，而深度指的是输出单位节点矩阵的深度。
过滤器的前向传播过程就是通过左侧小矩阵中的节点计算出右侧单位矩阵中节点的过程。
在卷积神经网络中，每一个卷积层使用的过滤器参数都是一样的。这是卷积神经网络一个非常重要的性质。直观上理解，共享过滤器的参数可以使得图像上的内容不容易位置的影响。
共享每一个卷积层中过滤器参数可以巨幅减少神经网络上的参数。而且卷积层的参数个数和图片的大小无关，它只和过滤器的尺寸、深度以及当前层节点矩阵的深度有关，这使得卷积神经网络可以很好地扩展到更大的图像数据上。

池化层

卷积层之间往往会加上一个池化层。池化层可以非常有效地缩小矩阵的尺寸，从而减少最后全连接层中的参数。使用池化层既可以加快计算速度也有防止过拟合问题的作用。
和卷积层类似，池化层前向传播的过程也是通过移动一个类似过滤器的结构完成的。不过池化层过滤器中的计算不是节点的加权和，而是采用更加简单的最大值或者平均值运算。使用最大值操作的池化层被称之为最大池化层（max poolin）,这是被使用最多的池化层结构。使用平均值操作的池化层被称之为平均池化层（average pooling）。
池化层主要用于减小矩阵的长和宽。虽然池化层也可以减小矩阵的深度，但是实践中一般不这么干。
有研究指出池化层对模型效果的影响不大，但是目前主流的卷积神经网络模型中都含有池化层。