水仙花数计算

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬

1.题目描述

“3位水仙花数”是指一个三位整数，其各位数字的3次方和等于该数本身。例如：ABC是一个“3位水仙花数”，则：A的3次方＋B的3次方＋C的3次方 = ABC。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬

请按照从小到大的顺序输出所有的3位水仙花数，请用一个“逗号+空格”分隔输出结果。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬

2.程序代码：

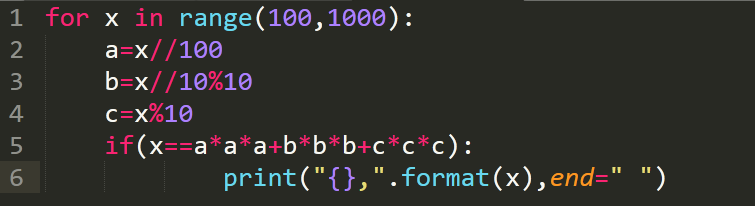
3.运行结果：

打印出三位数的水仙花数Python的更多相关文章

  1. 一个js函数算出任意位数的水仙花数

    一个算出任意位数的水仙花数的函数如下: var arr =[]; /*更改num确定取值范围*/ for(var num = 100; num <= 9999;num++){ /*多位数版本*/ ...

  2. python 求3到8位数的水仙花数Pycharm实现

    #-*- coding: utf-8-*-import timeimport math#获取3位数的水仙花数start1 = time.time()start = time.time() number ...

  3. 用Java编程计算出所有的＂水仙花数＂

    题目:打印出所有的 "水仙花数 ",所谓 "水仙花数 "是指一个三位数,其各位数字立方和等于该数本身.例如:153是一个 "水仙花数 ",因 ...

  4. 水仙花数-python

    题目: 求999以内的水仙花数? 分析: 如果一个3位数等于其各位数字的立方和,则称这个数为水仙花数. 例如:1^3 + 5^3+ 3^3 = 153,因此153就是一个水仙花数 我们需计算出153的 ...

  5. python3 练习题100例 （二十一）打印一定范围内的水仙花数

    题目内容: 水仙花数是指一个n位数 (n≥3),它的每个位上的数字的n次幂之和等于它本身. 例如:153是一个“水仙花数”,因为 153 是个 3位数,而1**3+5**3+3**3==153. 输入 ...

  6. 【C语言】（for循环嵌套）找出1000以内的水仙花数

    什么是水仙花数? 水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身(例如:1^3 + 5^3+ 3^3 = 153). 分析: 根据定义可知: a*a*a+b*b*b+c*c*c ...

  7. 【C语言】找出1000以内的水仙花数

    什么是水仙花数? 水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身(例如:1^3 + 5^3+ 3^3 = 153). 代码1: #include<stdio.h> ...

  8. 【C语言】创建一个函数，判断某一正整数是否为水仙花数，并调用这个函数找出1000以内所有水仙花数

    #include <stdio.h> int fun(int x) { int a, b, c; a = x / ; b = x % / ; c = x % ; if (x == a * ...

  9. python练习笔记——求三位的水仙花数

    百位数的立方 + 十位数的立方 +个位数的立方 = 原数 for m in range(1,10): for n in range(0,10): for i in range(0,10): a = m ...

随机推荐

  1. linux部署django项目流程（全）

    1.python3和python2共存配置 流程在下面网址中 https://www.cnblogs.com/vinic-xxm/p/11358894.html 2.安装依赖包 yum install ...

  2. 分布式异步框架celery

    Celery 1.什么是Clelery Celery是一个简单.灵活且可靠的,处理大量消息的分布式系统 专注于实时处理的异步任务队列 同时也支持任务调度 Celery架构 Celery的架构由三部分组 ...

  3. Prometheus（一）：Prometheus+Grafana 安装配置

    一.基础环境 系统 IP 监控主机 CentOS 7 192.168.56.200 被监控主机 CentOS 7 192.168.56.201 二.Prometheus服务端安装 以下操作皆在监控主机 ...

  4. Java期末复习——主观题

    JDK 和 JRE 有什么区别? JDK:Java Development Kit 的简称,java 开发工具包,提供了 java 的开发环境和运行环境. JRE:Java Runtime Envir ...

  5. Codeforces A. Playlist（暴力剪枝）

    题目描述: Playlist time limit per test 2 seconds memory limit per test 256 megabytes input standard inpu ...

  6. 注意力机制---Attention、local Attention、self Attention、Hierarchical attention

    一.编码-解码架构 目的:解决语音识别.机器翻译.知识问答等输出输入序列长度不相等的任务. C是输入的一个表达(representation),包含了输入序列的有效信息. 它可能是一个向量,也可能是一 ...

  7. nginx 请求限制

    1.nginx 请求限制 1.连接频率限制 - limit_conn_module 2.请求频率限制 - limit_req_module 连接限制的语法 请求限制的语法 limit_conn_zon ...

  8. PHP随机获取预设的值

    前面我们讲了php怎么获取随机数,<?php echo rand(1000,2000); ?> 一行代码就能搞定,如果要获取ASP,PHP,JAVASCRIPT,AJAX,CSS,JQUE ...

  9. keil中使用——变参数宏__VA_ARGS__

    本文说的__VA_ARGS__,就是一个可变参数宏,与printf中可变参数的宏定义一个道理,是新C99规范中增加的. __VA_ARGS__详情内容 1.关于__VA_ARGS__ __VA_ARG ...

  10. VIJOS-P1446 最短路上的统计

    JDOJ 1523: VIJOS-P1446 最短路上的统计 JDOJ传送门 Description 一个无向图上,没有自环,所有边的权值均为1,对于一个点对(a,b),我们要把所有a与b之间所有最短 ...