【贪心】【P5521】[yLOI2019] 梅深不见冬

B [yLOI2019] 梅深不见冬

Background

风，吹起梅岭的深冬；霜，如惊涛一样汹涌；雪，飘落后把所有烧成空，

像这场，捕捉不到的梦。

醒来时已是多年之久，宫门铜环才长了铁锈，

也开始生出离愁。

——银临《梅深不见冬》

Description

给定一棵 \(n\) 个节点的树，在树上行走，每次要么选择一个没有到达过的子节点，要么返回父节点。想要在一个节点 \(u\) 放上梅花当且仅当 \(u\) 的任意子节点 \(v\) 都被放上了 \(w_v\) 朵梅花。在任意时刻可以收回任意节点的梅花。对于每个节点，求如果想在这个节点放梅花，则至少需要准备多少梅花。

Limitations

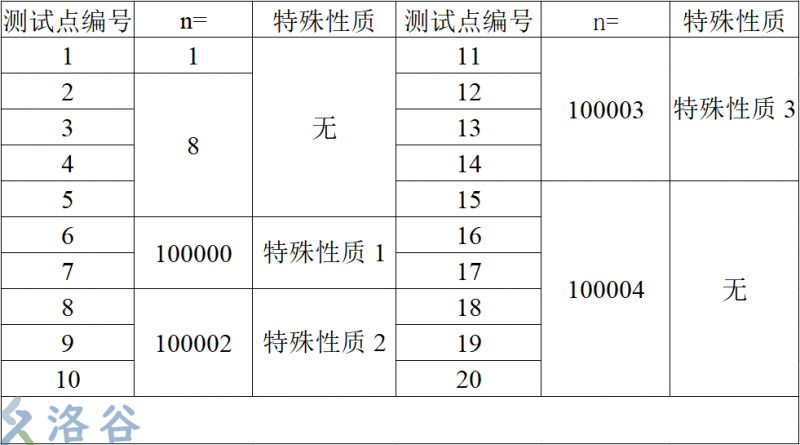
特殊性质1：每个节点的孩子结点个数不超过 \(2\)

特殊性质2：每个节点的孩子节点个数不超过 \(5\)

特殊性质3：任意一个节点到根的路径上的点数不超过 \(3\)，也即树高不超过 \(3\)

对于 \(100\%\) 的数据，保证 \(1 \leq w_i \leq 1000\)

Solution

测试点 \(1\)：

只有一个节点，输出 \(w_1\) 即可。期望得分 \(5~pts\)

测试点 \(2~\sim 5\)：

爆搜一个行走的顺序，然后可以 \(O(n)\) 判断是否合法。时间复杂度 \(O(n!\times n)\)，期望得分 \(20~pts\)

测试点 \(6~\sim~7\)：

注意到题目所规定的走法相当于按照树的某个dfs序走，即离开某个节点时必须遍历完它的子树，否则子树中一旦有一个节点没有被遍历到，则永远无法返回这个节点。

如果设在点 \(u\) 上放上 \(w_u\) 朵梅花最少需要 \(ans_u\) 朵梅花的话，考虑对于 \(u\) 的两个孩子 \(x,~y\)，如果先走 \(x\)，那么首先需要准备 \(ans_x\) 朵梅花，放上了 \(w_x\) 朵梅花，剩余了 \(ans_x - w_x\) 朵花，再走 \(y\)，需要准备 \(ans_y\) 朵花，当前有 \(ans_x - w_x\)，则需要额外准备 \(\max(ans_y - ans_x + w_x, 0)\) 朵花。先走 \(y\) 的情况类似，比较一下哪种情况更优即可。

时间复杂度 \(O(n)\)，期望得分 \(10~pts\)

测试点 \(8~\sim 10\)：

孩子节点个数不超过 \(5\)，于是爆搜一下走哪个孩子的顺序，用类似子任务 \(3\) 的方法统计，然后取最优的即可。

时间复杂度 \(O(n \times x!)\)，其中 \(x\) 为最大的节点孩子个数。期望得分 \(15~pts\)

测试点 \(11~\sim 14\)：

树高不超过 \(3\)，考虑第 \(3\) 层的节点，答案显然是他们自身的权值，第二层的节点，答案是第三层的权值和。

对于第一层的根节点 \(u\)，考虑放满他的孩子的花费和在这个节点上放梅花的花费的关系：

如果放满它的孩子花费为 \(c\)，它的孩子的权值和为 \(W\)，则会剩余 \(rest = c - W\) 朵梅花，由于 \(W\) 是个常量，\(rest\) 与 \(c\) 正相关。考虑当 \(w_u > rest\) 时，需要额外花费 \(w_u - rest\) 元，花费为 \(w_u - rest + rest = w_u\) 元，当 \(w_u \leq rest\) 时，花费 \(rest\) 元。由此可以发现，当 \(rest\) 减小时，所需要的花费不会增大。又因为 \(rest\) 与 \(c\) 正相关，因此放满它的孩子的花费变地，在这个节点上放梅花的花费不会增加。因此最小化放满它孩子的花费即可得到答案。

对于一个节点 \(x\)，设往这个节点上放上梅花至少需要准备 \(ans_x\) 朵梅花，而 \(x\) 的权值为 \(w_x\)，我们的问题是选择一个最优的放梅花的序列，使得最终需要准备的梅花最小。这个问题的答案是按照 \(ans_x - w_x\) 的不升序排序即可。

考虑证明这个结论：

设有两个节点 \(i,~j\)，设 \(a_i = ans_i - w_i,~a_j = ans_j - w_j\) 且 \(a_i > a_j\)。

考虑先放 \(i\) 再放 \(j\) 需要准备的梅花朵数是 \(\max(ans_i, ans_j + w_i)\)（一式），同理先放 \(j\) 所需要准备的梅花朵数是 \(\max(ans_j, ans_i + w_j)\)（二式）。

由于 \(a_i = ans_i - w_i\)，得 \(ans_i = a_i + w_i\)。\(ans_j\) 同理。对一式二式分别提出 \(w\)。

则

\[\text{一式} = \max(ans_i, ans_j + w_i) = \max(a_i + w_i, ans_j + w_i) = w_i + \max(a_i, ans_j)\]

\[\text{二式} = \max(ans_j,ans_i + w_j) = w_j + \max(a_j, ans_i) = w_j + \max(a_j, a_i + w_i) = w_j + a_i + w_i\]

考虑一式的 \(\max\) 如果取 \(a_i\)，那么 \(\text{一式} = w_i + a_i < w_i + a_i + w_j = \text{二式}\)

如果取 \(ans_j\)，那么 \(\text{一式} = w_i + w_j + a_j < w_i + w_j + w_i = \text{二式}\)

因此，一式恒小于二式，先放 \(i\) 更优。

据此做数学归纳可得，按照 \(ans - w\) 的不升序排序后的序列是最优的。

于是即可排序以后用上面的方式统计答案，时间复杂度 \(O(n \log n)\)，期望得分 \(20~pts\)

测试点 \(15~\sim 20\)：

发现上面的结论可以应用于这棵树上的任何一个节点，于是每个节点都按照这样的方法排序即可。时间复杂度 \(O(n \log n)\)，期望得分 \(30 pts\)。