【洛谷P5019】铺设道路

题目链接

众所周知，这道题和积木大赛是同一道题

题意就是给出一段自然数序列，每次操作\((L,R)\)把区间\([L,R]\)的数全部减一，不允许出现负数，问把序列变为零的最小操作次数

贪心做法

样例

6
4 3 2 5 3 5

大概长这个样子

我们考虑第一列的四块格子，最少需要\(4\)次操作给消除掉

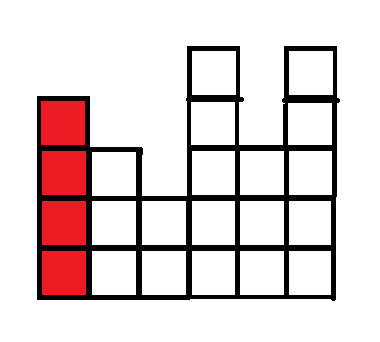
在考虑第二列的\(3\)个格子时，发现都可以在第一列的\(4\)次操作中一起消除掉

第三列的格子也都可以一起消除掉

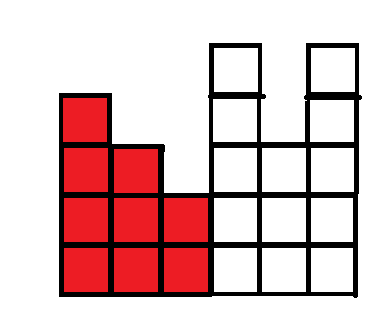
考虑第四列，我们可以发现，第四列下面的两个格子在前面的操作中可以一起消除，但是上面的三个是至少再进行三次操作才能消除的

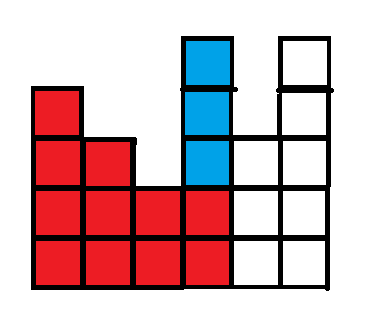
而第五列下面的两个格子在第一列的操作中可以消除，上面的一个格子可以在第四列的操作中删除

考虑第六列，上面的\(2\)个格子是前面操作消除不了的，需要\(2\)次操作

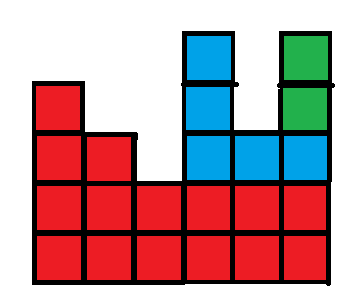
那么答案就是\(4+3+2=9\)

这样大概可以总结出做法：当\(a_{i-1}<a_i\)时，\(ans+= a_i - a_{i-1}\)

贪心证明

下面用差分序列给出这个贪心的证明：

我们对原序列\(\{a_i\}\)维护一个差分数组\(\{diff_i\}\)

原序列不妨在最后加一个\(0\)，

6
4 3 2 5 3 5 0

差分数组是

4 -1 -1 3 -2 2 -5

每次操作可以表示为\(diff[L]--\),\(diff[R+1]++\)

最终的状态就是差分数组全部变成\(0\)

首先，每次操作最多让一个大于零的\(diff_i\) \(-1\)，所以 最优解\(ans>=sum(diff_i,diff_i>0)\)

下面要证明 \(ans=sum(diff_i,diff_i>0)\)

\(a_{n+1}=0\) => \(sum(diff_i)=0\) => \(sum(diff_i,diff_i>0)+sum(diff_i,diff_i<0)=0\)

我们只要每次操作能让一个大于\(0\)的\(diff_i\) \(-1\),同时后面一个小于\(0\)的\(diff_i\) \(+1\)才能够使\(ans=sum(diff_i,diff_i>0)\)

然而有一个限制条件：\(a_L\)~\(a_R\)之间没有零 否则这个操作就是不合法的

我们可以利用以下性质构造解法：

性质1：由题意知任意时刻\(a_i>=0\)，若\(diff_i>0\) 则\(a_i>a_{i-1}>=0\),得\(a_i>0\)

性质2：由于\(a_{n+1}=sum(diff_i)=0\),对于一个大于零的\(diff_i\),\(sum(diff_{1}\)~\(diff_{i})=a_i>0\),它的后面一定存在小于零的\(diff_i\)

于是有：每次选一个大于零的\(diff_i\)作为操作的左端点\(L\),它右边的第一个小于零的\(diff_j\)作为\(R+1\)，已知\(a_L>0\),\([L,R]\)中任意\(diff_k>=0\),可得任意\(a_k\)属于\([L,R]\),\(a_k>=a_{k-1}>=a_L>0\),因此该操作合法

所以存在至少一种操作方法可以在\(sum(diff_i,diff_i>0)\)次操作后使得\(diff\)序列全部为\(0\)，\(ans=sum(diff_i,diff_i>0)\)