[SOJ #686]抢救(2019-11-7考试)/[洛谷P3625][APIO2009]采油区域

题目大意

有一个\(n\times m\)的网格，\((x,y)\)权值为\(a_{x,y}\)，要求从中选取三个不相交的\(k\times k\)的正方形使得它们权值最大。\(n,m,k\leqslant1500\)

题解

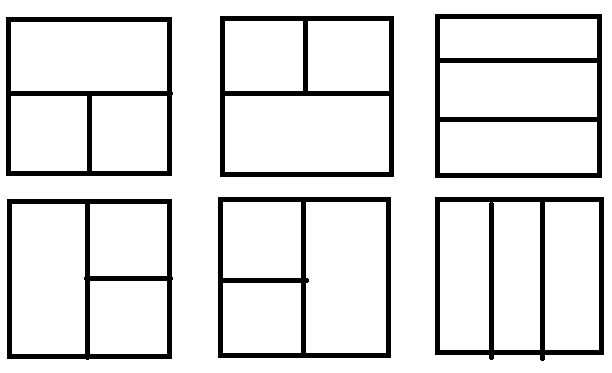
其实，只有如下六种方法分割网格：

对于每一种情况，我们在每个小方格中找最大的\(k\times k\)的正方形相加即可。可以令\(a[i][j],b[i][j],c[i][j],d[i][j]\)分别表示\((i,j)\)的左上、右上、左下、右下的区域中最大的\(k\times k\)的正方形的权值，然后就可以计算了

卡点

无

C++ Code：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cctype>
const int maxn = 1510;
namespace io {
	struct istream {
#define M (1 << 24)
		char buf[M], *ch = buf - 1;
		inline istream() { fread(buf, 1, M, stdin); }
		inline istream& operator >> (int &x) {
			while (isspace(*++ch));
			for (x = *ch & 15; isdigit(*++ch); ) x = x * 10 + (*ch & 15);
			return *this;
		}
#undef M
	} cin;
}

int n, m, k, ans, s[maxn][maxn];
int a[maxn][maxn], b[maxn][maxn], c[maxn][maxn], d[maxn][maxn];
/*
 * a | b
 * - - -
 * c | d
 */
int main() {
	std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
	io::cin >> n >> m >> k;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			io::cin >> s[i][j];
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			s[i][j] += s[i][j - 1];
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			s[i][j] += s[i - 1][j];
	for (int i = n; i >= k; --i)
		for (int j = m; j >= k; --j)
			s[i][j] += s[i - k][j - k] - s[i - k][j] - s[i][j - k];
	for (int i = k; i <= n; ++i)
		for (int j = k; j <= m; ++j)
			a[i][j] = std::max({ s[i][j], a[i - 1][j], a[i][j - 1] });
	for (int i = k; i <= n; ++i)
		for (int j = m - k + 1; j; --j)
			b[i][j] = std::max({ s[i][j + k - 1], b[i - 1][j], b[i][j + 1] });
	for (int i = n - k + 1; i; --i)
		for (int j = k; j <= m; ++j)
			c[i][j] = std::max({ s[i + k - 1][j], c[i + 1][j], c[i][j - 1] });
	for (int i = n - k + 1; i; --i)
		for (int j = m - k + 1; j; --j)
			d[i][j] = std::max({ s[i + k - 1][j + k - 1], d[i + 1][j], d[i][j + 1] });
	for (int i = k; i <= n - k; ++i)
		for (int j = k; j <= m - k; ++j)
			ans = std::max(ans, a[i][j] + b[i][j + 1] + c[i + 1][m]);
	for (int i = k; i <= n - k; ++i)
		for (int j = k; j <= m - k; ++j)
			ans = std::max(ans, a[i][m] + c[i + 1][j] + d[i + 1][j + 1]);
	for (int i = k; i <= n - k; ++i)
		for (int j = k; j <= m - k; ++j)
			ans = std::max(ans, a[i][j] + c[i + 1][j] + b[n][j + 1]);
	for (int i = k; i <= n - k; ++i)
		for (int j = k; j <= m - k; ++j)
			ans = std::max(ans, a[n][j] + b[i][j + 1] + d[i + 1][j + 1]);
	for (int i = k; i <= n; ++i)
		for (int j = 2 * k; j <= m - k; ++j)
			ans = std::max(ans, s[i][j] + a[n][j - k] + b[n][j + 1]);
	for (int i = 2 * k; i <= n - k; ++i)
		for (int j = k; j <= m; ++j)
			ans = std::max(ans, s[i][j] + a[i - k][m] + c[i + 1][m]);
	std::cout << ans << '\n';
	return 0;
}