洛谷10月月赛R2·浴谷八连测R3题解

　　早上打一半就回家了...

　　T1傻逼题不说了...而且我的写法比题解要傻逼很多T T

　　T2可以发现，我们强制最大值所在的块是以左上为边界的倒三角，然后旋转4次就可以遍历所有的情况。所以二分极差，把最大值所能扩展到的（mp[i][j]+mid>=mx）最大倒三角求出来，剩下的数减去最小值判断一下是否小于等于极差，如果是的话答案可行。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=,inf=1e9;
int mn,mx;
int n[],m[],mp[][maxn][maxn];
bool v[maxn][maxn];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
void rotate(int x,int y)
{
    for(int i=;i<=n[x];i++)
    for(int j=;j<=m[x];j++)
    mp[y][j][n[x]-i+]=mp[x][i][j];
    n[y]=m[x];m[y]=n[x];
}
bool check(int x,int mid)
{
    memset(v,,sizeof(v));
    int now=m[x];
    for(int i=;i<=n[x];i++)
    for(int j=;j<=now;j++)
    if(mp[x][i][j]+mid<mx){now=j-;break;}
    else v[i][j]=;
    for(int i=n[x];i;i--)
    for(int j=m[x];j;j--)
    if(v[i][j])break;
    else if(mp[x][i][j]-mid>mn)return ;
    return ;
}
int main()
{
    read(n[]);read(m[]);mn=inf;
    for(int i=;i<=n[];i++)for(int j=;j<=m[];j++)read(mp[][i][j]),mx=max(mx,mp[][i][j]),mn=min(mn,mp[][i][j]);
    rotate(,);rotate(,);rotate(,);
    int l=,r=mx-mn;
    while(l<r)
    {
        int mid=(l+r)>>;
        if(check(,mid)||check(,mid)||check(,mid)||check(,mid))r=mid;
        else l=mid+;
    }
    printf("%d\n",l);
    return ;
}

　　T3超喵的题啊，虽然标程好像出了点小偏差，已经跟管理员反馈了，但是现在暂时还没有更正，还是先水一篇博客要紧...

　　首先要知道扩展欧拉定理...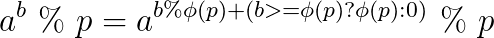

　　我们知道p<=2e7，所以可以先预处理出2e7内的phi（我写个埃式筛怎么比线性筛慢那么多T T）。因为一个数最多经过log次求phi的操作就会变成1，当变成1的时候后面的数就没有意义了，所以对于一个区间的询问，我们可以递归地计算指数，直到1就返回1，或者直到区间扫完就返回当前位置的值，效率O(logP)。但是我们怎么判断当前指数是否大于phi（p）呢，可以发现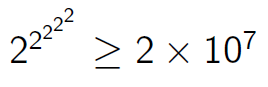，所以我们只要知道后5位的数就可以判断指数是否大于phi（p）了。然后一边递归一边快速幂，用BIT维护区间修改，单点查询，就可以了。

　　这个代码现在只有90分，等管理员更正数据后就能AC了...

　　UPD:数据已更正，状态里瞬间只剩下我一个人AC...

　　UPD:改成线性筛快了好多...

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=,inf=1e9,lim=2e7;
int n,m,ty,x,y,z,cnt;
int phi[],v[maxn],prime[];
ll tree[maxn],a[maxn];
bool vis[];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
inline int lowbit(int x){return x&-x;}
inline void add(int x,int delta){for(;x<=n;x+=lowbit(x))tree[x]+=delta;};
inline ll querysum(int x){ll sum=;for(;x;x-=lowbit(x))sum+=tree[x];return sum;}
inline ll query(int x)
{
    if(v[x]==m+)return a[x];
    v[x]=m+;return a[x]=querysum(x);
}
inline int power(int a,int b,int mod)
{
    if(!a)return ;int ans=;
    for(;b;b>>=,a=1ll*a*a%mod)
    if(b&)ans=1ll*ans*a%mod;
    return ans;
}
int solve(int l,int r,int mod)
{
    if(mod==)return ;
    ll now=query(l)%mod;if(!now)return ;if(l==r)return now;
    int nxt=min(l+,r);
    for(int i=l+;i<nxt;i++)if(query(i)==){nxt=r=i;break;}
    ll last=query(nxt),x;
    if(last>=phi[mod])return power(now,solve(l+,r,phi[mod])+phi[mod],mod);
    for(int i=nxt-;i>l;i--)
    {
        ll mi=last;last=;x=query(i);
        for(int j=;j<=mi;j++)
        {
            last*=x;
            if(last>=phi[mod])return power(now,solve(l+,r,phi[mod])+phi[mod],mod);
        }
    }
    return power(now,solve(l+,r,phi[mod]),mod);
}
inline void getphi()
{
    phi[]=;
    for(int i=;i<=lim;i++)
    {
        if(!vis[i])prime[++cnt]=i,phi[i]=i-;
        for(int j=;j<=cnt;j++)
        {
            int t=i*prime[j];if(t>lim)break;
            vis[t]=;
            if(i%prime[j]==){phi[t]=phi[i]*prime[j];break;}
            phi[t]=phi[i]*(prime[j]-);
        }
    }
}
int main()
{
    getphi();read(n);read(m);int pre=;
    for(int i=;i<=n;i++)read(x),add(i,x-pre),pre=x;
    while(m--)
    {
        read(ty);read(x);read(y);read(z);
        if(ty==)add(x,z),add(y+,-z);
        else printf("%d\n",solve(x,y,z)%z);
    }
    return ;
}