【25.64%】【codeforces 570E】Pig and Palindromes

time limit per test4 seconds

memory limit per test256 megabytes

inputstandard input

outputstandard output

Peppa the Pig was walking and walked into the forest. What a strange coincidence! The forest has the shape of a rectangle, consisting of n rows and m columns. We enumerate the rows of the rectangle from top to bottom with numbers from 1 to n, and the columns — from left to right with numbers from 1 to m. Let’s denote the cell at the intersection of the r-th row and the c-th column as (r, c).

Initially the pig stands in cell (1, 1), and in the end she wants to be in cell (n, m). Since the pig is in a hurry to get home, she can go from cell (r, c), only to either cell (r + 1, c) or (r, c + 1). She cannot leave the forest.

The forest, where the pig is, is very unusual. Some cells of the forest similar to each other, and some look very different. Peppa enjoys taking pictures and at every step she takes a picture of the cell where she is now. The path through the forest is considered to be beautiful if photographs taken on her way, can be viewed in both forward and in reverse order, showing the same sequence of photos. More formally, the line formed by the cells in order of visiting should be a palindrome (you can read a formal definition of a palindrome in the previous problem).

Count the number of beautiful paths from cell (1, 1) to cell (n, m). Since this number can be very large, determine the remainder after dividing it by 109 + 7.

Input

The first line contains two integers n, m (1 ≤ n, m ≤ 500) — the height and width of the field.

Each of the following n lines contains m lowercase English letters identifying the types of cells of the forest. Identical cells are represented by identical letters, different cells are represented by different letters.

Output

Print a single integer — the number of beautiful paths modulo 109 + 7.

Examples

input

3 4

aaab

baaa

abba

output

3

Note

Picture illustrating possibilities for the sample test.

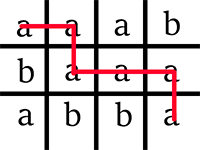
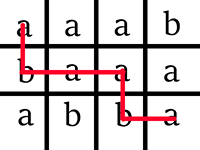
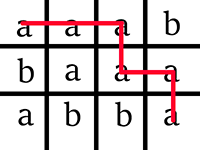
【题目链接】:http://codeforces.com/contest/570/problem/E

【题解】



可以看成是两个人在走路;

一个人(x1,y1)从左上角往右下角走;

另外一个人(x2,y2)从右下角往左上角走;

则设f[step][x1][y1][x2][y2]表示两个人都走了step步,第一个人到了x1,y1第二个人到了x2,y2的方案数;

(要时刻满足x1<=x2且y1<=y2);

则f[step][x1][y1][x2][y2]=f[step-1][x1-1][y1][x2+1][y2]…..

但是这样搞空间复杂度太大;

注意到，如果step确定了,则根据x1,x2我们完全可以直接得到y1和y2;

因为

y1+x1-1=step

n-x2+m-y2+1=step;

则我们可以减小f数组的维数

变成

f[step][x1][x2];

(这样枚举step最后要变成(n+m)/2,它们最后才会相遇或相邻);

(要时刻满足x1<=x2且y1<=y2);

而f[step]只与f[step-1]有关;

所以考虑用滚动数组;

转移方程也变成

f[now][x1][x2] = f[now^1][x1][x2]+f[now^1][x1-1][x2]+f[now^1][x1-1][x2+1]+f[now^1][x1][x2+1];

最后在f[1..n][i][i]中找最大值;

但如果n+m为奇数；

则它们最后到的不是同一格

可能是相邻的上下两个或左右两格;(只有n+m为偶数才会到同一格);





【完整代码】

#include <bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define rei(x) scanf("%d",&x)
#define rel(x) scanf("%I64d",&x)

typedef pair<int,int> pii;
typedef pair<LL,LL> pll;

const int MAXN = 550;
const int MOD = 1e9+7;
const int dx[9] = {0,1,-1,0,0,-1,-1,1,1};
const int dy[9] = {0,0,0,-1,1,-1,1,-1,1};
const double pi = acos(-1.0);

int n,m,now = 0;
char s[MAXN][MAXN];
int f[2][MAXN][MAXN];

void add(int &a,int &b)
{
    a = a+b;
    if (a>=MOD) a -= MOD;
}

int main()
{
    //freopen("F:\\rush.txt","r",stdin);
    rei(n);rei(m);
    rep1(i,1,n)
        scanf("%s",s[i]+1);
    if (s[1][1]!=s[n][m])
    {
        puts("0");
        return 0;
    }
    f[now][1][n] = 1;
    rep1(step,2,(n+m)/2)
    {
        now^=1;
        memset(f[now],0,sizeof f[now]);
        rep1(x1,1,step)
            rep2(x2,n,n-step+1)
            {
                int y1 = step+1-x1,y2 = n-x2+1+m-step;
                if (y1>y2 || x1>x2)
                    continue;
                if (s[x1][y1]==s[x2][y2])
                {
                    add(f[now][x1][x2],f[now^1][x1][x2]);
                    add(f[now][x1][x2],f[now^1][x1-1][x2]);
                    add(f[now][x1][x2],f[now^1][x1-1][x2+1]);
                    add(f[now][x1][x2],f[now^1][x1][x2+1]);
                }
            }
    }
    int ans = 0;
    if ((n+m)&1)
    {
        rep1(i,1,n)
                add(ans,f[now][i][i]),add(ans,f[now][i][i+1]);
    }
    else
        rep1(i,1,n)
            add(ans,f[now][i][i]);
    printf("%d\n",ans);
    return 0;
}