calc BZOJ 2655

calc

【问题描述】

一个序列a1,...,an是合法的，当且仅当：

长度为给定的n。

a1,...,an都是[1,A]中的整数。

a1,...,an互不相等。

一个序列的值定义为它里面所有数的乘积，即a1a2...an。

求所有不同合法序列的值的和。

两个序列不同当且仅当他们任意一位不一样。

输出答案对一个数mod取余的结果。

【输入格式】

一行3个数，A，n，mod。意义为上面所说的。

【输出格式】

一行结果。

【样例输入】

9 7 10007

【样例输出】

3611

HINT

【数据规模】

0:A<=10,n<=10。

1..3:A<=1000,n<=20。

4..9:A<=10^9,n<=20。

10..19:A<=10^9,n<=500。。

全部:mod<=10^9,并且mod为素数，mod>A>n+1。

---

题解：

设 f[i][j] 为用不大于A的数组成的有序合法序列方案数

转移方程：（是否选取 i 这个数字）

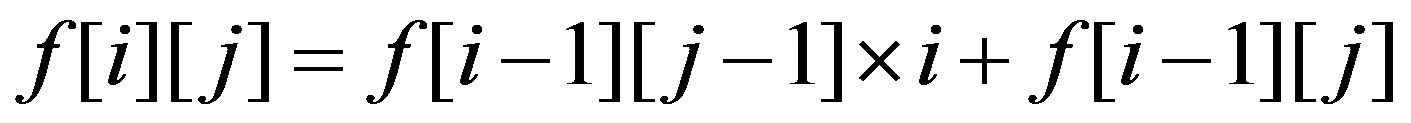
题目要求无序，那么最后乘上 n! 即可

细心观察一小下，发现它是一个有 2n 项的多项式

用拉格朗日插值法：

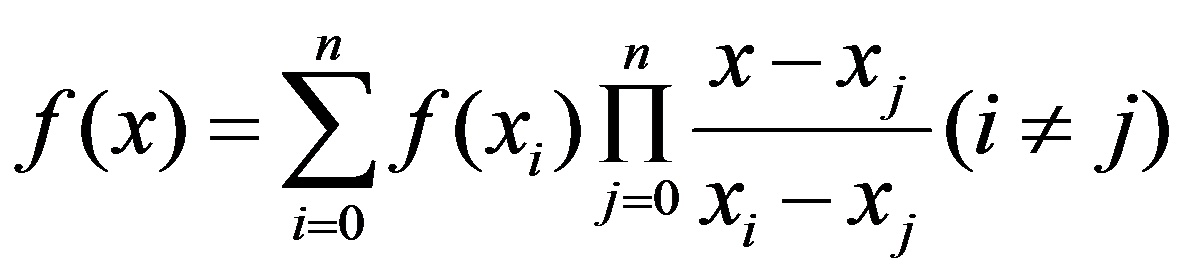
 #include<cmath>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 typedef long long lo;
 inline int Get()
 {
     int x;
     char c;
     bool o = false;
     while((c = getchar()) < '' || c > '')
         if(c == '-') o = true;
     x = c - '';
     while((c = getchar()) >= '' && c <= '')
         x = x *  + c - '';
     return (o) ? -x : x;
 }
 const int maxn = ;
 int f[maxn][maxn];
 int fac[maxn];
 int x[maxn], y[maxn];
 int a, n, m, mo;
 int z, v, ans;
 int num;
 inline void Dp()
 {
     f[][] = ;
     for(int i = ; i <= m; ++i)
         for(int j = ; j <= n; ++j)
         {
             f[i][j] = f[i - ][j];
             if(j) f[i][j] += (lo) f[i - ][j - ] * i % mo;
             if(f[i][j] >= mo) f[i][j] -= mo;
         }
 }
 inline void Fac()
 {
     fac[] = ;
     for(int i = ; i <= n; ++i) fac[i] = (lo) fac[i - ] * i % mo;
 }
 inline void Sun()
 {
     num = ;
     for(int i = ; i <= m; ++i)
         if(f[i][n])
         {
             x[++num] = i, y[num] = f[i][n];
             if(num == (n <<  | )) return;
         }
 }
 inline int Mod(int x)
 {
     if(x < ) x += mo;
     return x;
 }
 inline int Pow(int x, int n)
 {
     int sum = ;
     while(n)
     {
         if(n & ) sum = (lo) sum * x % mo;
         x = (lo) x * x % mo;
         n >>= ;
     }
     return sum;
 }
 int main()
 {
     a = Get(), n = Get(), mo = Get();
     m = n << ;
     Dp();
     Fac();
     if(m >= a)
     {
         printf("%d", (lo) f[a][n] * fac[n] % mo);
         return ;
     }
     Sun();
     z = ;
     for(int i = ; i <= num; ++i) z = (lo) z * Mod(a - x[i]) % mo;
     for(int i = ; i <= num; ++i)
     {
         v = Mod(a - x[i]);
         for(int j = ; j <= num; ++j)
             if(i != j)
                 v = (lo) v * Mod(x[i] - x[j]) % mo;
         ans = ans + (lo) y[i] * z % mo * Pow(v, mo - ) % mo;
         if(ans >= mo) ans -= mo;
     }
     printf("%d", (lo) ans * fac[n] % mo);
 }