BZOJ4446 [Scoi2015]小凸玩密室 【树形Dp】

题目

小凸和小方相约玩密室逃脱，这个密室是一棵有n个节点的完全二叉树，每个节点有一个灯泡。点亮所有灯

泡即可逃出密室。每个灯泡有个权值Ai，每条边也有个权值bi。点亮第1个灯泡不需要花费，之后每点亮4

个新的灯泡V的花费，等于上一个被点亮的灯泡U到这个点V的距离Du,v，乘以这个点的权值Av。在点灯

的过程中，要保证任意时刻所有被点亮的灯泡必须连通，在点亮一个灯泡后必须先点亮其子树所有灯泡才能点亮其他灯泡。请告诉他们，逃出密室的最少花费是多少。

输入格式

第1行包含1个数n，代表节点的个数

第2行包含n个数，代表每个节点的权值ai。(i=l，2，…，n)

第3行包含n-l个数，代表每条边的权值bi，第i号边是由第(i+1)/2号点连向第i+l号点的边。

(i=l，2...N-1)

输出格式

输出包含1个数，代表最少的花费。

输入样例

3

5 1 2

2 1

输出样例

5

提示

对于100%的数据，1≤N≤2×105，1<Ai,Bi≤10^5

题解

首先，此题有一些比较重要的性质：

①这棵树是一棵完全二叉树

②每次要处理完一个子树才能往祖先节点处理

③所有时刻点亮的点必须联通

④初始可以从任意点开始点亮

由这些性质，我们会发现从一个节点出发，整棵树被点亮的顺序是比较固定的，

点亮一个点u，然后点亮其子树

然后再点亮u的父亲，然后点亮u的兄弟的子树

然后点亮u父亲的父亲，点亮u父亲的父亲的兄弟的子树

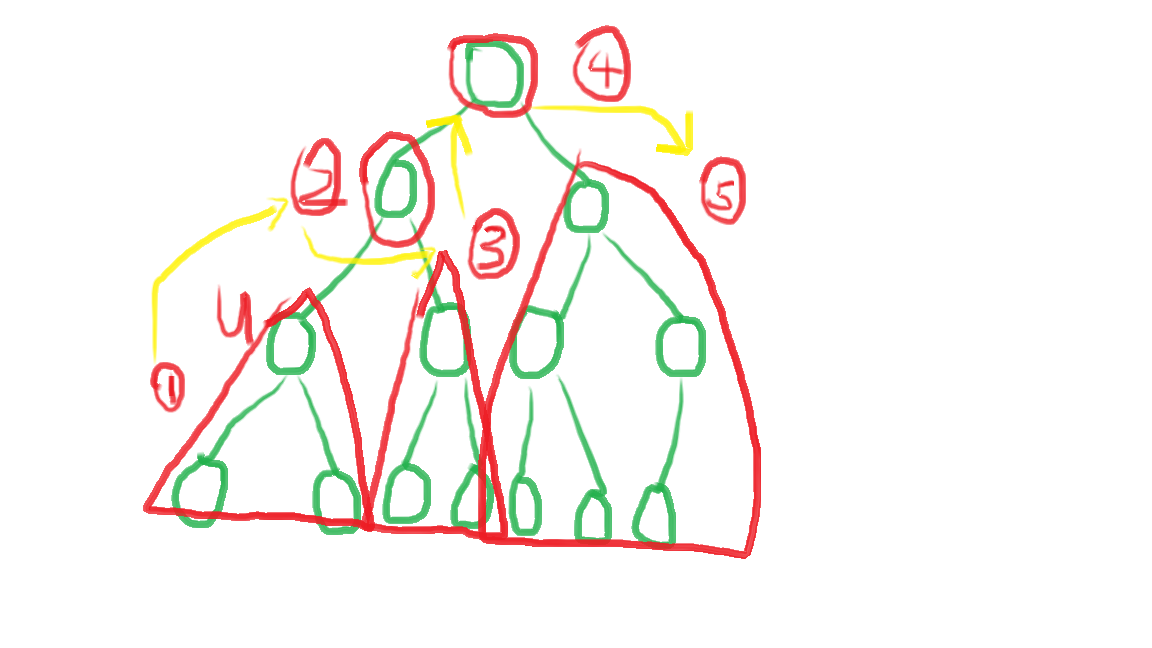
像这样

设\(g[i][j]\)表示从\(i\)节点开始，点亮\(i\)所在子树，然后点亮\(i\)位于第\(j\)层的祖先的最小费用

如果我们知道\(g[i][j]\)，就可以枚举出发点，然后模拟上图的过程算出最后的代价

现在问题转化为如何求\(g[i][j]\)

考虑树形dp的模式

对于节点u，我们想要求出\(g[u][j]\)

①u为叶子节点，直接计算到\(j\)层祖先的价值，如果该祖先为v,则\(g[u][j] = (d[u] - d[v])*a[v]\)【d[u]指到根距离】

②u只有一个儿子，记为s，当然是\(g[u][j] = b[s] * a[s] + g[s][j]\)

③u有两个儿子

此时有两种选择:

1°先走左子树，然后走到右子树，再走到\(j\)层的父亲

2°先走右子树，然后走到左子树，再走到\(j\)层的父亲

对于两种选择，我们求出最小者

诶？等等，走到父亲的花费就是\(g\)，但走到兄弟的花费呢？

我们记\(f[i][j]\)表示从节点\(i\)访问其子树并走到第\(j\)层的兄弟的最小花费

那么这两种选择就可以写成：

\(min(b[ls] * a[ls] + f[ls][dep[rs]] + g[rs][j],
b[rs] * a[rs] + f[rs][dep[ls]] + g[ls][j])\)

现在问题就转化成了求\(f[i][j]\)

用同样的思想，我们对节点u有：

①如果u为叶子节点，可以直接求出其\(f[i][j] = dis * a[v]\)

②如果u只有一个儿子，记为s，\(f[i][j] = b[s] * a[s] + f[s][j]\)

③u有两个儿子，

同样有两种类似的选择

\(min(b[ls] * a[ls] + f[ls][dep[rs]] + f[rs][j],
b[rs] * a[rs] + f[rs][dep[ls]] + f[ls][j])\)

那么这样，这题我们就做完啦

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u]; k; k = ed[k].nxt)
using namespace std;
const int maxn = 200005,maxm = 100005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57) {out = (out << 1) + (out << 3) + c - '0'; c = getchar();}
	return out * flag;
}
LL g[maxn][20],f[maxn][20];
LL n,a[maxn],b[maxn],d[maxn],dep[maxn];
void cal(){
	for (int i = n; i; i--){
		int ls = i << 1,rs = i << 1 | 1;
		for (int j = dep[i]; j; j--){
			int  s = (i >> (dep[i] - j)) ^ 1,fa = s >> 1;
			if (ls > n) f[i][j] = (d[i] - d[fa] + b[s]) * a[s];
			else if (rs > n) f[i][j] = a[ls] * b[ls] + f[ls][j];
			else f[i][j] = min(
					a[ls] * b[ls] + f[ls][dep[ls]] + f[rs][j],
					a[rs] * b[rs] + f[rs][dep[rs]] + f[ls][j]
				);
		}
	}
	for (int i = n; i; i--){
		int ls = i << 1,rs = i << 1 | 1;
		if (ls > n) g[i][0] = 0;
		else if (rs > n) g[i][0] = a[ls] * b[ls] + g[ls][0];
		else g[i][0] = min(
				a[ls] * b[ls] + f[ls][dep[ls]] + g[rs][0],
				a[rs] * b[rs] + f[rs][dep[rs]] + g[ls][0]
			);
		for (int j = dep[i] - 1; j; j--){
			int fa = (i >> (dep[i] - j));
			if (ls > n) g[i][j] = (d[i] - d[fa]) * a[fa];
			else if (rs > n) g[i][j] = a[ls] * b[ls] + g[ls][j];
			else g[i][j] = min(
					a[ls] * b[ls] + f[ls][dep[ls]] + g[rs][j],
					a[rs] * b[rs] + f[rs][dep[rs]] + g[ls][j]
				);
		}
	}
}
void solve(){
	LL ans = g[1][0];
	for (int i = 2; i <= n; i++){
		LL cost = g[i][dep[i] - 1];
		int x,fa;
		for (int u = i; u > 1; u >>= 1){
			x = u ^ 1; fa = u >> 1;
			if (x > n) cost += b[fa] * a[fa >> 1];
			else cost += a[x] * b[x] + g[x][dep[fa] - 1];
		}
		ans = min(ans,cost);
	}
	printf("%lld\n",ans);
}
int main(){
	n = read();
	for (int i = 1; i <= n; i++) a[i] = read();
	for (int i = 2; i <= n; i++) b[i] = read();
	dep[1] = 1;
	for (int i = 1; i <= n; i++){
		if ((i << 1) <= n){
			dep[i << 1] = dep[i] + 1;
			d[i << 1] = d[i] + b[i << 1];
		}
		if ((i << 1 | 1) <= n){
			dep[i << 1 | 1] = dep[i] + 1;
			d[i << 1 | 1] = d[i] + b[i << 1 | 1];
		}
	}
	cal();
	solve();
	return 0;
}