希尔排序(Shellsort)

首先，Shell是发明这个算法的人名，不是这个算法的思想或者特点。

希尔排序，也称为增量递减排序。基本思路，是把原来的序列，等效视为一个矩阵的形式。矩阵的列数，也称为宽度或者增量，记为w。

假设数组A[n]以及矩阵B[][]，对于两者的对应关系，可以记为A[k]=B[k/w][k%w]。也就是说，A中的元素会按照先行后列的顺序排列，即先左后右、先上后下的顺序放入矩阵B中。

对于增量或者说矩阵的宽度w，会有许多策略进行选择。假设w={1,2,4,8,16,32...}。从w的集合中选择小于数组元素数量n的最大元素w[i]，并且选取w[0]到w[i]之间的所有增量，从w[i]开始，按照矩阵B中的每一列进行排序。这里的排序必须是输入敏感的，通常采用插入排序。本次完成后，取下一个w，再按照每列进行排序。直到w=1，矩阵退化为向量，排序完成。

 int max(int* H, int n, int size)
 {
     int i = ;
     while (i < n&&size > H[i]) i++;
     return i - ;
 }
 void shellSort(int* A, int lo, int hi)//[lo,hi)
 {
     int H[] = { ,,,,,,,,,, };
     int size = hi - lo;
     int gap = max(H,,size);//选取小于规模的最大增量
     for (int t = gap; t >= ; t--)//从W[gap]一直到w=1，递减增量
     {
         int w = H[t];//选取步长,w即增量也是宽度(列数)
         for (int k = ; k < w; k++)//对于每一列
         {
             for (int i = lo + w; i < hi; i += w)//下面的循环即插入排序
             {
                 int j = i - w;
                 int tmp = A[i];
                 while ((j >= lo) && (A[j] > tmp))
                 {
                     A[j + w] = A[j];
                     j -= w;
                 }
                 A[j + w] = tmp;
             }//一列的插入排序结束
         }//每列都进行插入排序
     }
 }

希尔排序的总体策略，就是通过按列排序，使得每次排序后的局部有序性增加，最后达到全序列排序的目的。具体的证明可以参考《数据结构C++语言版》，有比较详细的h-有序和(g,h)-有序以及有序性增加的介绍。

下面是一个n=12，w{1,5}的过程。可以看到，w=5排序过后，有序性确实会有一定增加。

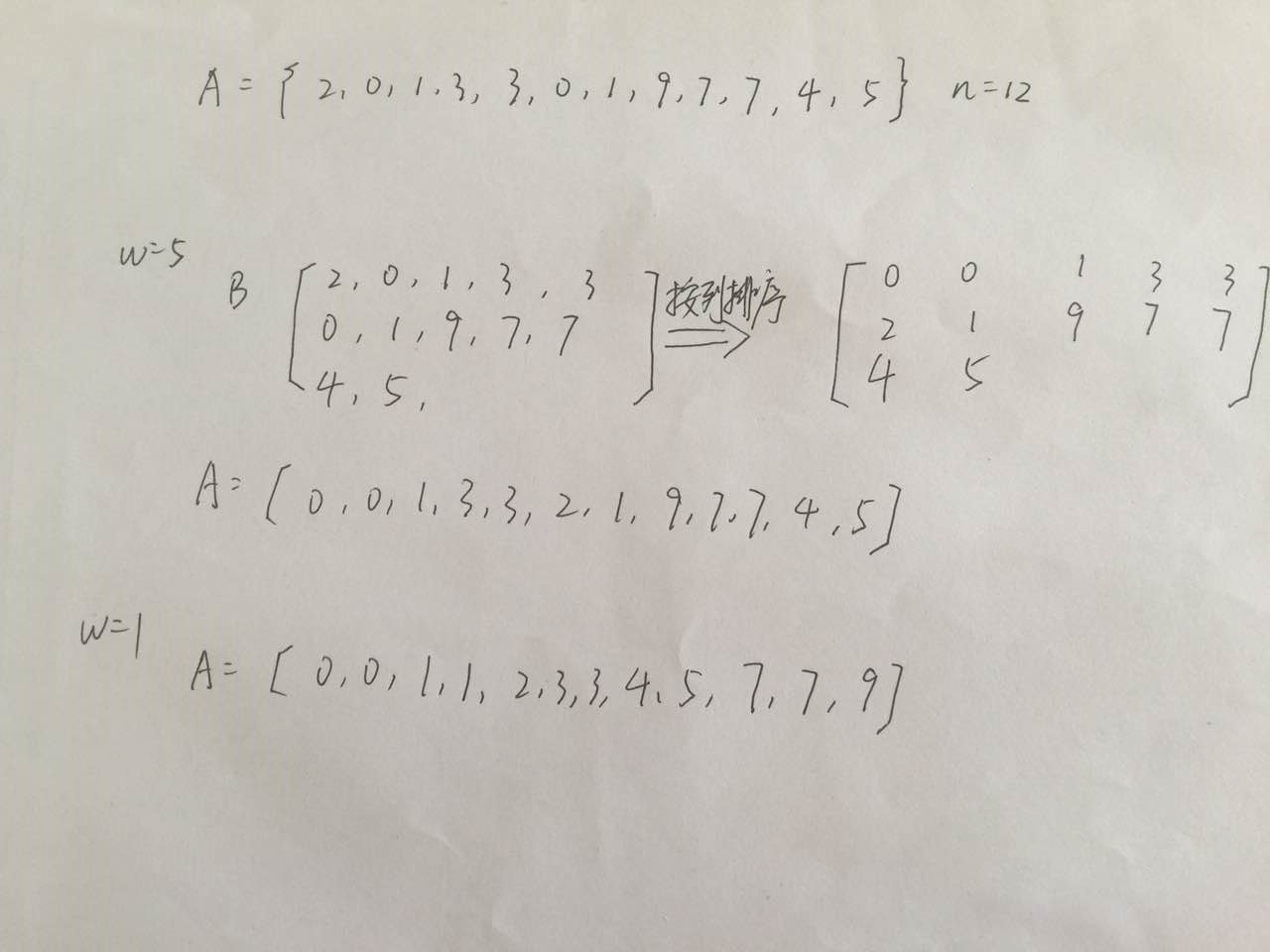
希尔排序的复杂度，取决于增量序列w的选择。几个比较优秀的序列，Pratt序列{1,2,3,4,6,8,9,12,..2^p*3^q,...}。这个序列的缺点很明显，会造成排序迭代次数很多，不过时间复杂度可以达到O(nlog^2n)。Sedgewick序列{1,5,19,41,109,209,505,929,2161,3905,8929...}的时间扶再度在最坏情况下可以为O(n^(4/3))，最好情况下为O(n^(7/6).