AtCoder Grand Contest 001 D - Arrays and Palindrome

题目传送门：https://agc001.contest.atcoder.jp/tasks/agc001_d

题目大意：

现要求你构造两个序列\(a,b\)，满足：

• \(a\)序列中数字总和为\(N\)
• \(b\)序列中数字总和为\(N\)
• \(a,b\)中包含的数都是正整数
• 满足以下两个条件的序列，所有元素必定相同
  • 最开始的\(a_1\)个元素是回文的，之后的\(a_2\)个元素是回文的，...，之后的\(a_n\)个元素是回文的
  • 最开始的\(b_1\)个元素是回文的，之后的\(b_2\)个元素是回文的，...，之后的\(b_n\)个元素是回文的

现在已知\(a\)为给定序列\(A\)的排列，请求出一组可能的序列\(a,b\)；若不存在，则输出\(Impossible\)

---

又是一个很妙的构(zhi)造(shang)题，如果满足那俩神奇条件，画一下长得就和蚊香一样

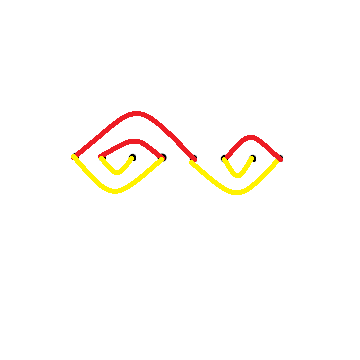
多打几个表就能发现，长度为奇数的回文串只能放在队首或队尾，而且超过两个就无解……然后为了扭成一个蚊香样，\(b\)串就需要满足第一个+1，最后一个-1，其余照抄即可

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
	static char buf[1000000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int frd(){
	int x=0,f=1; char ch=gc();
	for (;ch<'0'||ch>'9';ch=gc())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=gc())	x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline int read(){
	int x=0,f=1; char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x<0)	putchar('-'),x=-x;
	if (x>9)	print(x/10);
	putchar(x%10+'0');
}
const int N=1e2;
int A[N+10];
int main(){
	int n=read(),m=read(),cnt=0;
	for (int i=1;i<=m;i++)	A[i]=read(),cnt+=A[i]&1;
	if (cnt>2){
		printf("Impossible\n");
		return 0;
	}
	for (int i=1;i<=m;i++)	if (A[i]&1)	swap(A[1]&1?A[m]:A[1],A[i]);
	if (m==1){
		if (A[1]==1){
			printf("1\n1\n1\n");
			return 0;
		}
		printf("%d\n2\n1 %d\n",A[1],A[1]-1);
		return 0;
	}
	for (int i=1;i<=m;i++)	printf("%d",A[i]),putchar(i==m?'\n':' ');
	printf("%d\n%d ",m-(A[m]==1),A[1]+1);
	for (int i=2;i<m;i++)	printf("%d ",A[i]);
	if (A[m]!=1)	printf("%d\n",A[m]-1);
	return 0;
}