使用缓存方式优化递归函数与lru_cache

一.递归函数的弊端

递归函数虽然编写时用很少的代码完成了庞大的功能，但是它的弊端确实非常明显的，那就是时间与空间的消耗。

用一个斐波那契数列来举例

import time

#@lru_cache(20)
def fibonacci(n):
    if n < 2:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

t1 = time.time()
print(fibonacci(35))
t2 = time.time()
print(t2 - t1)  # 4.007285118103027
t1 = time.time()
print(fibonacci(36))
t2 = time.time()
print(t2 - t1)  # 6.479698419570923

前面输入的数较小，所以算的还算很快，但输入到35、36来测试时已经要花上好几秒来计算了，而且36比35计算时间多了两秒多，可想而知数据再增大后消耗的时间增加的是越来越大的，因为这个递归函数的复杂性是O(2**n)

我们想一下这个函数递归的原理，流程，发现一个问题，计算fibonacci(35)的时候，是计算fibonacci(34)+fibonacci(33)的和，计算fibonacci(34)时，是计算的fibonacci(33)+fibonacci(32)的和，问题出现了，fibonacci(33)需要计算两次，那不是重复了嘛，我们继续递归向下拆分发现，几乎所有的递归函数拆分为两个函数的和时都会有重复计算，就想下面这个图：

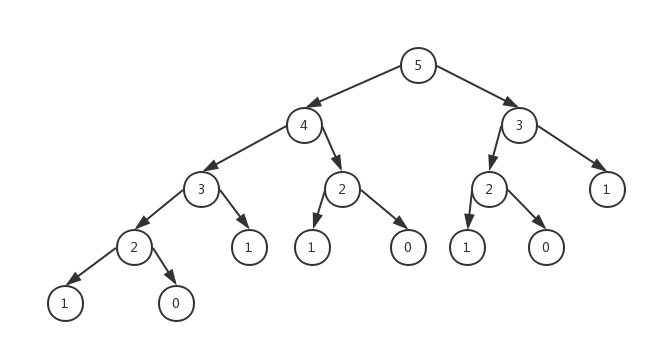
以fibonacci(5)举例，这个图里面有一大部分的数字是重复的，也就是说执行了很多的重复的函数，这使我们产生了一个想法，既然重复执行了，那我让它直接返回之前执行时的返回值不就行了，至于之前执行时的返回值，给他存起来不就好了吗，这就用到了我们下面要说的缓存思想

二.用缓存优化递归函数

我们定义一个装饰器来做函数的缓存

import time

def cache_decorator(func):
    cache_dict = {}

    def decorator(arg):
        try:
            return cache_dict[arg]
        except KeyError:
            return cache_dict.setdefault(arg, func(arg))
    return decorator

@cache_decorator
def fibonacci(n):
    if n < 2:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

t1 = time.time()
print(fibonacci(35))
t2 = time.time()
print(t2 - t1)  # 0
t1 = time.time()
print(fibonacci(36))
t2 = time.time()
print(t2 - t1)  # 0

当使用了缓存的方式后，发现计算所用的时间已经接近0，我们把数再改大一点

t1 = time.time()
print(fibonacci(300))
t2 = time.time()
print(t2 - t1)  # 0.001026153564453125
t1 = time.time()
print(fibonacci(301))
t2 = time.time()
print(t2 - t1)  # 0.0

这也太厉害了，当把数增大到300时，花费的时间才是0.001秒，而且t2的计算结果为0也证明了的确装饰器中缓存了数据，计算fibonacci(301)可直接从缓存中拿fibonacci(300)和fibonacci(299)，我们用图来更清晰的解释

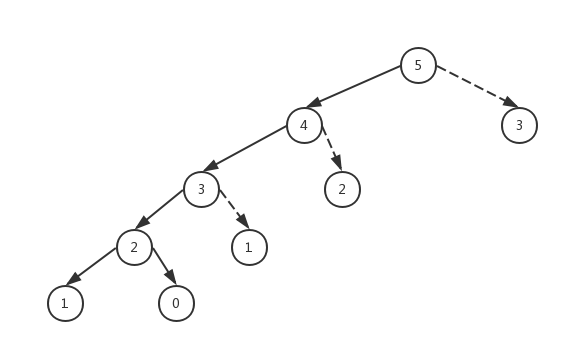
图中用虚线所指的结点都不需要重新计算了，只计算了不重复的数字，也就是意味着复杂度从O(2**n)降到了O(n)

这种缓存的思想，给我们的优化带来了巨大的收益

三.lru_cache装饰器

上面的装饰器是我们自己写的，但它不适用与其他函数，比如有多个参数的函数，但是python标准库为我们提供了一个非常方便的装饰器来进行缓存

它是functools模块中的lru_cache(maxsize,typed)

通过其名就能让我们了解它，它是通过lru算法来进行缓存内容的淘汰，

maxsize参数设置缓存内存占用上限，其值应当设为2的幂，值为None时表示没有上限

typed参数设置表示不同参数类型的调用是否分别缓存，这个参数的意思是如果设置为True，那么fibonacci(5)和fibonacci(5.0)将分别缓存，不存为一个。

lru_cache的使用只需要将上面我们自定义的装饰器替换为 lru_cache(None,False)即可。

---

参考《python高级编程（第2版）》

​