jdk1.8 HashMap红黑树操作详解-putTreeVal()

以前也看过hashMap源码不过是看的jdk1.7的，由于时间问题看的也不是太深入，只是大概的了解了一下他的基本原理；这几天通过假期的时间就对jdk1.8的hashMap深入了解了下，相信大家都是对红黑树和hashMap的扩容机制resize()比较感兴趣，红黑树也是jdk1.8对hashMap新加的一种数据结构，单纯的树形结构挺简单的，不过红黑树是一种自动保持平衡的树形结构，那就比较复杂了，可以通过我另一个博客可以先看一下红黑树的原理再看hashMap中的红黑树就简单多了连接<<<<<，hashMap的扩容机制resize()连接<<<<，废话不多说看代码（一些解释都在代码中）

 /**
     * 插入树形类型的元素
     * Tree version of putVal.
     *
     * 操作：将插入节点的hash值与每个节点的hash值进行比较，
     * 如果是小于那下一次插入节点就与当前节点的左子节点比，反之则与右子节点比，
     * 直到当前节点的（左或右）子节点为null，将其插入；
     * 每当插入一次节点都会调用一次方法balanceInsertion(root, x)将红黑树进行一个平衡操作
     */
    final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                                   int h, K k, V v) {
        Class<?> kc = null;
        boolean searched = false;
        //获取树的根节点
        TreeNode<K,V> root = (parent != null) ? root() : this;
        for (TreeNode<K,V> p = root;;) {
            int dir, ph; K pk;
            //h：插入节点的hash值
            //p：遍历到的当前节点
            if ((ph = p.hash) > h)
                dir = -1;
            else if (ph < h)
                dir = 1;
            else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                return p;
            else if ((kc == null &&
                      (kc = comparableClassFor(k)) == null) ||
                     (dir = compareComparables(kc, k, pk)) == 0) {
                if (!searched) {
                    TreeNode<K,V> q, ch;
                    searched = true;
                    if (((ch = p.left) != null &&
                         (q = ch.find(h, k, kc)) != null) ||
                        ((ch = p.right) != null &&
                         (q = ch.find(h, k, kc)) != null))
                        return q;
                }
                dir = tieBreakOrder(k, pk);
            }

            TreeNode<K,V> xp = p;
            if ((p = (dir <= 0) ? p.left : p.right) == null) {
                Node<K,V> xpn = xp.next;
                TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
                if (dir <= 0)
                    xp.left = x;
                else
                    xp.right = x;
                xp.next = x;
                x.parent = x.prev = xp;
                if (xpn != null)
                    ((TreeNode<K,V>)xpn).prev = x;
                //balanceInsertion(root, x):此方法是对红黑树进行平衡操作
                moveRootToFront(tab, balanceInsertion(root, x));
                return null;
            }
        }
    }

    /**
     * 插入元素 平衡红黑树的方法
     *
     * 注：不管遇到一下三种情况任意一种情况就会进行平衡调整 ，反之不需要；如果x节点是第1种情况，必然会经历2，3；如果x节点是第3种情况不会经历1，2；
     *
     * 1. 插入节点的父节点和其叔叔节点（祖父节点的另一个子节点）均为红色的；
     *
     * 2. 插入节点的父节点是红色，叔叔节点是黑色，且插入节点是其父节点的右子节点；
     *
     * 3. 插入节点的父节点是红色，叔叔节点是黑色，且插入节点是其父节点的左子节点。
     *
     * @param root
     * @param x
     * @return
     */
    static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) {
        //将插入的节点涂成红色
        x.red = true;
        //此时x节点是刚插入的节点
        // 这些变量名不是作者随便定义的都是有意义的。
        // xp：x parent，代表x的父节点。
        // xpp：x parent parent，代表x的祖父节点
        // xppl：x parent parent left，代表x的祖父的左节点。
        // xppr：x parent parent right，代表x的祖父的右节点。
        for (TreeNode<K, V> xp, xpp, xppl, xppr;;) {
            //如果x.parent==null证明x是根节点，并将x（根节点）返回；平衡完毕。
            if ((xp = x.parent) == null) {
                //将根节点涂成黑色
                x.red = false;
                return x;
            //只要进入此if就不会满足注释中3条件的任意一个，直接将root返回；平衡完毕。
            } else if (!xp.red || (xpp = xp.parent) == null)
                return root;
            //若父节点是祖父节点的左子节点，与下面的完全相反，本质是一样的
            if (xp == (xppl = xpp.left)) {
                //x节点的祖父节点的右子节点（叔叔节点）不为null且是红色，父节点必然也是红色，此时满足第1种情况。
                //操作：1.将祖父节点的右子节点（叔叔节点）、父节点涂为黑色
                //     2.将祖父节点涂为红色
                //     3.将祖父节点赋给x（参照节点的变更）
                if ((xppr = xpp.right) != null && xppr.red) {
                    xppr.red = false;
                    xp.red = false;
                    xpp.red = true;
                    x = xpp;
                //进入else 说明已经是第2或第3种情况了
                } else {
                    //第2种情况
                    // 操作：1.标记节点变为x。
                    //        2.左旋
                    //      3.x的父节点、x的祖父节点随之变化
                    if (x == xp.right) {
                        root = rotateLeft(root, x = xp);
                        xpp = (xp = x.parent) == null ? null : xp.parent;
                    }
                    //第3种情况
                    //操作 1.将父节点涂黑
                    //    2.祖父节点涂红
                    //    3.右旋
                    if (xp != null) {
                        xp.red = false;
                        if (xpp != null) {
                            xpp.red = true;
                            root = rotateRight(root, xpp);
                        }
                    }
                }
            } else {//若父节点是祖父节点的右子节点,与上面的完全相反，本质一样的
                if (xppl != null && xppl.red) {
                    xppl.red = false;
                    xp.red = false;
                    xpp.red = true;
                    x = xpp;
                } else {
                    if (x == xp.left) {
                        root = rotateRight(root, x = xp);
                        xpp = (xp = x.parent) == null ? null : xp.parent;
                    }
                    if (xp != null) {
                        xp.red = false;
                        if (xpp != null) {
                            xpp.red = true;
                            root = rotateLeft(root, xpp);
                        }
                    }
                }
            }
        }
    }

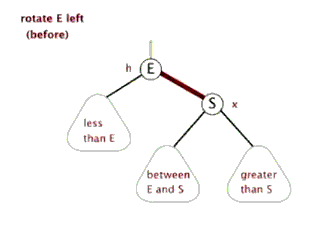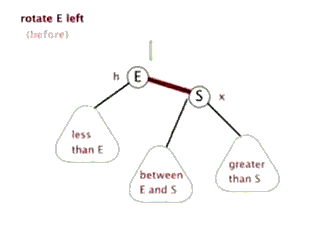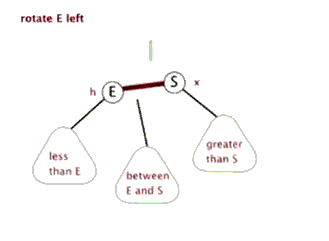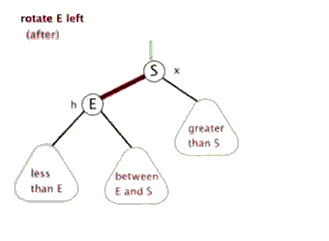
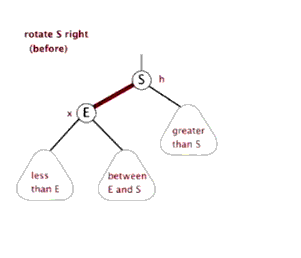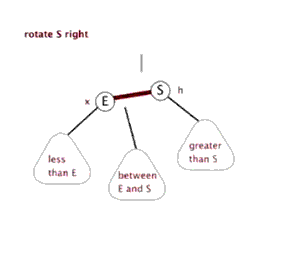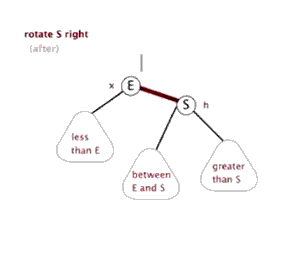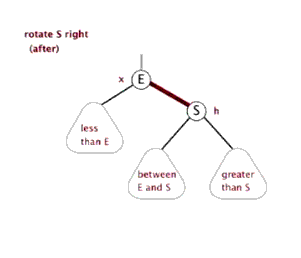
左旋和右旋只通过代码说，没有图听不明白，必须通过上边说的红黑树原理的那篇博客结合代码才容易看明白，先上一个那篇博客中的左旋和右旋的动态图先了解一下

左旋有个很萌萌哒的动态示意图，可以方便理解：

右旋也有个很萌萌哒的动态示意图，可以方便理解

hashMap的代码我就不贴了大家可以自己看一下