2.18比赛（T2，T3留坑）

2.18比赛（T2,T3留坑）

pdf版题面

pdf版题解

超越一切（ak）

【题目描述】

夏洛可得到一个(h+1)×(w+1)的巧克力，这意味着她横着最多可 以切 h 刀，竖着最多可以切 w 刀 她想总共切 k 刀，每刀要么竖着切要么横着切，如果竖着切了 i 刀，横着切了 j 刀，会得到(i+1) ×(j+1)个巧克力，定义一个切 k 刀 的方案的代价是每一刀切完后巧克力个数之和，假设每刀切的位置是 随机选择的（即剩余能切的位置等概率随机选一个），请你求出期望 代价，对10⁹+7 取模

【输入格式】

一行三个正整数 h,w,k

【输出格式】

一行一个整数表示答案

【样例 1 输入】

2 1 2

【样例 1 输出】

666666677

【数据范围】

本题有 6 个子任务，每个子任务只有 1 个测试点

对于 100%的数据，满足 h,w≤ 10¹⁸,k≤h+w

Subtask 1[10 pts]: h,w≤300

Subtask 2[10 pts]:h,w≤5000

Subtask 3[30 pts]:h,w≤10⁶

Subtask 4[25 pts]:k≤10⁷

Subtask 5[15 pts]:k=h+w

Subtask 6[10 pts]:无特殊限制 选手文件夹下的额外样例和最终数据范围相同

sol：题解写的非常好（大雾）

稍微解释一下，对于每一个矩形，只对它左下角的那个点记录贡献

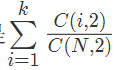记录的是中间的点的贡献，就是不在边界上的点，这样的点共有h*w个，每个点切中的概率就是前面那个式子

然后因为这是每个点的期望，统计答案时要乘以h*w

还有边上的点，对于最最左下角的点,k刀中每次切都会有1的贡献，所以ans+k

还有不在左下角的点，每次切都会新产生一个会造成贡献的点，ans+=(1+k)*k/2

标算已经在上面了，在贴一遍没什么意思，放一份较易理解的75pts的暴力好了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+'');    return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const ll Mod=;
const ll N=;
ll h,w,k;
ll Jiec[N],Niy[N];
inline void Ad(ll &x,ll y)
{
    x+=y;
    x-=(x>=Mod)?(Mod):;
    return;
}
inline ll Ksm(ll x,ll y)
{
    ll ans=1ll;
    while(y)
    {
        if(y&) ans=ans*x%Mod;
        x=x*x%Mod;
        y>>=;
    }
    return ans%Mod;
}
inline ll C(ll n,ll m)
{
    if(!Niy[m]) Niy[m]=Ksm(Jiec[m],Mod-)%Mod;
    if(!Niy[n-m]) Niy[n-m]=Ksm(Jiec[n-m],Mod-)%Mod;
    return Jiec[n]*Niy[m]%Mod*Niy[n-m]%Mod;
}
int main()
{
    freopen("ak.in","r",stdin);
    freopen("ak.out","w",stdout);
    ll i;
    R(h); R(w); R(k);
    Jiec[]=1ll;
    for(i=;i<=h+w;i++)
    {
        Jiec[i]=Jiec[i-]*i%Mod;
    }
    ll ans=;
    ll NN=Ksm(C(h+w,2ll),Mod-)%Mod;
    Ad(ans,C(k + ,3ll)*NN%Mod);
    ans=ans*(h*w%Mod)%Mod;
    Ad(ans,(((+k)*k)>>)%Mod);
    Ad(ans,k);
    Wl(ans);
    return ;
}
/*
input
1 2
output
*/

75pts暴力

附上ak王pfy的题解