回溯算法_ BackTracking

 目前还存在的疑问：

1. 所谓的该分支满足条件之后就回退到上一层节点，可是加谁呢? x[i+1]  ??

加到 N， 不满足target sum条件就返回上一级（同时改变上一级数为 i+1...纵向继续从 i+1 加到++ N中间有满足的sum就返回组合，没有就一直加到N 自动结束，结束后再返回上一级 i+1。。。。。）

2. 可以通过提前排序的方法来优化这个算法

we can improve the above algorithm by strengthening the constraint checks and presorting the data；By sorting the initial array, we need not to consider rest of the array, once the sum so far is greater than target number. We can backtrack and check other possibilities.

3. Geek案例用的是后续遍历？

post order traversal

总感觉 37行这里不对：不应该是减去  sum - s[ite]， 应为在  47行加过 1 了  i+1 ？？？？？？？？？？？？？？？？？？？？？？？？？

38行这个 唯一的return我表示很费解？他前面的递归调用函数怎么走呢？？？

我一定要在java代码里把下面改为ite-1   否则怎么都解释不通：

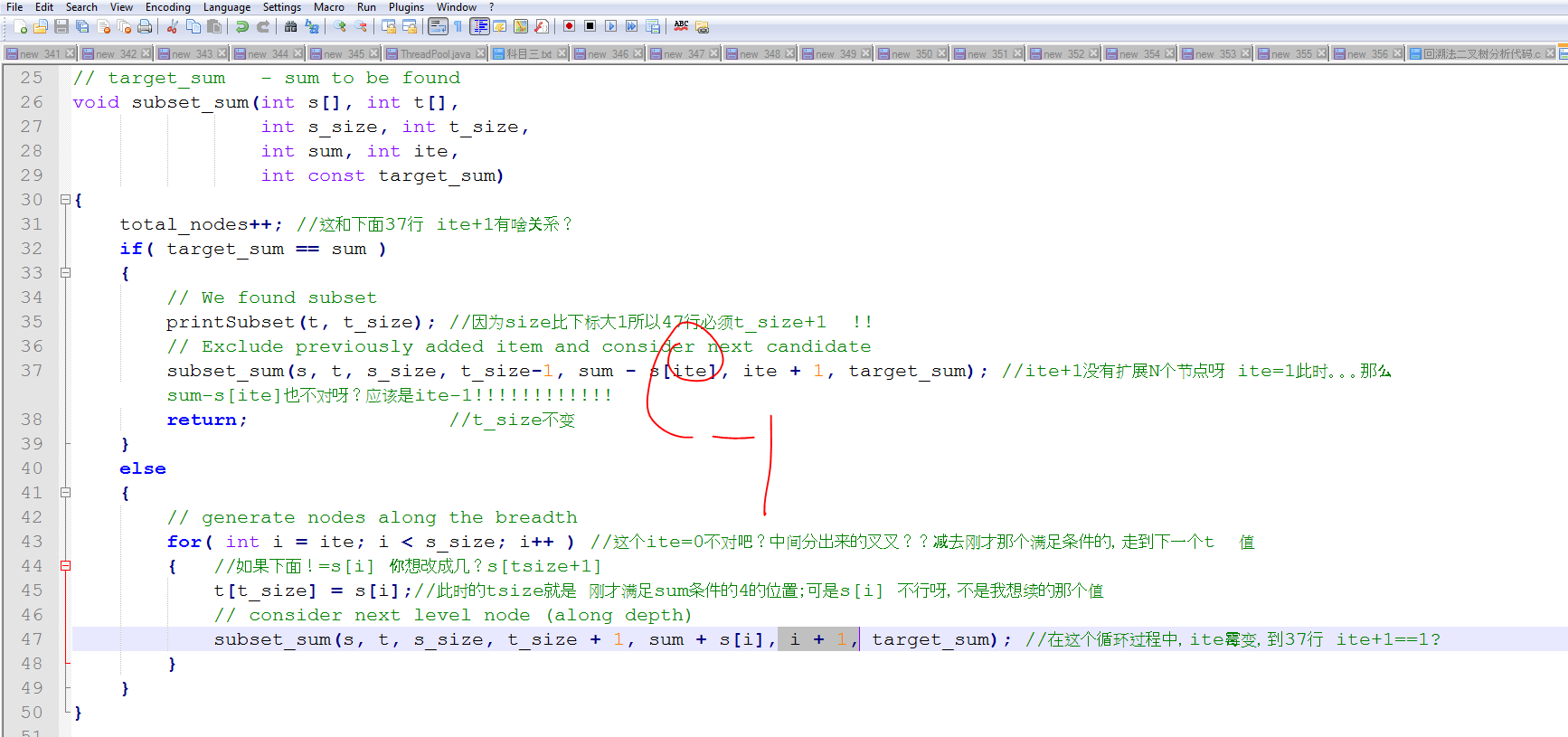
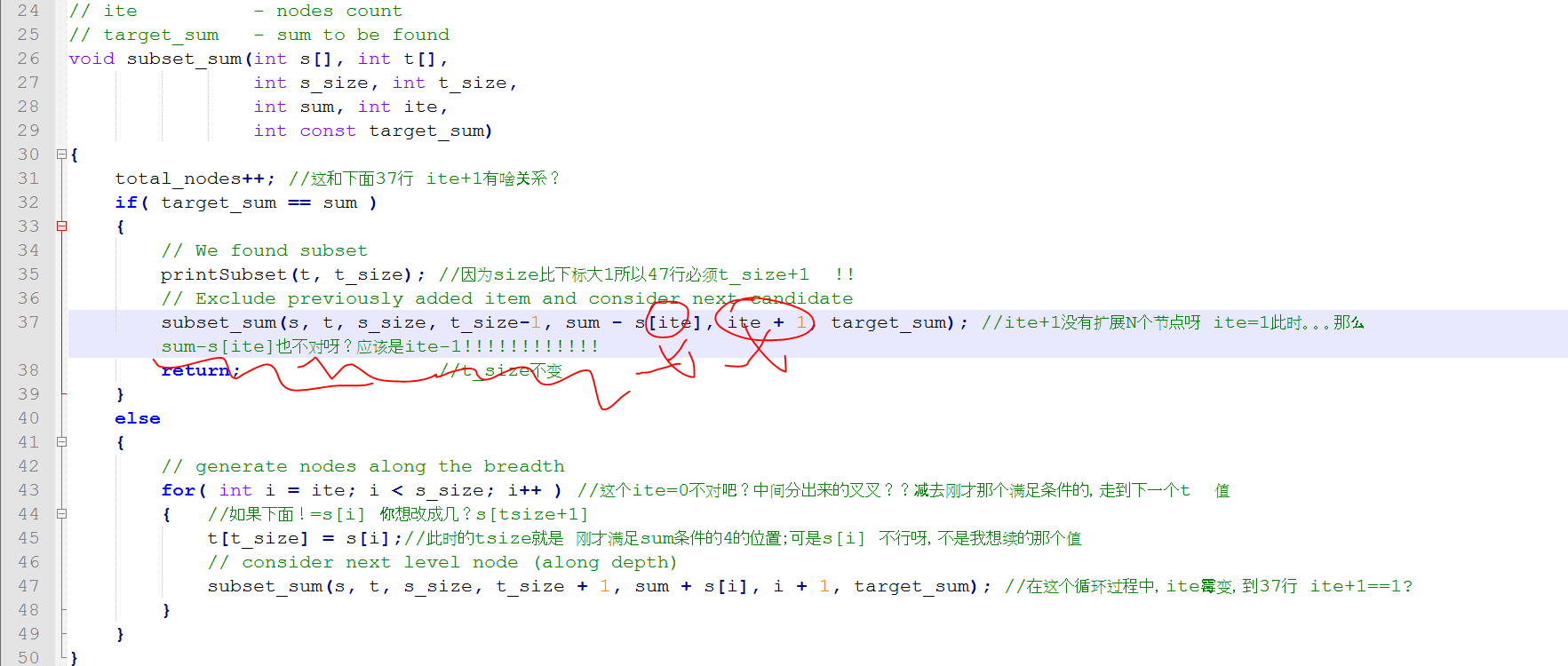
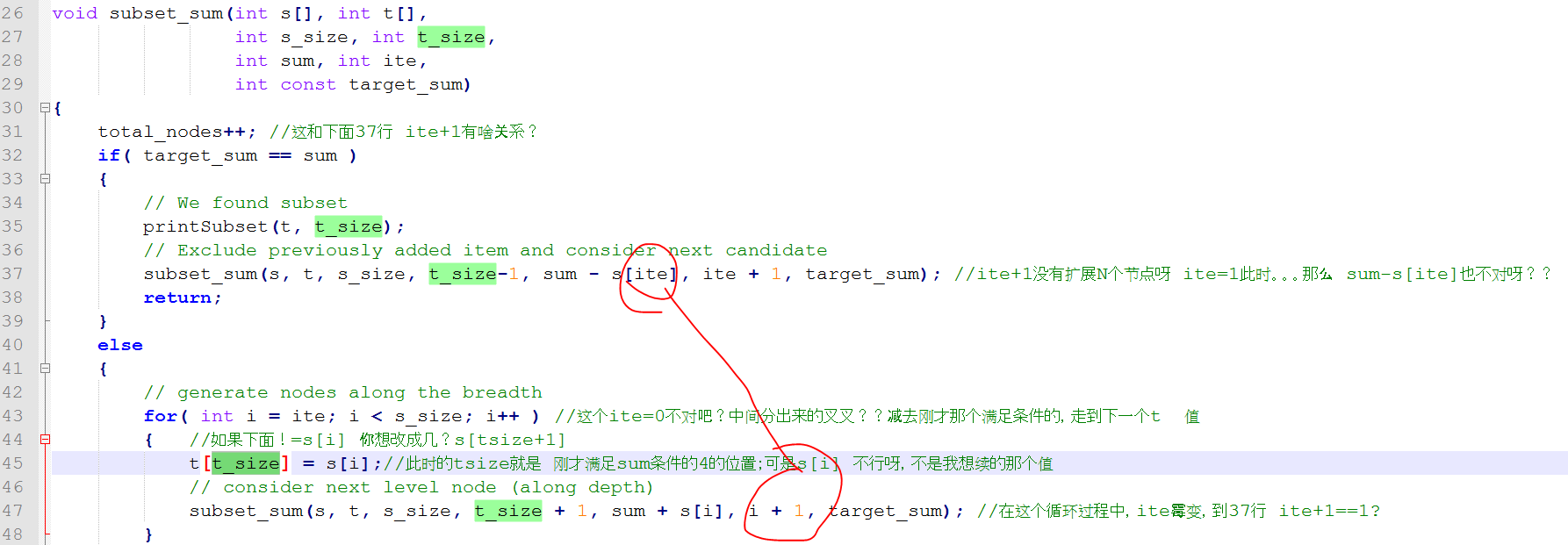
对的，因为 ite 和 i+1就是再同一个参数位置：

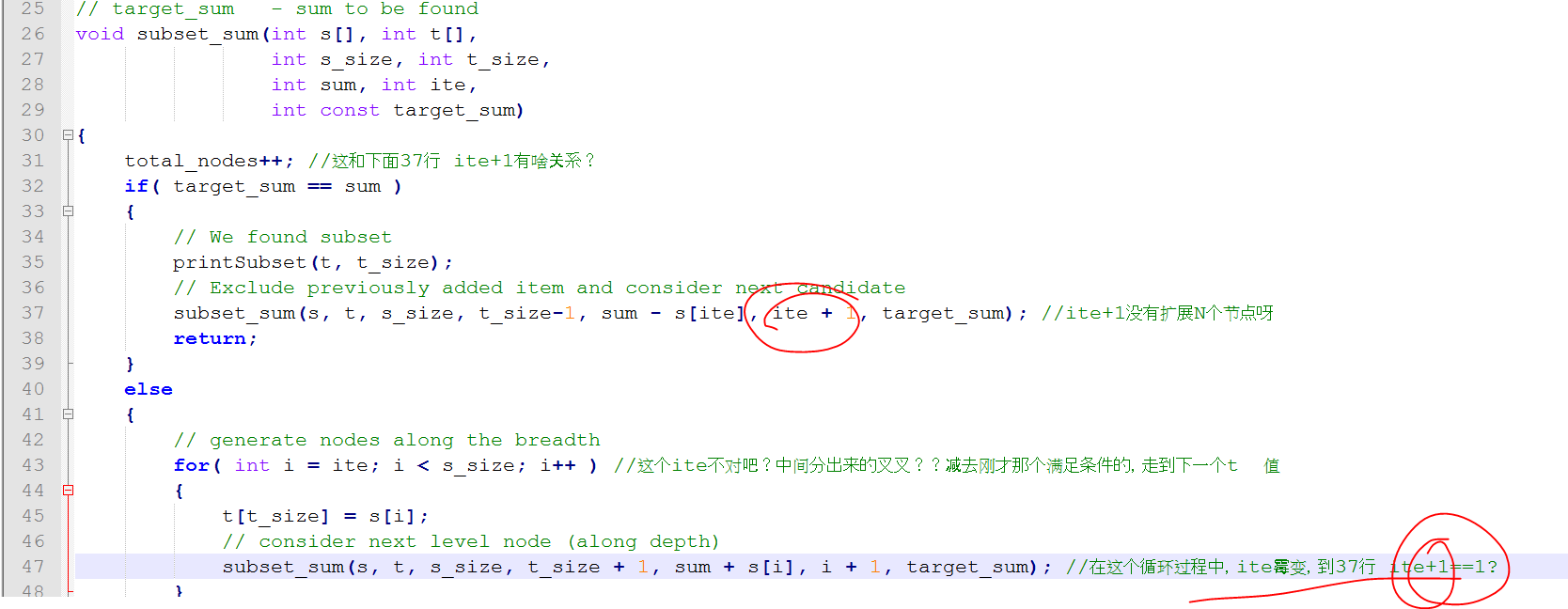
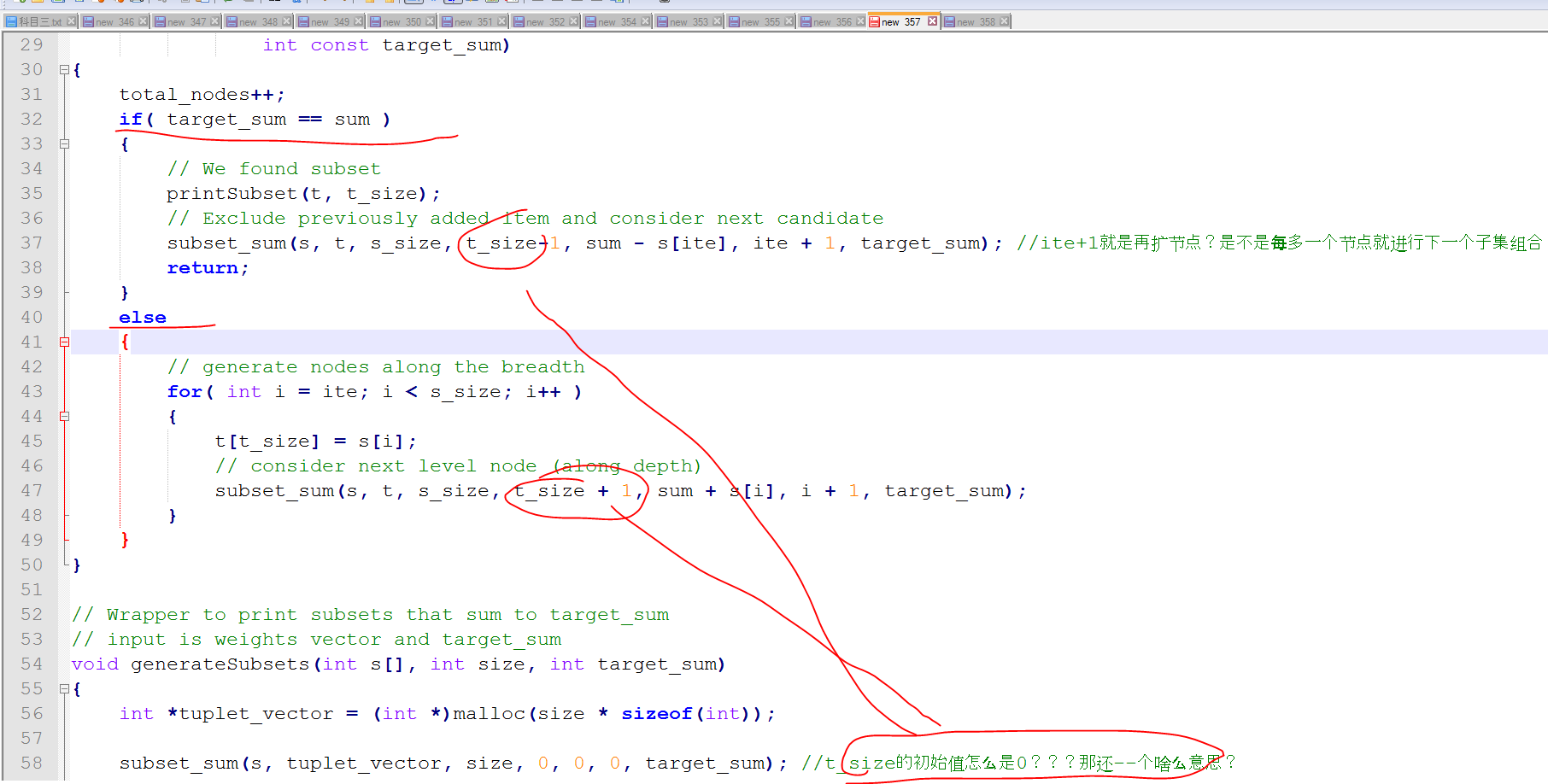
1. 看上图好像只有subset sum 符合条件采取增加节点：ite 而且直接return了，不再继续找子集？

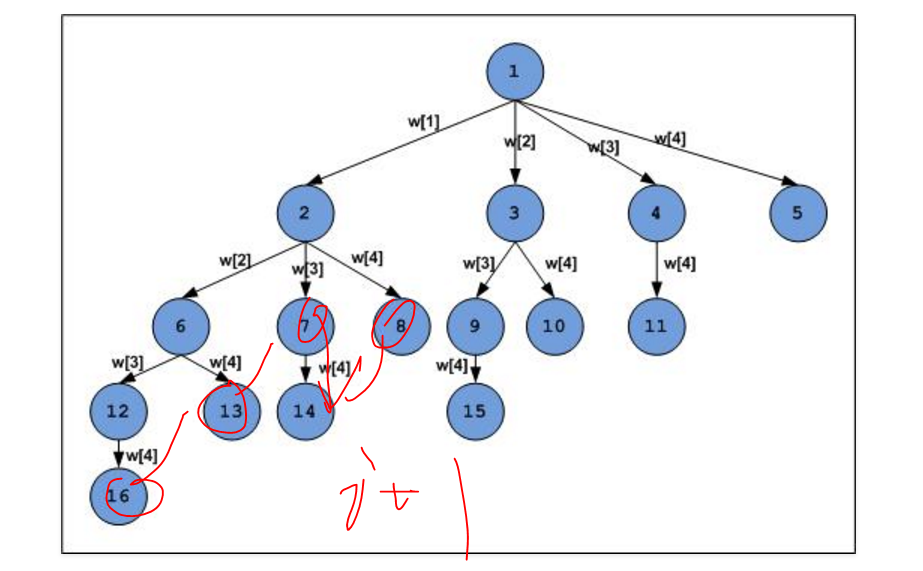
2. 关于这可二叉树的解释：

2.1

n the above tree, a node represents function call and a branch represents candidate element.

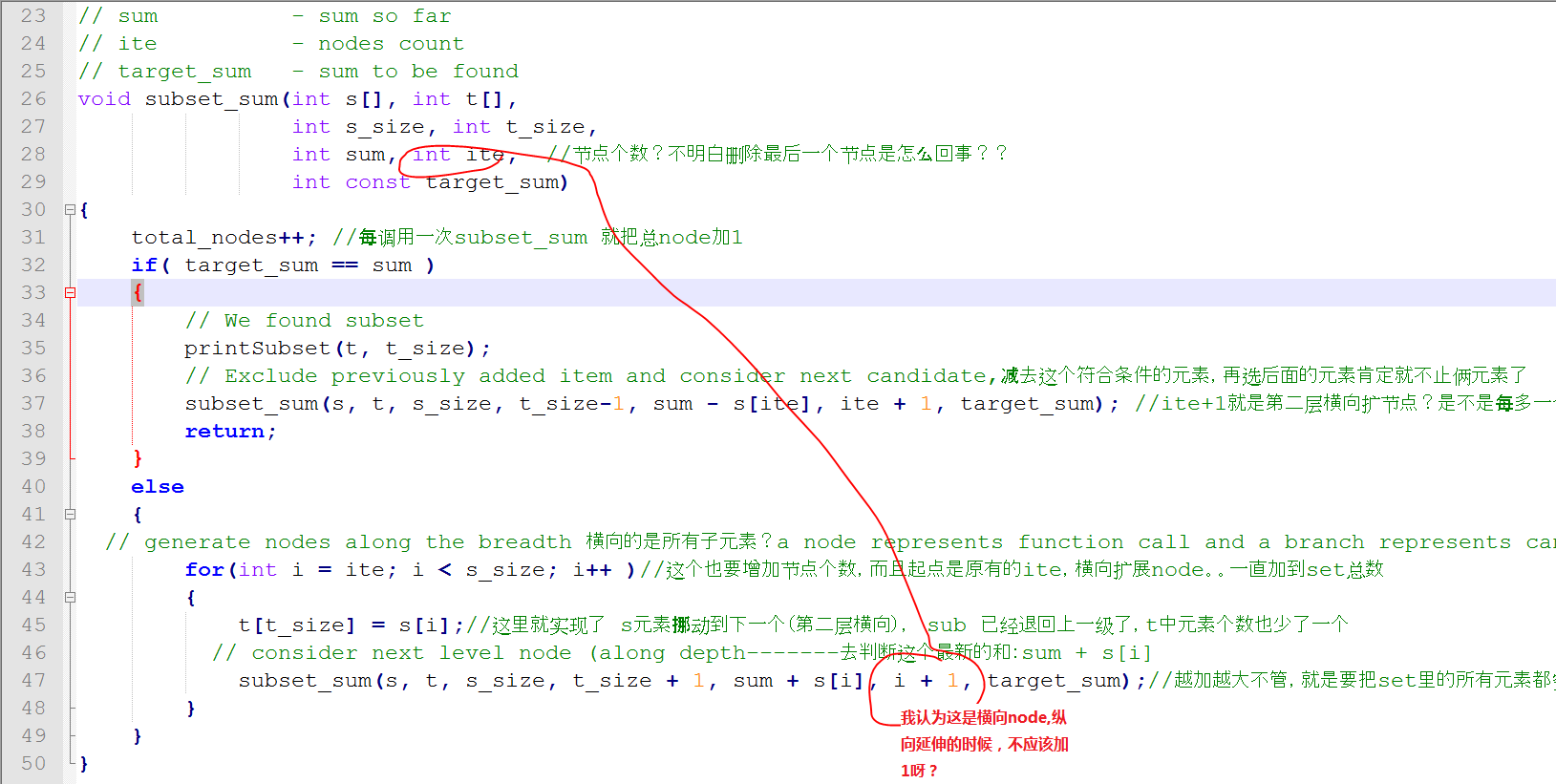
从下图可以看出来，横向是把s里的元素挨个走一遍，depth纵向是不断增加 subset里的元素个数，直到把set 里的所有元素都加入subset,即使我们知道越加越大已经超过了 target sum

if( target_sum == sum )
{
// We found subset
printSubset(t, t_size);
// Exclude previously added item and consider next candidate,减去这个符合条件的元素，再选后面的元素肯定就不止俩元素了
subset_sum(s, t, s_size, t_size-1, sum - s[ite], ite + 1, target_sum); //ite+1就是第二层横向扩节点？是不是每多一个节点就进行下一个子集组合
return;
}

我理解这是退回上一层, subset size退回上一级，可是元素s[i] 是怎么挪动的？如下图理解：

下图i+1有疑问：我就是认为这个t_size不应该+1  , 因为刚才已经回退了一层呀？？！！不对我理解错了，人家这样是对的；

我的新发现：那就是横向和纵向扩展其实都是在加s[i],   也就是s 里所有的元素都要试一遍，加到最后一个元素。注意那个for循环，我所考虑的，如果一个分支加到最后一个元素还是得不到target sum,那么就结束了for循环， 也不输出什么，也不return.....随着循环的结束而结束程序。。。