C#树类型及其遍历

最近有个项目不仅需要取部门的层级关系，还要处理不规则的关系（移除某个部门），只有树结构才能实现相关遍历和操作。

涉及到的知识点：泛型、递归、数据结构

既然研究树类型就先来看下树的定义：

一棵树（tree）是由n（n>0）个元素组成的有限集合，其中：

（1）每个元素称为结点（node）；

（2）有一个特定的结点，称为根结点或根（root）；

（3）除根结点外，其余结点被分成m（m>=0）个互不相交的有限集合，而每个子集又都是一棵树（称为原树的子树）；——百度

本文将简化树，只研究树的结点-结点树。结点树包含：父结点（根结点的父结点为null）、子结点（List集合）、数据对象。

类的设计：

public class BoTree<T>
    {
        public BoTree()
        {
            nodes = new List<BoTree<T>>();
        }

        public BoTree(T data)
        {
            this.Data = data;
            nodes = new List<BoTree<T>>();
        }

        private BoTree<T> parent;
        /// <summary>
        /// 父结点
        /// </summary>
        public BoTree<T> Parent
        {
            get { return parent; }
        }
        /// <summary>
        /// 结点数据
        /// </summary>
        public T Data { get; set; }

        private List<BoTree<T>> nodes;
        /// <summary>
        /// 子结点
        /// </summary>
        public List<BoTree<T>> Nodes
        {
            get { return nodes; }
        }
        /// <summary>
        /// 添加结点
        /// </summary>
        /// <param name="node">结点</param>
        public void AddNode(BoTree<T> node)
        {
            if (!nodes.Contains(node))
            {
                node.parent = this;
                nodes.Add(node);
            }
        }
        /// <summary>
        /// 添加结点
        /// </summary>
        /// <param name="nodes">结点集合</param>
        public void AddNode(List<BoTree<T>> nodes)
        {
            foreach (var node in nodes)
            {
                if (!nodes.Contains(node))
                {
                    node.parent = this;
                    nodes.Add(node);
                }
            }
        }
        /// <summary>
        /// 移除结点
        /// </summary>
        /// <param name="node"></param>
        public void Remove(BoTree<T> node)
        {
            if (nodes.Contains(node))
                nodes.Remove(node);
        }
        /// <summary>
        /// 清空结点集合
        /// </summary>
        public void RemoveAll()
        {
            nodes.Clear();
        }
    }

测试：

首先创建一个学生类（任意）

public class Student
    {
        public Student(string name, string sex, int age)
        {
            this.Name = name;
            this.Sex = sex;
            this.Age = age;
        }
        public string Name { get; set; }
        public string Sex { get; set; }
        public int Age { get; set; }
    }

初始化树：

BoTree<Student> tree1 = new BoTree<Student>();
tree1.Data = new Student("小波1", "男", );

BoTree<Student> tree2 = new BoTree<Student>();
tree2.Data = new Student("小波2", "男", );

BoTree<Student> tree3 = new BoTree<Student>();
tree3.Data = new Student("小波3", "男", );

BoTree<Student> tree4 = new BoTree<Student>();
tree4.Data = new Student("小波4", "男", );

tree1.AddNode(tree2);
tree1.AddNode(tree3);
tree3.AddNode(tree4);

调试：

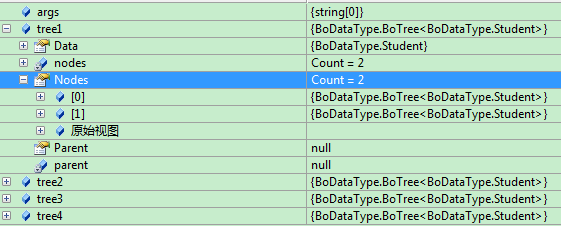
可以从监视中看出tree1有2个子结点

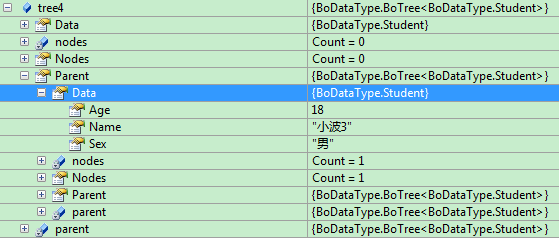
可以看出tree4的父结点为tree3

下面我们来遍历这棵树：

public static void Recursive(BoTree<Student> tree)
        {
            Console.WriteLine("姓名：{0}，姓名：{1}，年龄：{2}", tree.Data.Name, tree.Data.Sex, tree.Data.Age);
            if (tree.Nodes.Count > )
            {
                foreach (var item in tree.Nodes)
                {
                    Recursive(item);
                }
            }
        }

调用结果：

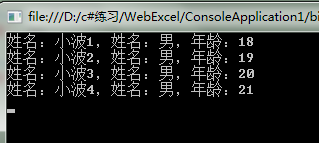
需要说明的是：不要尝试用Nodes.Add(T item)来添加结点，而是用AddNode方法来添加结点。AddNode方法将对Parent进行赋值，保证了父结点可查询