[算法] Manacher算法线性复杂度内求解最长回文子串

参考：http://www.felix021.com/blog/read.php?2040

以上参考的原文写得很好，解析的非常清楚。以下用我自己的理解，对关键部分算法进行简单的描述：

• 回文的判断需要完成从中心字符向两侧进行逐字符匹配；
• 回文好比圆，由两个重要的参数决定，即“圆心”（中心字符，对偶数长的回文而言是两个字符）和“直径”（回文长度）；
• 如果一个“点”落入另一个“圆”内，则以这个点为圆心的“圆”必定受这个“大圆”及相对大圆圆心对称的“对称圆”的影响：
  • 在“大圆”范围内，这个“圆”的直径不能大于“对称圆”的直径（只要在大回文的范围内，该回文的字符匹配结果可以取用对称位置回文的匹配结果）；
  • 即使“对称圆”超出“大圆”边界，这个“圆”也不能超出“大圆”边界（如果对称位置回文长度超出了大回文范围，则该回文不可超出范围，否则大回文需要延展，即大圆需要扩张）；

盗两张图：

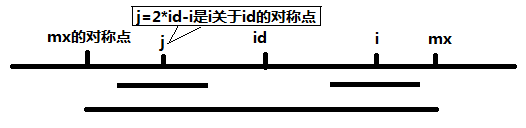
对称回文在大回文范围内

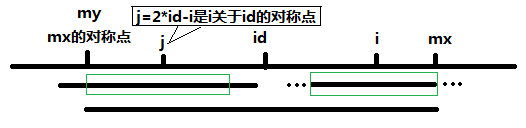
对称回文超出大回文范围

这个算法巧妙利用了回文的特点，在线性求解过程中充分利用了之前已得到的结果，尽量避免重复匹配，极大降低复杂度。

string = "12212321"
SEPCHAR = '#'

target = ""

# pre-process

for i in range(len(string)):
    target = target + SEPCHAR + string[i]

target=target + SEPCHAR

# the key procedure

idx = 0
mx = 0
p=[]

for i in range(len(target)):
    p.append(0)

for i in range(len(target)):
    if i >= mx:
        p[i] = 1
    else:
        p[i] = min(p[2*idx-i], mx-i)
    while (i+p[i]) in range(len(target)) and (i-p[i]) in range(len(target)) and target[i+p[i]] == target[i-p[i]]:
        p[i] += 1
    if (i + p[i] > mx):
        mx = i + p[i]
        idx = i

# print the results

print string

for i in range(len(target)):
    print target[i],

print ""

max_len = 0
center = 0

for i in range(len(target)):
    print p[i],
    if p[i] > max_len:
        max_len = p[i]
        center = i

print ""

print "max len of palindrom is %d at index %d" %(max_len-1, center/2)