机器学习中的矩阵方法04:SVD 分解
前面我们讲了 QR 分解有一些优良的特性,但是 QR 分解仅仅是对矩阵的行进行操作(左乘一个酉矩阵),可以得到列空间。这一小节的 SVD 分解则是将行与列同等看待,既左乘酉矩阵,又右乘酉矩阵,可以得出更有意思的信息。奇异值分解( SVD, Singular Value Decomposition ) 在计算矩阵的伪逆( pseudoinverse ),最小二乘法最优解,矩阵近似,确定矩阵的列向量空间,秩以及线性系统的解集空间都有应用。
1. SVD 的形式
对于一个任意的 m×n 的矩阵 A,SVD 将一个矩阵分解为三个特殊矩阵的乘积, 国外还做了一个视频——SVD 之歌:
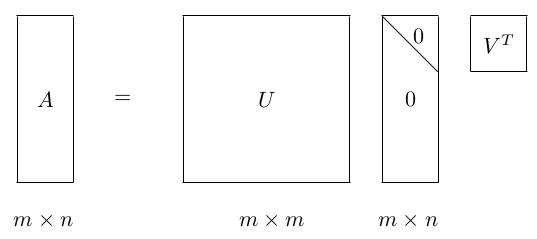
其中, U 和 是酉矩阵,
是对角线矩阵。注意酉矩阵只是坐标的转换,数据本身分布的形状并没有改变,而对角矩阵,则是对数据进行了拉伸或者压缩。由于 m
>= n,又可以写成下面这种 thin SVD 形式:
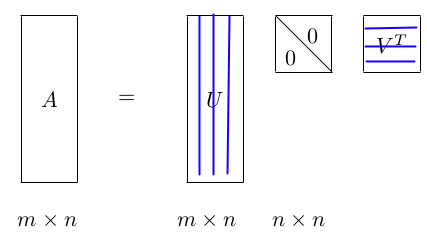
2. SVD 的几何解释
考虑 A 是 2×2 的简单情况。我们知道,一个几何形状左乘一个矩阵 A 实际上就是将该形状进行旋转、对称、拉伸变换等错切变换, A 就是所谓的 shear 矩阵。比如可以将一个圆通过左乘 A 得到一个旋转后的椭圆。
举个例子,假设 A 对平面上的一个圆进行变换:
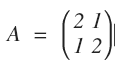
如果只看矩阵 A, 我们几乎无法直观看到圆是如何变换的。变换前的圆是:
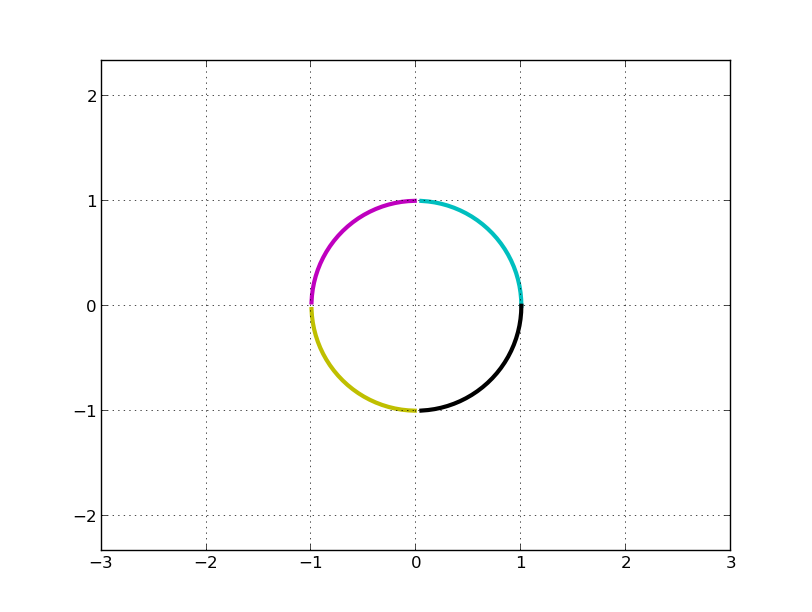
C, M, Y, K 分别表示第一、二、三、四象限。左乘 A 矩阵后得到:
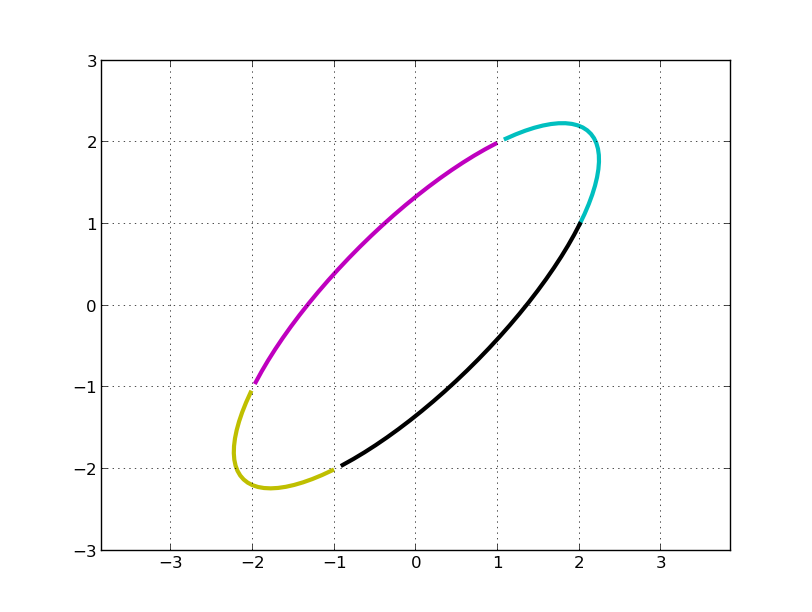
我们的问题是,旋转了多少度?伸缩的方向是多少?最大伸缩比例是多少?
利用这个在线工具对 A 进行 SVD 分解:
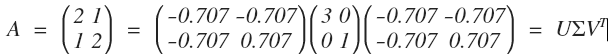
明显,我们看到 A 变换实际上是先对圆顺时针旋转 45°(可以看做是坐标轴逆时针宣战了 45°,主成分方向),再关于 x 轴对称(第一行乘以 -1), 即左乘 V^T:
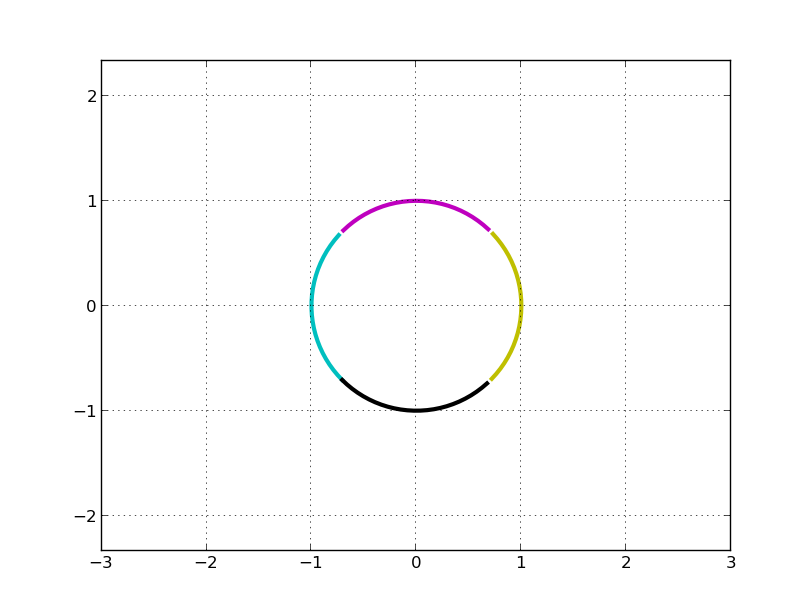
然后在 x 方向拉伸 3 倍(左乘S):
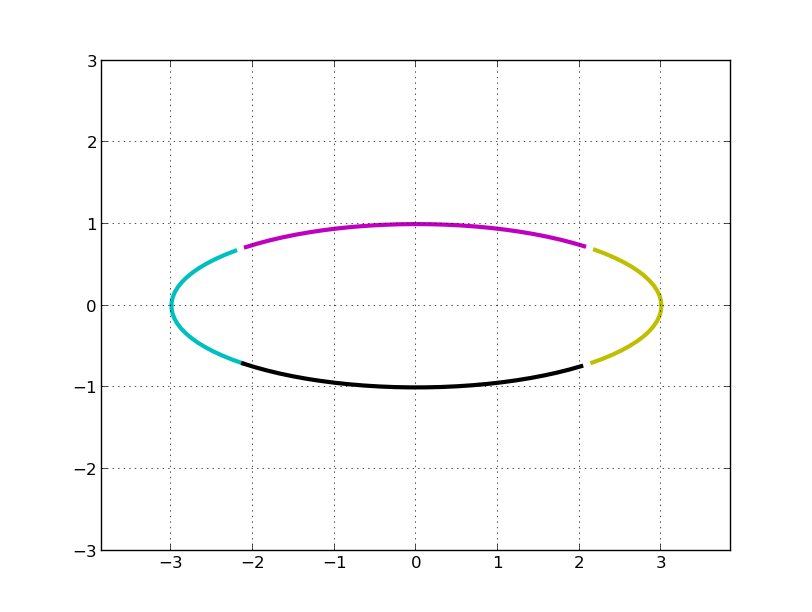
最后再顺时针旋转 45°,再关于 x 轴对称(第一行乘以 -1, 两次对称操作抵消了), 即左乘 U:
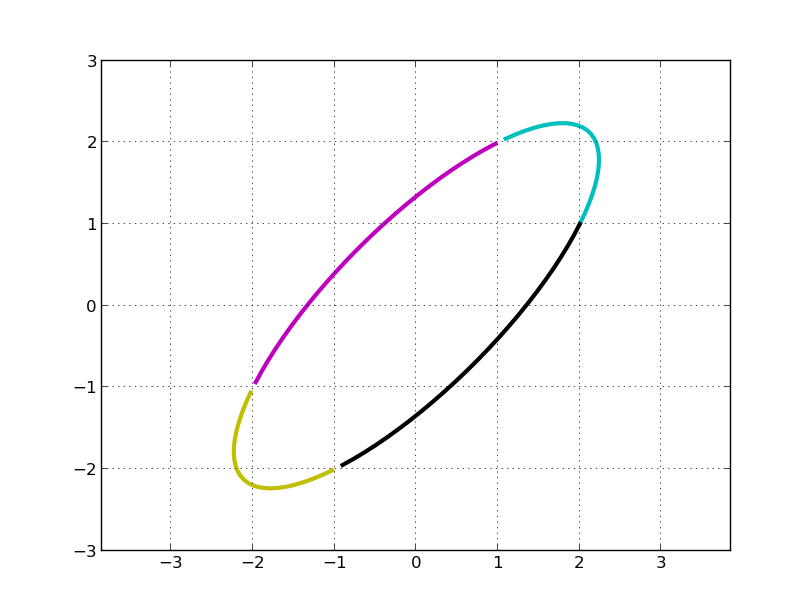
上述绘图过程的 python 代码如下:
# -*- coding=utf-8
#!/usr/bin/python2.7 from pylab import * def plotCircle(before, M=matrix([[1, 0], [0, 1]])):
'''before: 变换前的矩阵
M: 变换矩阵,默认为单位矩阵
返回变换之后的矩阵
'''
eclMat = M * before # M 变换
eclX = array(eclMat[0]).reshape(-1)
eclY = array(eclMat[1]).reshape(-1)
axis('equal')
axis([-3, 3, -3, 3])
grid(True)
plot(eclX[:25], eclY[:25], 'c', linewidth=3)
plot(eclX[25:50], eclY[25:50], 'm', linewidth=3)
plot(eclX[50:75], eclY[50:75], 'y', linewidth=3)
plot(eclX[75:100], eclY[75:100], 'k', linewidth=3)
show()
return eclMat ang = linspace(0, 2*pi, 100) x = cos(ang)
y = sin(ang)
cirMat = matrix([x, y]) # 2 × 100 的圆圈矩阵 # 画最开始的图形——圆
plotCircle(cirMat) # 画变换之后的椭圆
M = matrix([[2, 1], [1, 2]]) # 2 × 2 的变换矩阵
clMat = plotCircle(cirMat, M) # 将 M 矩阵进行 svd 分解
U, s, V = np.linalg.svd(M, full_matrices=True)
S = np.diag(s) # SVD 矩阵对圆的变换
plotCircle(cirMat)
Tran1 = plotCircle(cirMat, V)
Tran2 = plotCircle(Tran1, S)
Tran3 = plotCircle(Tran2, U)
3. SVD 向量空间
假设矩阵 A 的秩是 r, 那么对角线矩阵的秩也是 r (乘以酉矩阵不会改变矩阵的秩), 我们假设:

那么, Ax = 0 的 null space 也就是解空间是什么呢?答案如下:
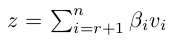
证明非常简单,直接带入 SVD 分解三个矩阵的右边,计算的时候正交的向量相乘都等于0, 不为 0 的恰好都被对角线矩阵的 0 元素归零,等号成立。如果 A 是列满秩的,显然符合条件的只剩下零向量了。同样的,你可以知道 A' 的 null space。矩阵 A 的线性子空间是啥?设想有一个很高的矩阵 A, 它的列向量很有可能不是正交的。对于任意一个坐标 x,矩阵 A 的线性子空间可以定义为:
R(A) = {y | y = Ax, x 是任意的坐标}
那么, u1, u2,..., ur 是 R(A) 的正交基。
这个想法也非常直观,无论来了一个什么向量(或者叫坐标), 经过 V^T 和 对角线矩阵变换之后还是一个坐标,这个坐标就是 U 矩阵列向量线性组合的系数。
4. SVD 的计算
这就是正定矩阵的对角化。计算过程如下:
- 计算 A' (A 的转置)和 A'A
- 计算 A'A 的特征值,将特征值按照递减的顺序排列, 求均方根,得到 A 的奇异值
- 由奇异值可以构建出对角线矩阵 S, 同时求出 S 逆,以备后面的计算
- 有上述排好序的特征值可以求出对应的特征向量,以特征向量为列得到矩阵 V, 转置后得到 V'
- U = AVS逆,求出 U,完毕。
Lanczos algorithm 是一种迭代的计算方法,没来得及细看。
感觉 SVD 计算水很深,要用到的时候再看,现在暂不深入了。
5. PCA
主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。假设上面的椭圆中(二维空间,两个坐标值)均匀分布了非常多的点,如何在一维空间(一个坐标值)里面就能最大程度将这些点区分开来呢?这时候就要用到 PCA:

可以看到,上图中将所有的点投影到 +45° 直线上,将二维空间映射到一维空间,可以最大程度地区分开这些点,即投影后的样本分布方差最大,这个方向就是 v1 向量的方向。就上图来说,假设 100×2 的矩阵 X 表示样本点在平面上的坐标,将这些点投影到 v1 上保留最大的样本方差:
这样,就将 100 个 2 维空间的样本点压缩为 100 个 1 维空间的样本点,这里的列压缩实际上是对特征进行了压缩, 而不是简单地丢弃。PCA 是不是只能在样本点个数大于特征个数的时候才能压缩呢?例如,现在 3 个 100 维特征的样本用 100×3 的矩阵表示,用 SVD 分解后可以得到三个矩阵的乘积,做如下变换:
同样也最大限度保留了主成分。
总结起来,一个矩阵 A, 如果想对行进行压缩并保留主成分,那么左乘 u1', 如果相对列进行压缩并保留主成分(让我联想起了稀疏表示),那么右乘 v1。
当然,上面是简单的保留第一个主成分,PCA的全部工作简单点说,就是对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴是使得方差最大的,第二个轴是在与第一个轴正交的平面中使得方差最大的,第三个轴是在与第1、2个轴正交的平面中方差最大的,这样假设在N维空间中,我们可以找到N个这样的坐标轴,我们取前r个去近似这个空间,这样就从一个N维的空间压缩到r维的空间了,但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
6. 最小二乘问题
想法和 QR 分解的办法类似,主要是利用酉矩阵变换的长度不变性:
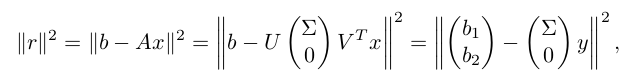
得到最优解是:

机器学习中的矩阵方法04:SVD 分解的更多相关文章
- 机器学习中的矩阵方法(附录A): 病态矩阵与条件数
1. 病态系统 现在有线性系统: Ax = b, 解方程 很容易得到解为: x1 = -100, x2 = -200. 如果在样本采集时存在一个微小的误差,比如,将 A 矩阵的系数 400 改变成 4 ...
- 机器学习(十三)——机器学习中的矩阵方法(3)病态矩阵、协同过滤的ALS算法(1)
http://antkillerfarm.github.io/ 向量的范数(续) 范数可用符号∥x∥λ表示. 经常使用的有: ∥x∥1=|x1|+⋯+|xn| ∥x∥2=x21+⋯+x2n−−−−−− ...
- 机器学习中的矩阵方法03:QR 分解
1. QR 分解的形式 QR 分解是把矩阵分解成一个正交矩阵与一个上三角矩阵的积.QR 分解经常用来解线性最小二乘法问题.QR 分解也是特定特征值算法即QR算法的基础.用图可以将分解形象地表示成: 其 ...
- 《数学之美》第15章 矩阵计算和文本处理中两个分类问题——SVD分解的应用
转载请注明原地址:http://www.cnblogs.com/connorzx/p/4170047.html 提出原因 基于余弦定理对文本和词汇的处理需要迭代的次数太多(具体见14章笔记),为了找到 ...
- 机器学习中的标准化方法(Normalization Methods)
希望这篇随笔能够从一个实用化的角度对ML中的标准化方法进行一个描述.即便是了解了标准化方法的意义,最终的最终还是要:拿来主义,能够在实践中使用. 动机:标准化的意义是什么? 我们为什么要标准化?想象我 ...
- 再谈机器学习中的归一化方法(Normalization Method)
机器学习.数据挖掘工作中,数据前期准备.数据预处理过程.特征提取等几个步骤几乎要花费数据工程师一半的工作时间.同时,数据预处理的效果也直接影响了后续模型能否有效的工作.然而,目前的大部分学术研究主要集 ...
- 投影矩阵、最小二乘法和SVD分解
投影矩阵广泛地应用在数学相关学科的各种证明中,但是由于其概念比较抽象,所以比较难理解.这篇文章主要从最小二乘法的推导导出投影矩阵,并且应用SVD分解,写出常用的几种投影矩阵的形式. 问题的提出 已知有 ...
- CSS3中的矩阵
CSS3中的矩阵 CSS3中的矩阵指的是一个方法,书写为matrix()和matrix3d(),前者是元素2D平面的移动变换(transform),后者则是3D变换.2D变换矩阵为3*3,如下面矩阵示 ...
- 机器学习中的数学-矩阵奇异值分解(SVD)及其应用
转自:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 版权声明: 本文由LeftNotE ...
随机推荐
- 在matlab2015b中配置vlfeat-0.9.18
参考链接: 1.http://cnyubin.com/?p=85 2.http://www.cnblogs.com/woshitianma/p/3872939.html ...
- 04_最长上升子序列问题(LIS)
来源:刘汝佳<算法竞赛入门经典--训练指南> P60 问题6: 问题描述:给定n个整数a1,a2,...,an,按从左到右的顺序选出尽量多的整数,组成一个上升子序列(子序列可以理解为:删除 ...
- python 小程序练习
还有一些小bug 基本有 输入用户名密码 认证成功后显示欢迎信息 输出三次后锁定 # -*- coding:utf-8 -*- account_file=('C:\Users\guigu\Deskto ...
- 构建多模块的Maven项目
在Eclipse下创建一个maven项目,该项目有多个模块组成. 1.创建父项目 File->New->Project->Maven->Maven Project(图一) ...
- myeclipse中运行tomcat报错java.lang.NoClassDefFoundError
有关myeclipse的小问题,在myeclipse中运行tomcat时显示已启动,但是无法访问localhost:8080/,显示404错误.在控制台中发现报错代码如下: java.lang.NoC ...
- NOIP2011提高组 聪明的质监员 -SilverN
题目描述 小T 是一名质量监督员,最近负责检验一批矿产的质量.这批矿产共有 n 个矿石,从 1到n 逐一编号,每个矿石都有自己的重量 wi 以及价值vi .检验矿产的流程是: 1 .给定m 个区间[L ...
- Listview的点击事件
上篇文章总结了如何自定义listview的显示内容,然而listview不能只是提供显示功能,还必须能够点击它显示一些东西: listView.setOnItemClickListener(new O ...
- AC日记——舒适的路线 codevs 1001 (并查集+乱搞)
1001 舒适的路线 2006年 时间限制: 2 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题解 查看运行结果 题目描述 Description Z小镇是 ...
- Daikon Forge GUI 制作图集和字体集
Daikon Forge GUI 制作UI面板 在上次的学习中制作了一个简单的面板,下面来学习制作图集以及字体. 1.DF-GUI 图集(Atlas)制作 操作步骤 选中UI Root根节点,在Sce ...
- 多线程BackgroundWorker
链接:http://www.cnblogs.com/yiyisawa/archive/2008/11/24/1339826.html 周六闲来无事,学习了多线程BackgroundWorker,以此记 ...
