奇怪吸引子---DequanLi
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性、稳定性、吸引性。吸引子是一个数学概念,描写运动的收敛类型。它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它,这样的集合有很复杂的几何结构。由于奇怪吸引子与混沌现象密不可分,深入了解吸引子集合的性质,可以揭示出混沌的规律。
这里会展示利用奇怪吸引子生成的艺术图像。奇怪吸引子通常含有三维或四维的数据,而图像是二维的,因此可以从不同的位面将奇怪吸引子投影到二维图像中。
原图及数学公式取自:
http://chaoticatmospheres.com/125670/1204030/gallery/strange-attractors

这里使用自己定义语法的脚本代码生成混沌图像,相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815。
脚本代码:
[ScriptLines]
u=a*(j-i) + b*i*k
v=c*i + d*j - i*k
w=e*k + i*j - f*i*i
i=i+u*t
j=j+v*t
k=k+w*t
x=i
y=j
z=k [Variables]
a=40.000000
b=0.160000
c=55.000000
d=20.000000
e=1.833000
f=0.650000
i=0.405600
j=1.000000
k=0.000000
t=0.000100
混沌图像:


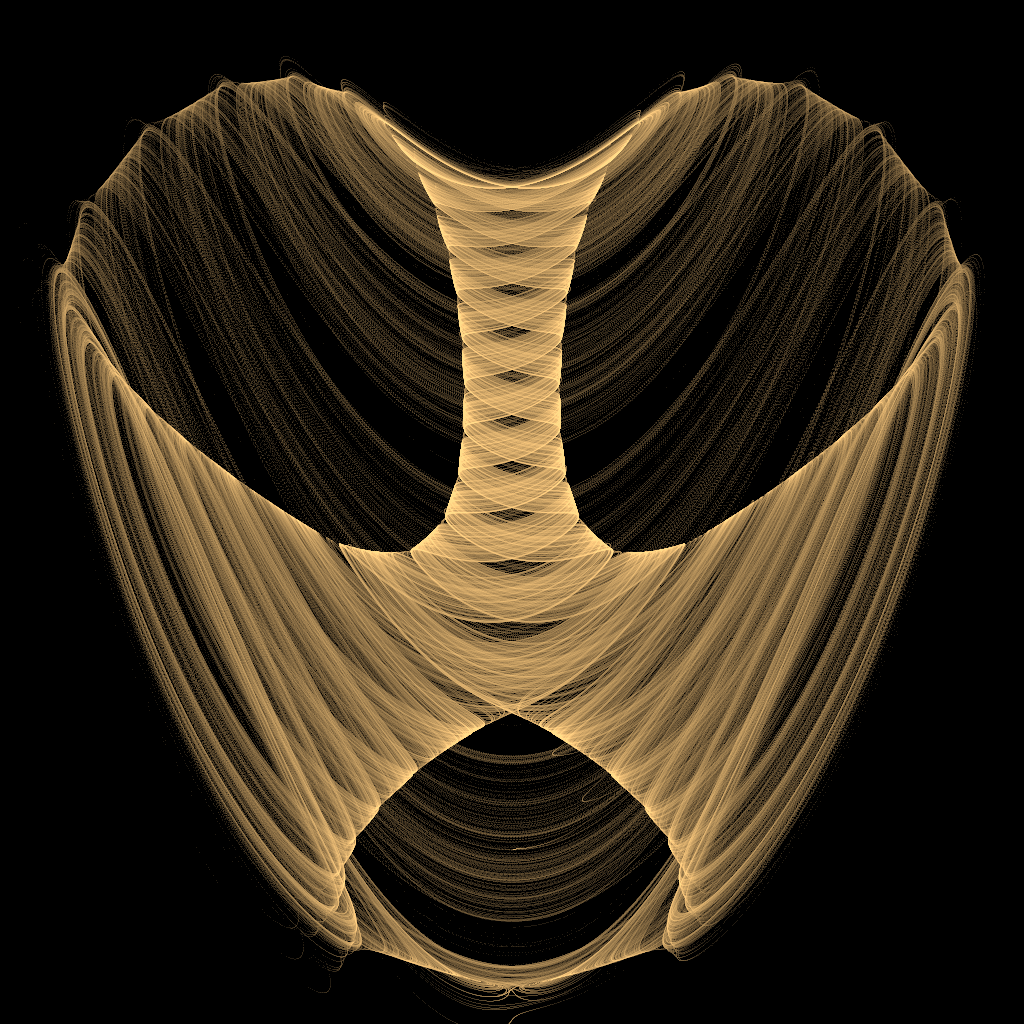

奇怪吸引子---DequanLi的更多相关文章
- 奇怪吸引子---YuWang
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WimolBanlue
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WangSun
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---TreeScrollUnifiedChaoticSystem
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Thomas
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---ShimizuMorioka
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Sakarya
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Russler
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Rucklidge
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
随机推荐
- opesntack 底层共享存储 迁移配置
底层共享存储在迁移配置: 每台compute 节点都需要配置一下 让nova用户可以登陆 usermod -s /bin/bash nova 设置nova 用户密码 echo "nova&q ...
- 「PKUWC2018」猎人杀
「PKUWC2018」猎人杀 解题思路 首先有一个很妙的结论是问题可以转化为已经死掉的猎人继续算在概率里面,每一轮一直开枪直到射死一个之前没死的猎人为止. 证明,设所有猎人的概率之和为 \(W\) , ...
- C# 如何实现邮件发送
调用发送 try { P2BEmail email = new P2BEmail(); email.fromEmail = txtfromEmail.Text; // QQ邮箱 email.fromP ...
- Mac的brew和brew cask区别以及安装brew cask
brew多用于命令行. brew cask主要用于有GUI的软件,例如VLC等等. brew cask是brew的一个子集,也就是一个扩展. 安装brew cask扩展: ruby -e " ...
- LightOJ 1366 - Pair of Touching Circles (统计矩形内外切圆对)
1366 - Pair of Touching Circles PDF (English) Statistics Forum Time Limit: 3 second(s) Memory Limi ...
- LPC43XX TQFP144 IO Pinout
- 78-WS2812-Library (STM32F4)
78-WS2812-Library (STM32F4) //-------------------------------------------------------------- // File ...
- Java学习笔记八(反射)
1.介绍 反射为Java程序在执行时提供了动态的能力.利用反射能够在执行时对程序进行动态的控制.本篇博客着重解说一下Java中的反射. 2.Class类的使用 在Java执行过程中,每一个类被载入后都 ...
- cocos2dx学习之路
http://blog.csdn.net/qq_30501909/article/details/50720227
- 奇妙的 CSS shapes(CSS图形) 【css 图形,绘图,CSS 几何图形)】
http://www.cnblogs.com/coco1s/p/6992177.html <!DOCTYPE html> <html> <head> <met ...
