[机器学习&数据挖掘]朴素贝叶斯数学原理
1、准备:
(1)先验概率:根据以往经验和分析得到的概率,也就是通常的概率,在全概率公式中表现是“由因求果”的果
(2)后验概率:指在得到“结果”的信息后重新修正的概率,通常为条件概率(但条件概率不全是后验概率),在贝叶斯公式中表现为“执果求因”的因
例如:加工一批零件,甲加工60%,乙加工40%,甲有0.1的概率加工出次品,乙有0.15的概率加工出次品,求一个零件是不是次品的概率即为先验概率,已经得知一个零件是次品,求此零件是甲或乙加工的概率是后验概率
(3)全概率公式:设E为随机试验,B1,B2,....Bn为E的互不相容的随机事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,若A是E的事件,则有
P(A) = P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn)
(4)贝叶斯公式:设E为随机试验,B1,B2,....Bn为E的互不相容的随机事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,E的事件A满足P(A)>0,则有
P(Bi|A) = P(Bi)P(A|Bi)/(P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn))
(5)条件概率公式:P(A|B) = P(AB)/P(B)
(6)极大似然估计:极大似然估计在机器学习中想当于经验风险最小化,(离散分布)一般流程:确定似然函数(样本的联合概率分布),这个函数是关于所要估计的参数的函数,然后对其取对数,然后求导,在令导数等于0的情况下,求得参数的值,此值便是参数的极大似然估计
注:经验风险:在度量一个模型的好坏,引入了损失函数,常见的损失函数有:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等,同时风险函数(期望风险)是对损失函数的期望,期望风险是关于联合分布的理论期望,但是理论的联合分布是无法求得的,只能利用样本来估计期望,因此引入经验风险,经验风险就是样本的平均损失,根据大数定理在样本趋于无穷大的时候,这个时候经验风险会无限趋近与期望风险
2、朴素贝叶斯算法
(1)思路:朴素贝叶斯算法的朴素在于对与特征之间看作相互独立的意思例如:输入向量(X1, X2,....,Xn)的各个元素是相互独立的,因此计算概率P(X1=x1,X2=x2,....Xn=xn)=P(X1=x1)P(X2=x2)......P(Xn=xn),其次基于贝叶斯定理,对于给定的训练数据集,首先基于特征条件独立假设学习联合概率分布,然后基于此模型,对于给定的输入向量,利用贝叶斯公式求出后验概率最大的输出分类标签
(2)详细:以判断输入向量x的类别的计算过程来具体说下朴素贝叶斯计算过程
<1>要计算输入向量x的类别,即是求在x的条件下的y的概率,当y取某值最大概率,则此值便为x的分类,则概率为P(Y=ck|X=x)
<2>利用条件概率公式推导贝叶斯公式(此步非必要,本人在记贝叶斯公式时习惯这么记)
由条件概率公式得P(Y=ck|X=x) = P(Y=ck,X=x)/P(X=x) = P(X=x | Y=ck)P(Y=ck)/P(X=x)
由全概率公式可得(替换P(X=x)):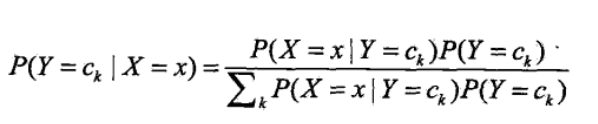
<3>由于朴素贝叶斯的“朴素”,特征向量之间是相互独立的,因此可得如下公式:
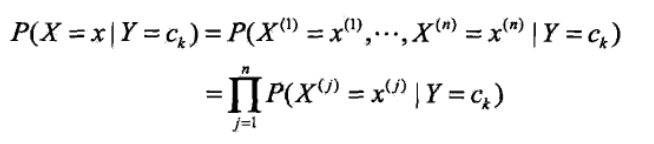
<4>将<3>中的公式带入<2>中的贝叶斯公式可得:
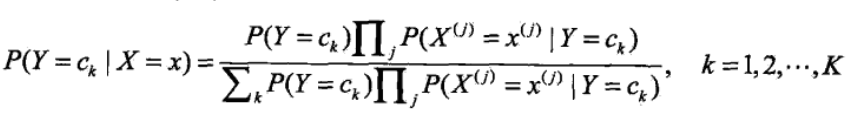
<5>看上式的分母,对于给定的输入向量X,以及Y的所有取值,全部都用了,详细的讲即为无论是计算在向量x条件下的任意一个Y值 ck,k=1,2....K,向量和c1.....ck都用到了,因此影响P(Y=ck|X=x)大小只有分子起作用,因此可得
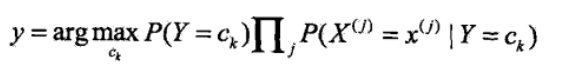
注:argmax指的是取概率最大的ck
<6>其实到<5>朴素贝叶斯的整个过程已经完毕,但是其中的P(Y=ck)和P(X(j)=x(j)|Y=ck)的求解方法并没有说,二者得求解是根据极大似 然估计法来得其概率,即得如下公式:
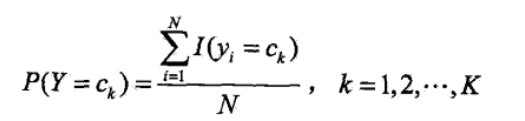
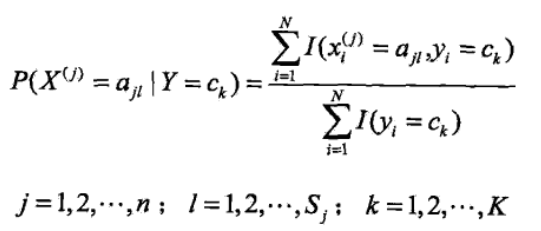
其中的I(..)是指示函数,当然这些概率在实际中可以很块求得,可以看如下得一个题,看完之后就知道这两个概率是怎么求了,公式推导 过程不赘述(具体过程我也不太清楚,不过看作类似二项分布得极大似然求值)
3、题-----一看就把上边得串起来了(直接贴图)
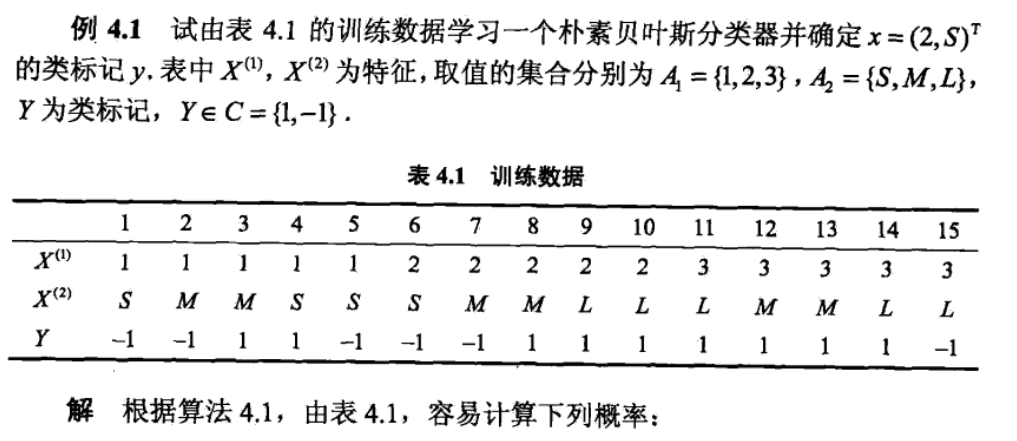

[机器学习&数据挖掘]朴素贝叶斯数学原理的更多相关文章
- Python机器学习算法 — 朴素贝叶斯算法(Naive Bayes)
朴素贝叶斯算法 -- 简介 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法.最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Baye ...
- 100天搞定机器学习|Day15 朴素贝叶斯
Day15,开始学习朴素贝叶斯,先了解一下贝爷,以示敬意. 托马斯·贝叶斯 (Thomas Bayes),英国神学家.数学家.数理统计学家和哲学家,1702年出生于英国伦敦,做过神甫:1742年成为英 ...
- 机器学习之朴素贝叶斯&贝叶斯网络
贝叶斯决决策论 在所有相关概率都理想的情况下,贝叶斯决策论考虑基于这些概率和误判损失来选择最优标记,基本思想如下: (1)已知先验概率和类条件概率密度(似然) (2)利用贝叶斯转化为后验概 ...
- 机器学习:朴素贝叶斯--python
今天介绍机器学习中一种基于概率的常见的分类方法,朴素贝叶斯,之前介绍的KNN, decision tree 等方法是一种 hard decision,因为这些分类器的输出只有0 或者 1,朴素贝叶斯方 ...
- 吴裕雄--天生自然python机器学习:朴素贝叶斯算法
分类器有时会产生错误结果,这时可以要求分类器给出一个最优的类别猜测结果,同 时给出这个猜测的概率估计值. 概率论是许多机器学习算法的基础 在计算 特征值取某个值的概率时涉及了一些概率知识,在那里我们先 ...
- 朴素贝叶斯算法原理及Spark MLlib实例(Scala/Java/Python)
朴素贝叶斯 算法介绍: 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法. 朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,在没有其它可用信息下,我 ...
- 【机器学习实战】第4章 朴素贝叶斯(Naive Bayes)
第4章 基于概率论的分类方法:朴素贝叶斯 朴素贝叶斯 概述 贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类.本章首先介绍贝叶斯分类算法的基础——贝叶斯定理.最后,我们 ...
- Machine Learning in Action(3) 朴素贝叶斯算法
贝叶斯决策一直很有争议,今年是贝叶斯250周年,历经沉浮,今天它的应用又开始逐渐活跃,有兴趣的可以看看斯坦福Brad Efron大师对其的反思,两篇文章:“Bayes'Theorem in the 2 ...
- scikit-learn 朴素贝叶斯类库使用小结
之前在朴素贝叶斯算法原理小结这篇文章中,对朴素贝叶斯分类算法的原理做了一个总结.这里我们就从实战的角度来看朴素贝叶斯类库.重点讲述scikit-learn 朴素贝叶斯类库的使用要点和参数选择. 1. ...
随机推荐
- LintCode——筛子求和
描述:扔n个骰子,向上面的数字之和为 S .给定 Given n,请列出所有可能的 S 值及其相应的概率. 样例:给定n=1,返回 [ [1, 0.17], [2, 0.17], [3, 0.17], ...
- pip virtualenv requirement
原文:https://blog.csdn.net/u011860731/article/details/46561513 pip可以很方便的安装.卸载和管理Python的包.virtualenv则可以 ...
- SCRUM 12.17
今天,我们的用户统计功能终于上线了!! 大家辛苦工作了许久.我们测试的用户统计功能效果模拟如下 还有一些好消息,比如,我们的应用在小米平台收到了崩溃的反馈报告. 这说明我们留下的一些BUG暴露了出来, ...
- 剑指offer:包含min函数的栈
题目描述: 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1)). 解题思路: 相当与在保留原栈的同时,去维护一个最小栈.利用一个辅助栈来完成.对于每个 ...
- Beta版本冲刺(四)
目录 组员情况 组员1(组长):胡绪佩 组员2:胡青元 组员3:庄卉 组员4:家灿 组员:恺琳 组员6:翟丹丹 组员7:何家伟 组员8:政演 组员9:黄鸿杰 组员10:刘一好 组员11:何宇恒 展示组 ...
- week9:个人博客作业
团队作业(5) 以下内容多数是网上的内容,只是做了整合的过程. 要求 在PM 带领下, 每个团队深入分析下面行业的App, 找到行业的Top 5 (从下面的三个备选中,任选一个行业即可) 英语学习/词 ...
- Objective-C runtime 机制
Runtime使用C语言结构体表示对象,用C语言函数表示方法,这些C语言函数和结构体被Runtime封装后,我们就可以在程序中执行创建,检查,修改类和对象和他们的方法 OC的Class其实是一个obj ...
- Alpha冲刺——day6
Alpha冲刺--day6 作业链接 Alpha冲刺随笔集 github地址 团队成员 031602636 许舒玲(队长) 031602237 吴杰婷 031602220 雷博浩 031602634 ...
- Linux命令(十二) 分割文件 split 合并文件 join
一.分割文件 split 命令介绍 当处理文件时,有时需要将文件做分割处理,split 命令用于分割文件,可以分割文本文件,按指定的行数分割,每个分割后的文件都包含相同的行数.split 可以分割非文 ...
- [51CTO]新说MySQL事务隔离级别!
新说MySQL事务隔离级别! 事务隔离级别这个问题,无论是校招还是社招,面试官都爱问!然而目前网上很多文章,说句实在话啊,我看了后我都怀疑作者弄懂没!本文所讲大部分内容,皆有官网作为佐证,因此对本文内 ...
