CS229 7.1应用机器学习中的一些技巧

本文所讲述的是怎么样去在实践中更好的应用机器学习算法，比如如下经验风险最小化问题：

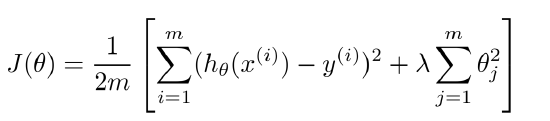
当求解最优的 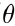 后，发现他的预测误差非常之大，接下来如何处理来使得当前的误差尽可能的小呢？这里给出以下几个选项，下面介绍的是如何在一下这些应对策略中选择正确的方法来助力以上问题。

当模型的variance比较大时，可能存在过拟合，这时可以尝试增多样本或者减少特征或者增大正则参数。

当模型的bias比较大时，可能存在欠拟合，这时可以尝试增加更多的特征或者增加多项特征或减小正则参数。

首先，一般的Mechine Learning问题，我们会把数据分为训练集，交叉验证集，测试集，比例分别为6:2:2.

这样，即可以用一下三哥公式分别计算假设函数在三个集合上的损失：

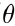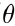接下来，用交叉验证集合找到最优的  ，用该  去到测试机上验证来得到测试误差J_err():

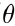bias. variance.

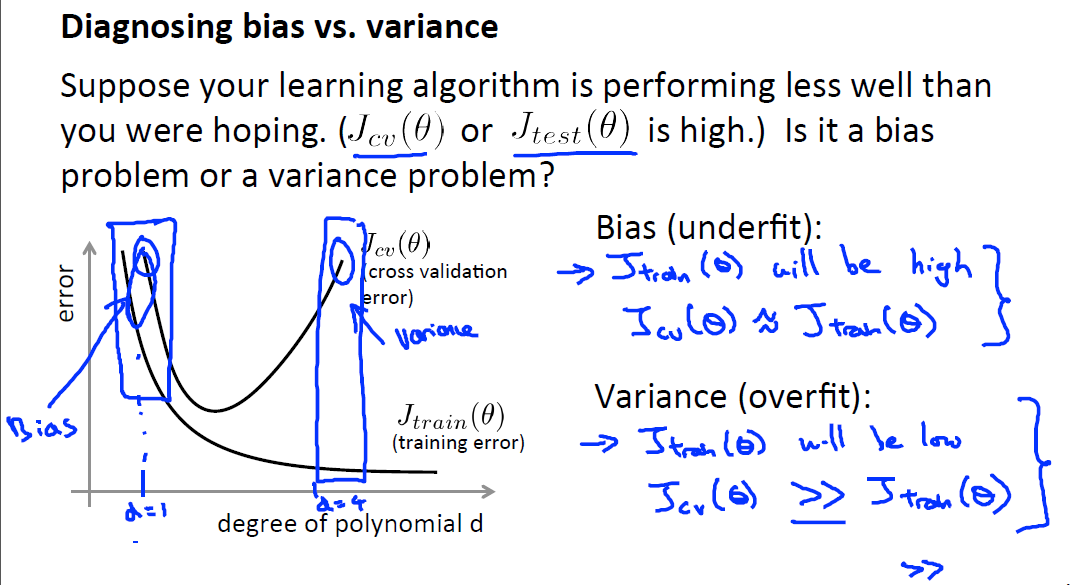
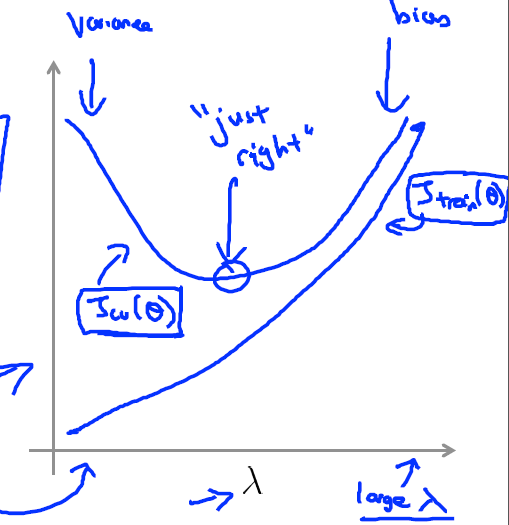
如果目前的算法表现不是很好J_cv或者J_test很高，可以绘制如下关于bias与variance的图来确定是哪里的问题，如果J_train与J_cv均过高，则为bais问题，模型还处于欠拟合的状态，或J_train相对J_cv很低，则为variance问题。

正则化项 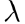 的选取问题，随着  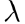的增大，参数  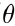的取值会越来越小，模型处于欠拟合状态，偏差bais会越来越大，J_train也会随之增大

在交叉验证集合上，当 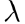 很小时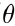，  取值很大，模型可能处于过拟合状态，variance会很大，随着  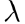增大，J_cv会先减小到最小值，此处的最小值点即为bais与variance比较平衡的地方。当  继续增大，J_cv也会便也会开始增大，最终会导致bais比较大。所以此处J_cv处于最小值的情况下才是最优的  。

增加训练数据

首先注意，随着训练数据的增多，根据6 2 2 的比例，交叉验证集 与 测试集的数据均会增加。

1）当使用一个相对合适的模型时，当数据比较少时，Jtrain会完美拟合训练数据，但此时Jcv会比较大，因为数据少得话模型很难范化到交叉验证集，数据的增加会导致Jtrain增大，Jcv减小，此时增多数据的效果会越来越好。

    

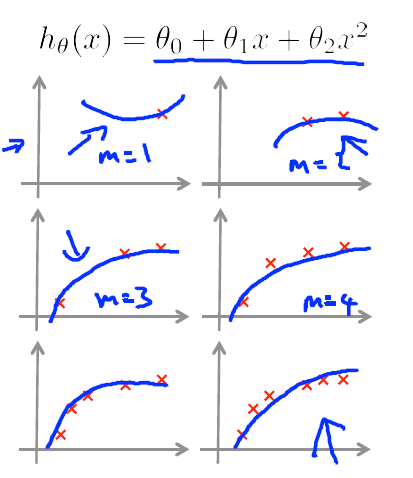
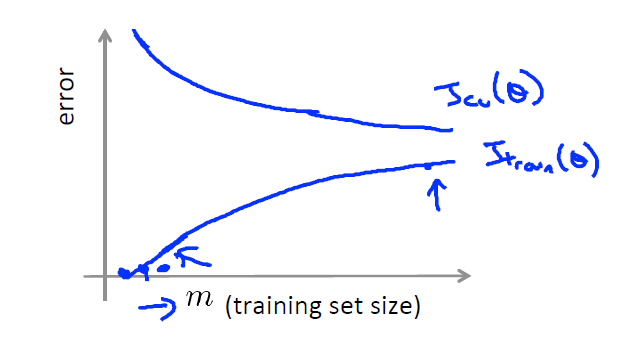
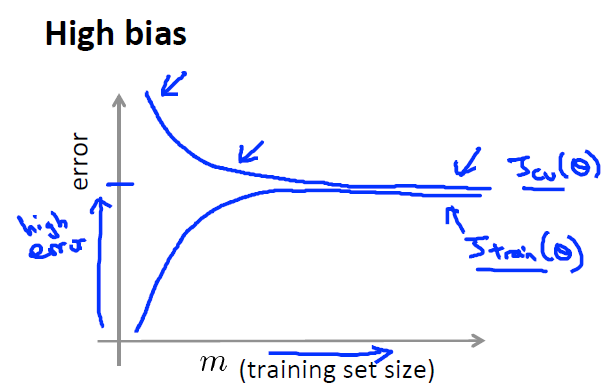
2）当使用一个欠拟合的模型时，会导致J_train非常之大，此时，增大数据量不会有任何效果，因为J_cv不会变的更小，模型无论在测试集还是训练集上都不会有很好的效果。

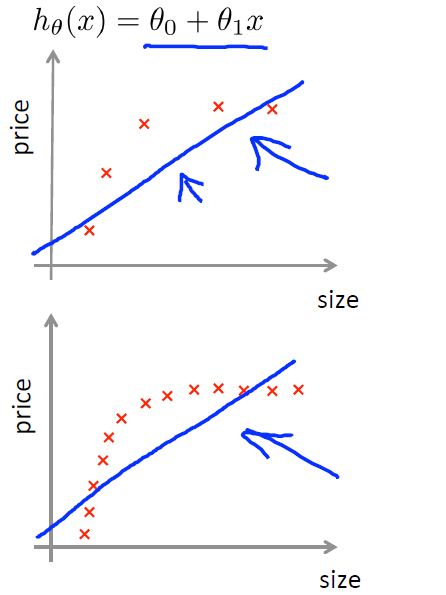
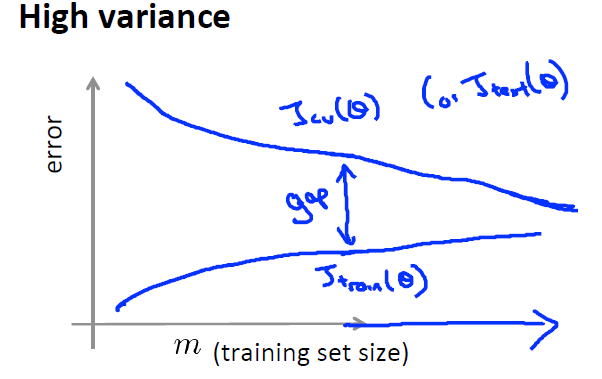
3）当使用一个过拟合的模型时，当数据较少时，J_train与J_cv之间的间隔会比较大，此时增大数据量，效果会有一些提升，J_train与J_cv的间隔会减小，这也就是所谓的增多训练数据来避免过拟合。