Gym - 101492I 区间限制费用流

https://cn.vjudge.net/problem/Gym-101492I

如果用单个点代表每个区间 利用拆点来限制区间的流量的话 点是 n^2/2+m个 边是2*n^2条

但是这样会T

解法1:单纯形

单纯形套板可以过

#include <bits/stdc++.h>
#define N
using namespace std;

typedef unsigned ui;
typedef long double dbl;

const dbl eps = 1e-;

ui n, m, c[]; dbl a[][], x[], z;

int dcmp(dbl d) { return d < -eps ? - : d <= eps ?  : ; }

//    u in, v out
void pivot(ui u, ui v) {
    swap(c[n + u], c[v]);
    //    row u *= 1 / a[u][v]
    dbl k = a[u][v]; a[u][v] = ;
    for (ui j = ; j <= n; ++j) a[u][j] /= k;
    for (ui i = ; i <= m; ++i) {
        if (i == u || !dcmp(a[i][v])) continue;
        k = a[i][v]; a[i][v] = ;
        for (ui j = ; j <= n; ++j)
            a[i][j] -= a[u][j] * k;
    }
}

bool init() {
    for (ui i = ; i <= n; ++i) c[i] = i;
    while () {
        ui u = , v = ;
        for (ui i = ; i <= m; ++i)
            if (dcmp(a[i][]) == - && (!u || dcmp(a[u][] - a[i][]) == )) u = i;
        if (!u) return ;
        for (ui j = ; j <= n && !v; ++j)
            if (dcmp(a[u][j]) == -) v = j;
        if (!v) return ;
        pivot(u, v);
    }
}

int simplex() {
    if (!init()) return ;
    else while () {
        ui u = , v = ;
        for (ui j = ; j <= n; ++j)
            if (dcmp(a[][j]) ==  && (!v || a[][j] > a[][v])) v = j;

        if (!v) {
            z = -a[][];
            for (ui i = ; i <= m; ++i)
                x[c[n + i]] = a[i][];
            return ;
        }

        dbl w = 1e20;
        for (ui i = ; i <= m; ++i)
            if (dcmp(a[i][v]) ==  &&
                dcmp(w - a[i][] / a[i][v]) == ) {
                w = a[i][] / a[i][v];
                u = i;
            }
        if (!u) return ;
        pivot(u, v);
    }
}

int main(void) {
    ios::sync_with_stdio(); cin.tie();
#ifndef ONLINE_JUDGE
    ifstream cin("1.in");
#endif
    ui t;
    cin >> n >> m;
    for (ui j = ; j <= n; ++j) cin >> a[][j];
    for (ui i = ; i <= m; ++i) {
        int l, r; cin >> l >> r;
        for (int j = l; j <= r; ++j)
            a[i][j] = ;
        cin >> a[i][];
    }

    int res = simplex();
    if (res == ) cout << "Infeasible" << endl;
    else if (res == ) cout << "Unbounded" << endl;
    else {
        cout << (long long)z << endl;
    }
    return ;
}

解法2:网络流

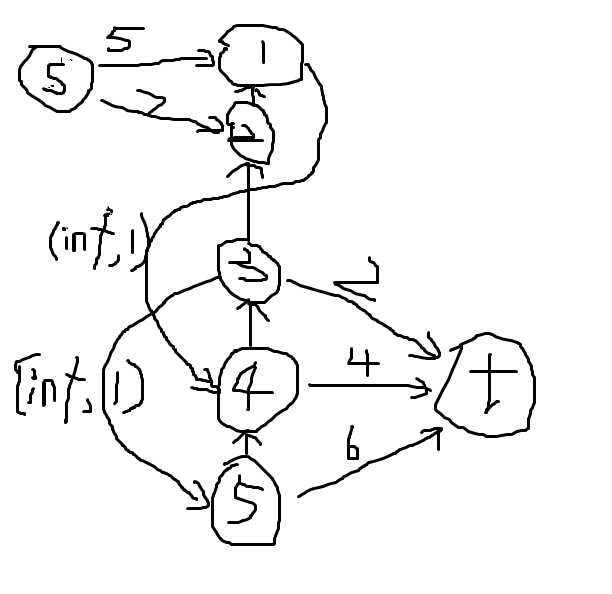
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<string.h>
#include<string>
#include<stdlib.h>
#define inf 0x3f3f3f3f
typedef long long ll;
using namespace std;
const int maxn=;
const int maxm=;
struct node
{
    int t,f,c,next;
}e[maxm*];
int a[maxn];
int head[maxn],dis[maxn],vis[maxn];
int pre[maxn];
int cnt,s,t;
void add(int s,int t,int c,int f)
{
    e[cnt].t=t;
    e[cnt].c=c;
    e[cnt].f=f;
    e[cnt].next=head[s];
    head[s]=cnt++;
    e[cnt].t=s;
    e[cnt].c=;
    e[cnt].f=-f;
    e[cnt].next=head[t];
    head[t]=cnt++;
}
void intt()
{
    cnt=;
    s=;t=;
    memset(head,-,sizeof(head));
}
int spfa()
{
    queue<int >que;
    for(int i=;i<maxn;i++)
    {
        dis[i]=inf;
        vis[i]=;
        pre[i]=-;
    }
    dis[s]=;
    vis[s]=;
    que.push(s);
    while(que.size())
    {
        int u=que.front();
        que.pop();
        vis[u]=;
        for(int i=head[u];i!=-;i=e[i].next)
        {
            int v=e[i].t;
            if(e[i].c>&&dis[u]+e[i].f<dis[v])
            {
                dis[v]=dis[u]+e[i].f;
                pre[v]=i;
                if(vis[v]==)
                {
                    vis[v]=;
                    que.push(v);
                }
            }
        }
    }
    if(pre[t]==-)return ;
    return ;
}
ll mincost()
{
    int flow=;
    ll cost=;
    while(spfa())
    {
      int tf=inf;
      for(int i=pre[t];i!=-;i=pre[e[i^].t])
            tf=min(e[i].c,tf);
      flow+=tf;
      for(int i=pre[t];i!=-;i=pre[e[i^].t])
      {
          e[i].c-=tf;
          e[i^].c+=tf;
          cost+=1ll*e[i].f*tf;
      }
    }
    return cost;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    memset(a,,sizeof(a));
    for(int i=;i<=n;i++)
        scanf("%d",&a[i]);
    intt();
    for(int i=;i<=m;i++)
    {
        int u,v,k;
        scanf("%d%d%d",&u,&v,&k);
        add(u,v+,inf,k);
    }
    for(int i=n+;i>=;i--)
        add(i,i-,inf,);
    for(int i=n+;i>=;i--)
        {
            int temp=a[i]-a[i-];
            if(temp<)
            {
                add(i,t,-temp,);
            }
            else add(s,i,temp,);
        }
    printf("%lld\n",mincost());
}

转载自https://blog.csdn.net/dhydye/article/details/80515359 不懂原理QAQ