Bzoj 1566: [NOI2009]管道取珠(DP)

1566: [NOI2009]管道取珠

Time Limit: 20 Sec Memory Limit: 650 MB

Submit: 1558 Solved: 890

[Submit][Status][Discuss]

Description





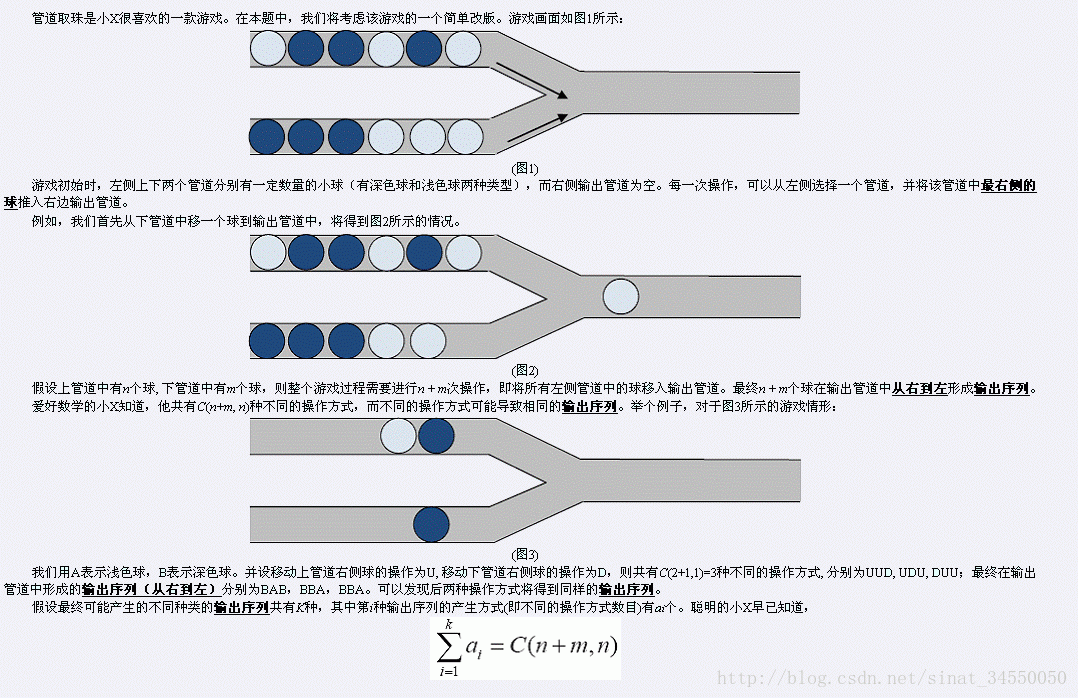
Input

第一行包含两个整数n, m，分别表示上下两个管道中球的数目。 第二行为一个AB字符串，长度为n，表示上管道中从左到右球的类型。其中A表示浅色球，B表示深色球。 第三行为一个AB字符串，长度为m，表示下管道中的情形。

Output

仅包含一行，即为 Sigma(Ai^2) i从1到k 除以1024523的余数。

Sample Input

2 1

AB

B

Sample Output

5

HINT

样例即为文中(图3)。共有两种不同的输出序列形式，序列BAB有1种产生方式，而序列BBA有2种产生方式，因此答案为5。

【大致数据规模】

约30%的数据满足 n, m ≤ 12；

/*
一道DP.
比较妙.
题意相同类型的序列有x个,对答案贡献是x^2。
等价于两个人各自进行操作,得到相同类型序列的方案数.
这个东西是比较好证的。
我们设一个合法序列状态是A,并且现在有x,y两种取法均能得到A
根据乘法原理,那么问题就转化为求A(x,y)二元组的个数.
想象一下现在有两个人正在取数,要求两个人取数相同的方案个数.
令f[i][j][k]表示
people 1 在上面取了i个,下面取了j个
people 2 在上面取了k个，下面取了i+j-k个
people1和people2都取了i+j个数的相同方案的方案个数。
然后枚举上一次取的位置转移即可。。
*/
#include<iostream>
#include<cstdio>
#define mod 1024523
#define MAXN 501
using namespace std;
char a[MAXN],b[MAXN];
int n,m,f[MAXN][MAXN][MAXN];
int main()
{
    scanf("%d %d",&n,&m);
    scanf("%s",a+1);
    scanf("%s",b+1);
    for(int i=1;i<=n/2;i++) swap(a[i],a[n-i+1]);
    for(int i=1;i<=m/2;i++) swap(b[i],b[m-i+1]);
    f[0][0][0]=1;
    for(int i=0;i<=n;i++)
      for(int j=0;j<=m;j++)
        for(int k=0;k<=n;k++)
        {
            int l=i+j-k;int * p=&f[i][j][k];
            if(l<0||l>m) continue;
            if(i&&k&&a[i]==a[k]) *p=(*p+f[i-1][j][k-1])%mod;
            if(i&&l&&a[i]==b[l]) *p=(*p+f[i-1][j][k])%mod;
            if(j&&k&&b[j]==a[k]) *p=(*p+f[i][j-1][k-1])%mod;
            if(j&&l&&b[j]==b[l]) *p=(*p+f[i][j-1][k])%mod;
        }
    printf("%d",f[n][m][n]);
    return 0;
}