中国剩余定理及其拓展 CRT&EXGCD

中国剩余定理，又叫孙子定理。

作为一个梗广为流传。其实它的学名叫中国单身狗定理。

• 中国剩余定理

　　中国剩余定理是来干什么用的呢？

　　其实就是用来解同余方程组的。那么什么又是同余方程组呢。

　　顾名思义就是n个同余方程。

　　形如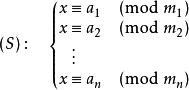

　　如果只有一个方程的话那么是很容易用exgcd来解决。

　　但如果变成n个就需要用到CRT了。

　　下面我们言归正传。

　　首先我们要知道只有满足m_1，m_2，m_n两两互质才能运用CRT。

　　首先，我们令M=Πⁿ_i=1。

　　令Mi=M/m_i，这样我们就可以满足Mi%m_k=0（k！=i）。

　　然后我们在构造n个数，对于每一个数ti满足Mi×ti≡1（mod mi），即ti为Mi在mod mi意义下的乘法逆元（好像是这么叫吧），用exgcd可求。

　　最后再把所有Mi×ti×ai求和再取模就可以了。

　　为什么这样做是正确的呢？因为Mi×ti≡1（mod mi），则Mi×ti×ai≡ai（mod mi）。

　　显然，把所有的数加到一起必定满足方程。（切记不要忘了取模）。

　　一道模板题LOJ10212

　　

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <queue>
 #include <vector>
 using namespace std;
 int m[], a[];
 long long qpow(long long a, long long b) {
     long long ans = ;
     while (b) {
         if (b & )
             ans = ans * a;
         b = b >> ;
         a = a * a;
     }
     return ans;
 }
 long long exgcd(long long a, long long b, long long &x, long long &y) {
     long long t;
     if (!b) {
         x = ;
         y = ;
         return a;
     }
     long long gcd = exgcd(b, a % b, x, y);
     t = x;
     x = y;
     y = t - a / b * y;
     return gcd;
 }
 int main() {
     int n;
     long long M = ;
     scanf("%d", &n);
     for (int i = ; i <= n; i++) {
         scanf("%d%d", &m[i], &a[i]);
         M *= 1ll * m[i];
     }
     long long ans = ;
     for (int i = ; i <= n; i++) {
         long long x, y;
         long long Mi = M / m[i];
         exgcd(Mi, m[i], x, y);
         ans += x * Mi * a[i];
     }
     printf("%lld", (ans % M + M) % M);
 }

CRT

• 拓展中国剩余定理

　　在上面CRT讲解中我们提到所有的m必须两两互质，因为如果不两两互质就可能无解或求错。

　　但是如果毒瘤出题人就让他们不互质呢。

　　那我们就需要把出题人吊起来打一顿用到拓展CRT（实际上他和CRT没有任何关系）

　　首先只考虑有两个方程怎么做

　　x=a₁+k₁×m₁，x=a₂+k₂×m₂ 。可以得到k2×m2-k1×m1=a1-a2。

　　嗯，看起来有点像一个二元一次方程了。

　　我们令 gcd=gcd（m1，m2），c=a1-a2;

　　如果gcd%c！=0则无解

　　否则用exgcd来求出k1×m1+k2×m2=gcd的解k1，再乘上c/gcd就好了。

　　为了避免爆long long 最好取一下模。

　　这样我们就可以反推出x。

　　但注意我们解的方程k1项系数为-1，相当与k1=-k1（所以k1=0？）

　　这样就求出了x。（可以把这个x0转化成最小的非负数解）
　　这个x符合第一个方程，也符合第二个方程。设这个x为x0
　　所以，可以得到通解是：x=x0+k×lcm(m1,m2)　　
　　满足这个条件的x就满足第一第二两个方程。满足第一第二两个方程的所有的解也都是这个方程的解。
　　所以第一第二个方程和这个方程是等价的。
　　将这个方程转化一下，可以得到新的同余方程：x=x0(modlcm(m1,m2))
　　这样，我们成功的把两个方程转化成了一个方程，以此类推。
　　最后留下的这个方程，它的x_0的最小非负数解，就是我们要的最终答案（最后这一段用文本编辑器打的，略显不符，请自动忽略）。

　　例题 poj2891

　　模板题，直接放代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<cstdlib>
 using namespace std;
 #define int long long
 int m[],c[];
 int exgcd(int a,int b,int &x,int &y){
     int t;
     if(!b){
         x=;y=;
         return a;
     }
     int gcd=exgcd(b,a%b,x,y);
     t=x;
     x=y;
     y=t-a/b*y;
     return gcd;
 }
 signed main(){
     int n;
     while(~scanf("%lld",&n)){
         bool ju=;
         for(int i=;i<=n;i++) scanf("%lld%lld",&m[i],&c[i]);
         int m1=m[],c1=c[];
         for(int i=;i<=n;i++){
             int x,y;
             int m2=m[i],c2=c[i];
             int dembele=exgcd(m1,m2,x,y);
             if((c2-c1)%dembele){
                 ju=;
                 printf("-1\n");
                 break;
             }
             x=(c1-c2)/dembele*x%m2;
             c1-=m1*x;
             m1=m1/dembele*m2;
             c1%=m1;
         }
         if(ju)
         printf("%lld\n",(c1%m1+m1)%m1);
     }
 }

EXCRT