The Tower HDU - 6559 （解析几何）

The Tower

The Tower shows a tall tower perched on the top of a rocky mountain. Lightning strikes, setting the building alight, and two people leap from the windows, head first and arms outstretched. It is a scene of chaos and destruction.*

There is a cone tower with base center at (0, 0, 0), base radius r and apex (0, 0, h). At time 0 , a point located at (x0x0, y0y0, z0z0) with velocity (vxvx, vyvy, vzvz). What time will they collide? Here is the cone tower.

Input

The first line contains testcase number TT (TT ≤ 1000), For each testcase the first line contains spaceseparated real numbers rr and hh (1 ≤ rr, hh ≤ 1000) — the base radius and the cone height correspondingly.

For each testcase the second line contains three real numbers x0x0, y0y0, z0z0 (0 ≤ |x0x0|, |y0y0|, z0z0 ≤ 1000). For each testcase the third line contains three real numbers vxvx, vyvy, vzvz (1 ≤ v2xvx2 + v2yvy2 + v2zvz2 ≤ 3 × 106106). It is guaranteed that at time 0 the point is outside the cone and they will always collide.

Output

For each testcase print Case ii : and then print the answer in one line, with absolute or relative error not exceeding 10−610−6

Sample Input

2

1 2

1 1 1

-1.5 -1.5 -0.5

1 1

1 1 1

-1 -1 -1

Sample Output

Case 1: 0.3855293381

Case 2: 0.5857864376

题意：在三维空间中，给你一个底面在XOY面的圆锥，底面圆的圆心在原点。又给定一个动点的初始坐标，以及他的三个坐标轴方向的分速度，请计算出何时动点撞击到圆锥。

思路：我们设撞击的时间为t，那么我们可以根据三个方向的速度获得t时的坐标（x,y,z）又因为碰到了圆锥面

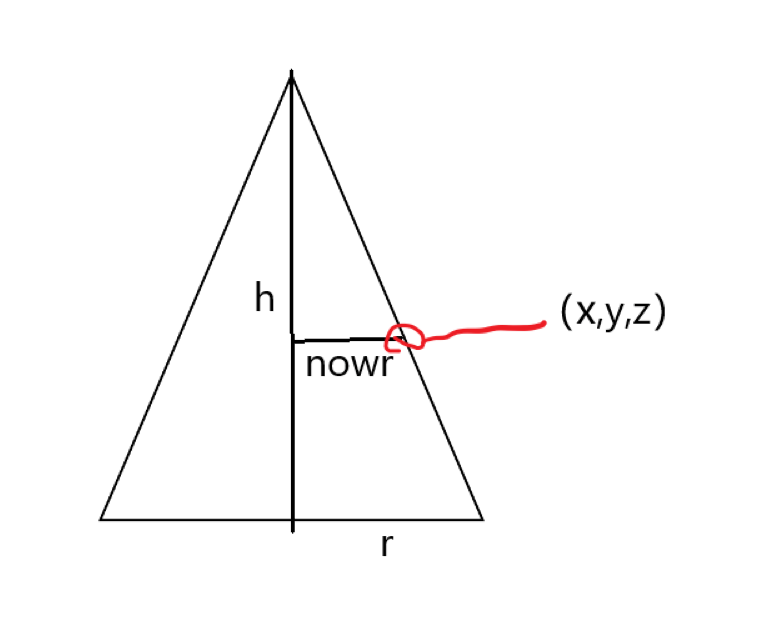
所以根据这个剖视图可以得到图中的nowr，在根据x^2+y2=nowr^2 可以得出一个关于t的一元二次方程，求解判断哪个根符合条件，并且输出小的那一个即可。

具体的方程可以见这个群友的公式：

聚聚的博客连接：https://www.cnblogs.com/Dillonh/p/11196418.html

其实直接输出方程较小的那个根就是答案，具体为什么我还不太清楚。

细节见代码：

#include <iostream>

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <cmath>

#include <queue>

#include <stack>

#include <map>

#include <set>

#include <vector>

#include <iomanip>

#define ALL(x) (x).begin(), (x).end()

#define sz(a) int(a.size())

#define all(a) a.begin(), a.end()

#define rep(i,x,n) for(int i=x;i<n;i++)

#define repd(i,x,n) for(int i=x;i<=n;i++)

#define pii pair<int,int>

#define pll pair<long long ,long long>

#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

#define MS0(X) memset((X), 0, sizeof((X)))

#define MSC0(X) memset((X), '\0', sizeof((X)))

#define pb push_back

#define mp make_pair

#define fi first

#define se second

#define eps 1e-6

#define gg(x) getInt(&x)

#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl

using namespace std;

typedef long long ll;

ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}

ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}

ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2) { ans = ans * a % MOD; } a = a * a % MOD; b /= 2;} return ans;}

inline void getInt(int *p);

const int maxn = 1000010;

const int inf = 0x3f3f3f3f;

/*** TEMPLATE CODE * * STARTS HERE ***/

typedef long double ld;

int main()

{

    //freopen("D:\\code\\text\\input.txt","r",stdin);

    //freopen("D:\\code\\text\\output.txt","w",stdout);

    int t;

    gbtb;

    cin >> t;

    ld x, y, z, r, h, vx, vy, vz;

    repd(cas, 1, t) {

        cin >> r >> h;

        cin >> x >> y >> z;

        cin >> vx >> vy >> vz;

        ld a = (vx * vx + vy * vy - r * r * vz * vz / h / h);

        ld b = (2.0 * x * vx + 2.0 * y * vy - r * r * (2.0 * z * vz - 2.0 * h * vz) / h / h);

        ld c = x * x + y * y - r * r * (h * h + z * z - 2.0 * h * z) / h / h;

        ld g1 = -b - sqrt(b * b - 4.0 * a * c);

        g1 /= 2.0 * a;

        cout << "Case " << cas << ": ";

        cout << fixed << setprecision(7) << g1 << endl;

    }

    return 0;

}

inline void getInt(int *p)

{

    char ch;

    do {

        ch = getchar();

    } while (ch == ' ' || ch == '\n');

    if (ch == '-') {

        *p = -(getchar() - '0');

        while ((ch = getchar()) >= '0' && ch <= '9') {

            *p = *p * 10 - ch + '0';

        }

    } else {

        *p = ch - '0';

        while ((ch = getchar()) >= '0' && ch <= '9') {

            *p = *p * 10 + ch - '0';

        }

    }

}