Sell Pigs 题解

Sell Pigs

双倍经验

题目大意

有 \(n\) 个顾客前来买猪，共有 \(m\) 个猪圈，每个顾客携带着某一些猪圈的钥匙，需要买一定数量的猪。在顾客买完后，我们可以将打开的猪圈中的猪随意移动，移动完毕后所有的猪圈将关闭，直到下一个顾客到来时才能打开其拥有钥匙对应的猪圈。求最多能卖出多少猪。

思路分析

我们注意到顾客是有时间顺序的。因此，我们首先想到可以建立一张分层图，每个点 \((a,b)\) 表示在第 \(a\) 个顾客到来时的第 \(b\) 个猪圈， 那么边的设置就很自然：

• 建立虚拟源点和汇点，源点向每个 \((1,x)\) 点连边，边权为初始的数量。
• 对于每一层再建一个点，将该层所有被打开的点向它连边，同时它向下一层对于的点连边，边权均为 \(+\infty\)，再将其向汇点连边，边权为 \(+\infty\)。

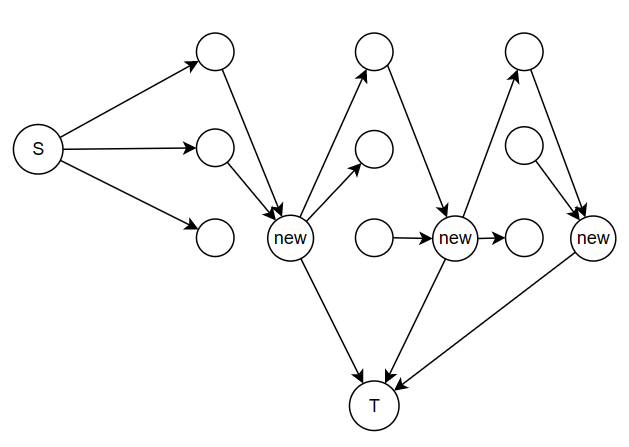
然后跑最大流就可以了。

但是，这样的空间复杂度是 \(O(nm)\) 的，时间复杂度更是高达 \(O(n^3m^3)\)，是比较劣的，如何优化呢？

既然顾客有时间顺序，那么我们不妨从顾客下手，只建立 \(n\) 个代表顾客的点，那么如何连边呢？

• 建立虚拟源点，汇点。
• 每个点向汇点连边，边权是这个顾客对猪的需求量。
• 记录每个猪圈最近一次是被谁打开的，如果是第一次打开，将从源点向这个顾客连的边的边权增加这个猪圈的猪的数量。（如果没有这条边就建立这条边）
• 如果不是第一次打开，将上一次打开这个猪圈的顾客向这个顾客连一条边权是 \(+\infty\) 的边。

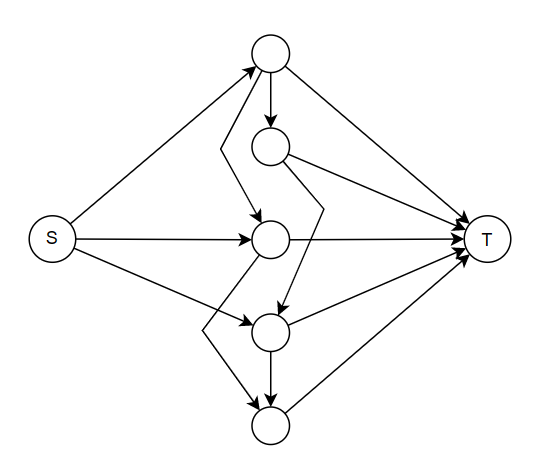
然后跑最大流就可以了。

空间复杂度 \(O(n)\)，时间复杂度 \(O(n^3)\)。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=100100;
#define inf 0x3f3f3f3f

int to[N],nxt[N],head[N],w[N];
int idx=1,n,m,S,T,in1,in2;
int d[N],cur[N];queue <int> q;
int a[N],vis[N];//a 是猪圈中猪的数量，vis 保存上一次打开的人

void add(int u,int v,int c){
    idx++;to[idx]=v;nxt[idx]=head[u];head[u]=idx;w[idx]=c;
    idx++;to[idx]=u;nxt[idx]=head[v];head[v]=idx;w[idx]=0;
}

//dinic模板默写

bool bfs(){
    memset(d,-1,sizeof d);d[S]=0;
    while(!q.empty()) q.pop();
    cur[S]=head[S];q.push(S);
    while(!q.empty()){
        int now=q.front();q.pop();
        for(int i=head[now];i;i=nxt[i]){
            int v=to[i];
            if(~d[v]||!w[i]) continue;
            d[v]=d[now]+1;cur[v]=head[v];
            if(v==T) return 1;q.push(v);
        }
    }
    return 0;
}

int dfs(int s,int lim){
    if(s==T) return lim;
    int flow=0;
    for(int i=cur[s];i&&flow<lim;i=nxt[i]){
        int v=to[i];cur[s]=i;
        if(d[v]!=d[s]+1||!w[i]) continue;
        int t=dfs(v,min(w[i],lim-flow));
        if(!t) d[v]=-1;
        w[i]-=t;w[i^1]+=t;flow+=t;
    }
    return flow;
}

int dinic(){
    int ans=0,flow=0;
    while(bfs()) while(flow=dfs(S,inf)) ans+=flow;
    return ans;
}

//------

int main(){
    scanf("%d%d",&m,&n);
    S=0;T=N-2;//虚拟源汇点
    for(int i=1;i<=m;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++){
        scanf("%d",&in1);
        int sum1=0;
        for(int j=1;j<=in1;j++){
            scanf("%d",&in2);
            if(!vis[in2]){sum1+=a[in2];}//增加边权
            else add(vis[in2],i,inf);//上一个人向这个人连边
            vis[in2]=i;//更新这个猪圈
        }
        if(sum1) add(S,i,sum1);
        scanf("%d",&in1);
        add(i,T,in1);//向汇点连边
    }
    cout<<dinic()<<'\n';
    return 0;
}