云小课｜使用SpringBoot快速构建FunctionGraph HTTP函数

阅识风云是华为云信息大咖，擅长将复杂信息多元化呈现，其出品的一张图(云图说)、深入浅出的博文(云小课)或短视频(云视厅)总有一款能让您快速上手华为云。更多精彩内容请单击此处。

摘要：本篇云小课主要指导使用Springboot应用的用户，快速部署业务到函数工作流FunctionGraph服务。

本文分享自华为云社区《云小课｜使用SpringBoot快速构建FunctionGraph HTTP函数】》，原文作者：阅识风云

本篇云小课将复杂的场景简单化，带你轻轻松松使用SpringBoot快速构建FunctionGraph HTTP函数。

操作流程

此处以http://Spring.io中的IntelliJ IDEA，Maven项目为例，使用HTTP函数的方式部署到FunctionGraph上。

构建代码包

1、打开Springboot项目，在maven插件处单击package，生成jar包。

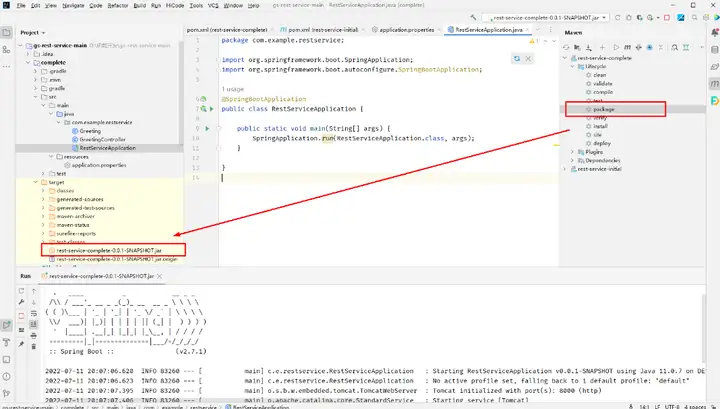
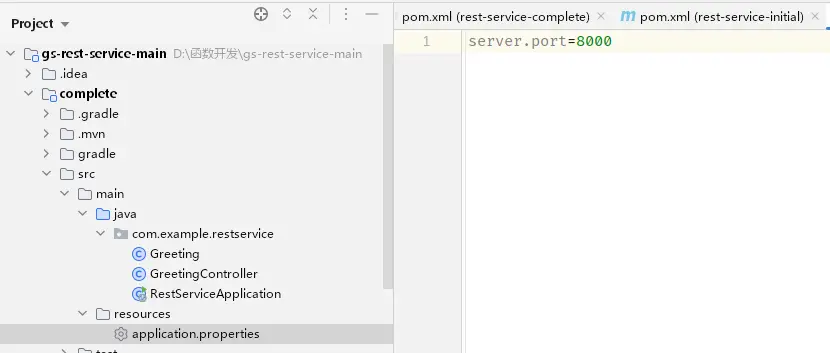
2、配置工程web端口。HTTP函数当前支持8000端口，需配置工程web端口为 8000, 可以参见下图使用application.properties文件来配置，也可以在启动时指定端口号。

3、在jar包同目录创建bootstrap文件并输入启动参数。

/opt/function/runtime/java11/rtsp/jre/bin/java -jar -Dfile.encoding=utf-8 /opt/function/code/rest-service-complete-0.0.1-SNAPSHOT.jar

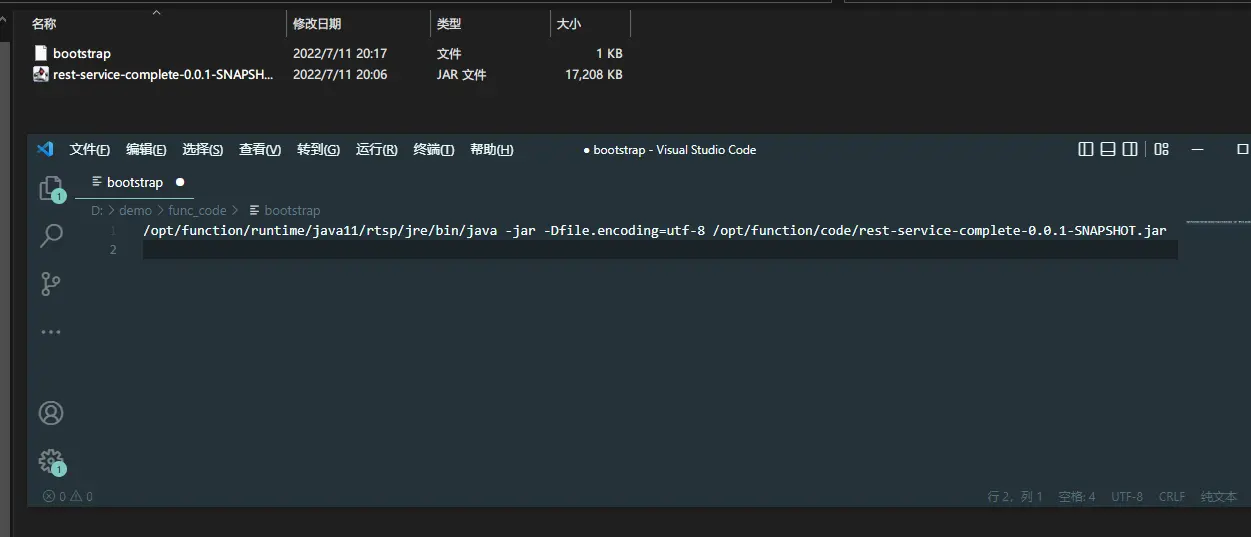
4、选中jar包和bootstrap文件，打包成zip包。（下一步会派上用场哦）

创建HTTP函数并上传代码

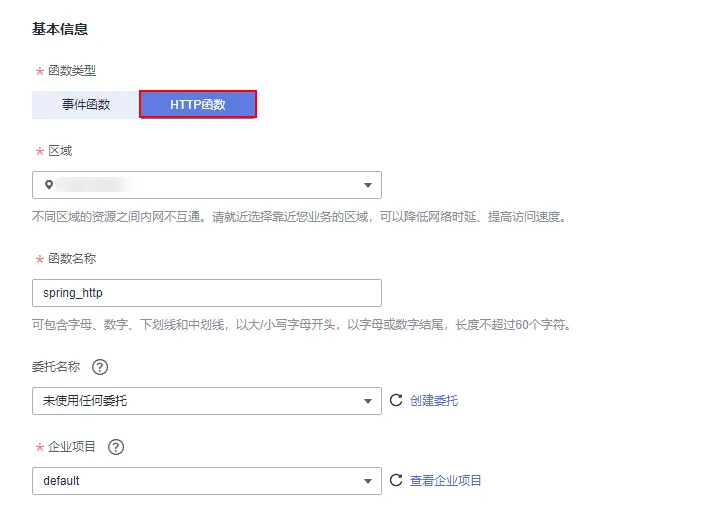
1、在FunctionGraph控制台，创建HTTP函数。

2、上传上一步中由jar包和bootstrap打包的zip包。

验证结果

1、使用函数测试事件验证

在函数详情页，单击“配置测试事件”。
选择事件模板“apig-event-template”，修改测试事件中的path、pathParameters参数，构建一个简单的Get请求。

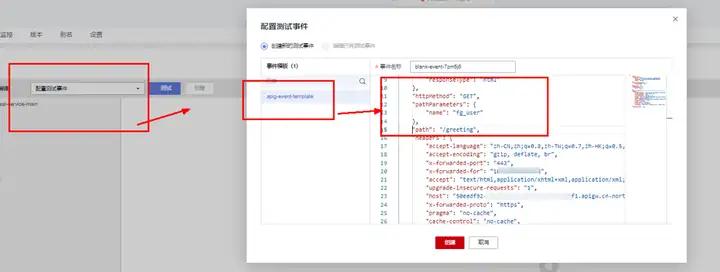
单击“创建”，完成测试事件创建。
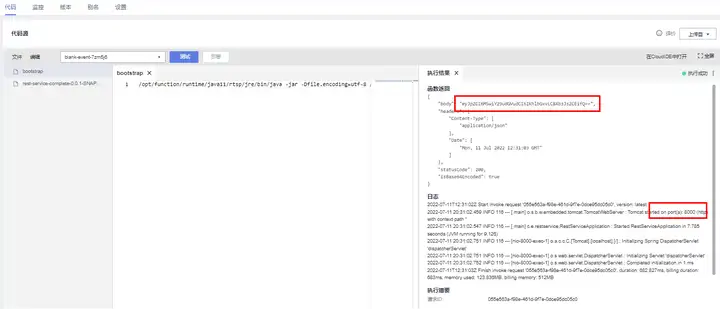
单击“测试”，获取响应。

建议在测试时增加函数内存规格及超时时间，如512MB、5s。

2、配置APIG触发器测试

创建APIG触发器，“安全认证”建议选择“None”，方便调试。

复制生成的调用URL在浏览器进行访问。如图1-6所示，在URL后添加请求参数greeting?name=fg_user，响应如下。

温馨提示：

默认生成的APIG触发器的调用URL为“域名/函数名”，在本案例中即：https://your_host.com/springboot_demo，URL中包含了函数名springboot_demo作为path的第一部分。如果直接Get https://your_host.com/springboot_demo/greeting，springboot接收到的请求地址将包含springboot_demo/greeting两部分。此处需注意：如果用户直接把已有的工程上传，会因为path里多了函数名而无法直接访问自己的服务。因此，请参考以下两种方法注解或去除函数名。

方法一：修改代码中的Mapping地址，例如在GetMapping注解或者类注解上添加默认的path第一部分。

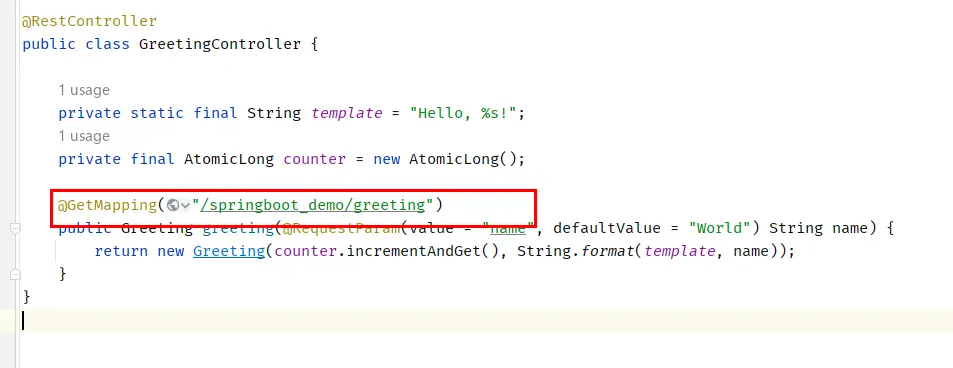
方法二：单击触发器名称，跳转至API网关服务，直接修改path去除函数名。

了解更多FunctionGraph服务信息，戳这里

点击关注，第一时间了解华为云新鲜技术~