神经网络优化篇：将 Batch Norm 拟合进神经网络（Fitting Batch Norm into a neural network）

将 Batch Norm 拟合进神经网络

假设有一个这样的神经网络，之前说过，可以认为每个单元负责计算两件事。第一，它先计算z，然后应用其到激活函数中再计算a，所以可以认为，每个圆圈代表着两步的计算过程。同样的，对于下一层而言，那就是\(z_{1}^{[2]}\)和\(a_{1}^{[2]}\)等。所以如果没有应用Batch归一化，会把输入\(X\)拟合到第一隐藏层，然后首先计算\(z^{[1]}\)，这是由\(w^{[1]}\)和\(b^{[1]}\)两个参数控制的。接着，通常而言，会把\(z^{[1]}\)拟合到激活函数以计算\(a^{[1]}\)。但Batch归一化的做法是将\(z^{[1]}\)值进行Batch归一化，简称BN，此过程将由\({\beta}^{[1]}\)和\(\gamma^{[1]}\)两参数控制，这一操作会给一个新的规范化的\(z^{[1]}\)值（\({\tilde{z}}^{[1]}\)），然后将其输入激活函数中得到\(a^{[1]}\)，即\(a^{[1]} = g^{[1]}({\tilde{z}}^{[ l]})\)。

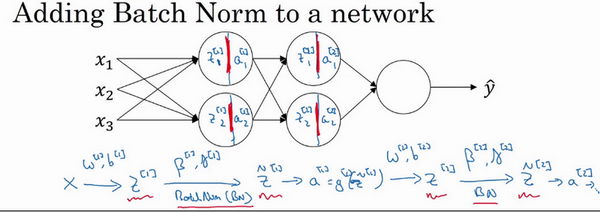
现在，已在第一层进行了计算，此时Batch归一化发生在z的计算和\(a\)之间，接下来，需要应用\(a^{[1]}\)值来计算\(z^{[2]}\)，此过程是由\(w^{[2]}\)和\(b^{[2]}\)控制的。与在第一层所做的类似，会将\(z^{[2]}\)进行Batch归一化，现在简称BN，这是由下一层的Batch归一化参数所管制的，即\({\beta}^{[2]}\)和\(\gamma^{[2]}\)，现在得到\({\tilde{z}}^{[2]}\)，再通过激活函数计算出\(a^{[2]}\)等等。

所以需要强调的是Batch归一化是发生在计算\(z\)和\(a\)之间的。直觉就是，与其应用没有归一化的\(z\)值，不如用归一过的\(\tilde{z}\)，这是第一层（\({\tilde{z}}^{[1]}\)）。第二层同理，与其应用没有规范过的\(z^{[2]}\)值，不如用经过方差和均值归一后的\({\tilde{z}}^{[2]}\)。所以，网络的参数就会是\(w^{[1]}\)，\(b^{[1]}\)，\(w^{[2]}\)和\(b^{[2]}\)等等，将要去掉这些参数。但现在，想象参数\(w^{[1]}\)，\(b^{[1]}\)到\(w^{[l]}\)，\(b^{[l]}\)，将另一些参数加入到此新网络中\({\beta}^{[1]}\)，\({\beta}^{[2]}\)，\(\gamma^{[1]}\)，\(\gamma^{[2]}\)等等。对于应用Batch归一化的每一层而言。需要澄清的是，请注意，这里的这些\(\beta\)（\({\beta}^{[1]}\)，\({\beta}^{[2]}\)等等）和超参数\(\beta\)没有任何关系，下面会解释原因，后者是用于Momentum或计算各个指数的加权平均值。Adam论文的作者，在论文里用\(\beta\)代表超参数。Batch归一化论文的作者，则使用\(\beta\)代表此参数（\({\beta}^{[1]}\)，\({\beta}^{[2]}\)等等），但这是两个完全不同的\(\beta\)。在两种情况下都决定使用\(\beta\)，以便阅读那些原创的论文，但Batch归一化学习参数\({\beta}^{[1]}\)，\({\beta}^{\left\lbrack2 \right\rbrack}\)等等和用于Momentum、Adam、RMSprop算法中的\(\beta\)不同。

所以现在，这是算法的新参数，接下来可以使用想用的任何一种优化算法，比如使用梯度下降法来执行它。

举个例子，对于给定层，会计算\(d{\beta}^{[l]}\)，接着更新参数\(\beta\)为\({\beta}^{[l]} = {\beta}^{[l]} - \alpha d{\beta}^{[l]}\)。也可以使用Adam或RMSprop或Momentum，以更新参数\(\beta\)和\(\gamma\)，并不是只应用梯度下降法。

即使在之前的说明中，已经解释过Batch归一化是怎么操作的，计算均值和方差，减去均值，再除以方差，如果它们使用的是深度学习编程框架，通常不必自己把Batch归一化步骤应用于Batch归一化层。因此，探究框架，可写成一行代码，比如说，在TensorFlow框架中，可以用这个函数（tf.nn.batch_normalization）来实现Batch归一化，稍后讲解，但实践中，不必自己操作所有这些具体的细节，但知道它是如何作用的，可以更好的理解代码的作用。但在深度学习框架中，Batch归一化的过程，经常是类似一行代码的东西。

所以，到目前为止，已经讲了Batch归一化，就像在整个训练站点上训练一样，或就像正在使用Batch梯度下降法。

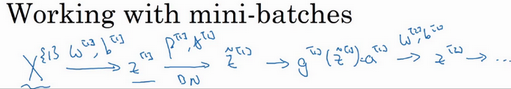
实践中，Batch归一化通常和训练集的mini-batch一起使用。应用Batch归一化的方式就是，用第一个mini-batch(\(X^{\{1\}}\))，然后计算\(z^{[1]}\)，这和上面所做的一样，应用参数\(w^{[1]}\)和\(b^{[1]}\)，使用这个mini-batch(\(X^{\{1\}}\))。接着，继续第二个mini-batch(\(X^{\{2\}}\))，接着Batch归一化会减去均值，除以标准差，由\({\beta}^{[1]}\)和\(\gamma^{[1]}\)重新缩放，这样就得到了\({\tilde{z}}^{[1]}\)，而所有的这些都是在第一个mini-batch的基础上，再应用激活函数得到\(a^{[1]}\)。然后用\(w^{[2]}\)和\(b^{[2]}\)计算\(z^{[2]}\)，等等，所以做的这一切都是为了在第一个mini-batch(\(X^{\{1\}}\))上进行一步梯度下降法。

类似的工作，会在第二个mini-batch（\(X^{\left\{2 \right\}}\)）上计算\(z^{[1]}\)，然后用Batch归一化来计算\({\tilde{z}}^{[1]}\)，所以Batch归一化的此步中，用第二个mini-batch（\(X^{\left\{2 \right\}}\)）中的数据使\({\tilde{z}}^{[1]}\)归一化，这里的Batch归一化步骤也是如此，让来看看在第二个mini-batch（\(X^{\left\{2 \right\}}\)）中的例子，在mini-batch上计算\(z^{[1]}\)的均值和方差，重新缩放的\(\beta\)和\(\gamma\)得到\(z^{[1]}\)，等等。

然后在第三个mini-batch（\(X^{\left\{ 3 \right\}}\)）上同样这样做，继续训练。

现在，想澄清此参数的一个细节。先前说过每层的参数是\(w^{[l]}\)和\(b^{[l]}\)，还有\({\beta}^{[l]}\)和\(\gamma^{[l]}\)，请注意计算\(z\)的方式如下，\(z^{[l]} =w^{[l]}a^{\left\lbrack l - 1 \right\rbrack} +b^{[l]}\)，但Batch归一化做的是，它要看这个mini-batch，先将\(z^{[l]}\)归一化，结果为均值0和标准方差，再由\(\beta\)和\(\gamma\)重缩放，但这意味着，无论\(b^{[l]}\)的值是多少，都是要被减去的，因为在Batch归一化的过程中，要计算\(z^{[l]}\)的均值，再减去平均值，在此例中的mini-batch中增加任何常数，数值都不会改变，因为加上的任何常数都将会被均值减去所抵消。

所以，如果在使用Batch归一化，其实可以消除这个参数（\(b^{[l]}\)），或者也可以，暂时把它设置为0，那么，参数变成\(z^{[l]} = w^{[l]}a^{\left\lbrack l - 1 \right\rbrack}\)，然后计算归一化的\(z^{[l]}\)，\({\tilde{z}}^{[l]} = \gamma^{[l]}z^{[l]} + {\beta}^{[l]}\)，最后会用参数\({\beta}^{[l]}\)，以便决定\({\tilde{z}}^{[l]}\)的取值，这就是原因。

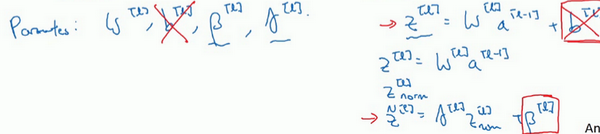
所以总结一下，因为Batch归一化超过了此层\(z^{[l]}\)的均值，\(b^{[l]}\)这个参数没有意义，所以，必须去掉它，由\({\beta}^{[l]}\)代替，这是个控制参数，会影响转移或偏置条件。

最后，请记住\(z^{[l]}\)的维数，因为在这个例子中，维数会是\((n^{[l]},1)\)，\(b^{[l]}\)的尺寸为\((n^{[l]},1)\)，如果是l层隐藏单元的数量，那\({\beta}^{[l]}\)和\(\gamma^{[l]}\)的维度也是\((n^{[l]},1)\)，因为这是隐藏层的数量，有\(n^{[l]}\)隐藏单元，所以\({\beta}^{[l]}\)和\(\gamma^{[l]}\)用来将每个隐藏层的均值和方差缩放为网络想要的值。

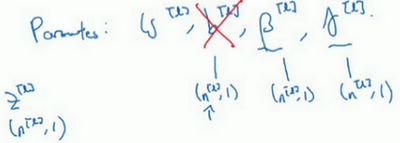
让总结一下关于如何用Batch归一化来应用梯度下降法，假设在使用mini-batch梯度下降法，运行\(t=1\)到batch数量的for循环，会在mini-batch \(X^{\left\{ t\right\}}\)上应用正向prop，每个隐藏层都应用正向prop，用Batch归一化代替\(z^{[l]}\)为\({\tilde{z}}^{[l]}\)。接下来，它确保在这个mini-batch中，\(z\)值有归一化的均值和方差，归一化均值和方差后是\({\tilde{z}}^{[l]}\)，然后，用反向prop计算\(dw^{[l]}\)和\(db^{[l]}\)，及所有l层所有的参数，\(d{\beta}^{[l]}\)和\(d\gamma^{[l]}\)。尽管严格来说，因为要去掉\(b\)，这部分其实已经去掉了。最后，更新这些参数：\(w^{[l]} = w^{[l]} -\text{αd}w^{[l]}\)，和以前一样，\({\beta}^{[l]} = {\beta}^{[l]} - {αd}{\beta}^{[l]}\)，对于\(\gamma\)也是如此\(\gamma^{[l]} = \gamma^{[l]} -{αd}\gamma^{[l]}\)。

如果已将梯度计算如下，就可以使用梯度下降法了，这就是写到这里的，但也适用于有Momentum、RMSprop、Adam的梯度下降法。与其使用梯度下降法更新mini-batch，可以使用这些其它算法来更新，也可以应用其它的一些优化算法来更新由Batch归一化添加到算法中的\(\beta\) 和\(\gamma\) 参数。

能学会如何从头开始应用Batch归一化，如果想的话。如果使用深度学习编程框架之一，之后会谈。如果希望可以直接调用别人的编程框架，这会使Batch归一化的使用变得很容易。