机器学习理论基础学习13--- 隐马尔科夫模型 (HMM)

隐含马尔可夫模型并不是俄罗斯数学家马尔可夫发明的，而是美国数学家鲍姆提出的，隐含马尔可夫模型的训练方法（鲍姆-韦尔奇算法）也是以他名字命名的。隐含马尔可夫模型一直被认为是解决大多数自然语言处理问题最为快速、有效的方法。

现实世界中有一类问题具有明显的时序性，比如路口红绿灯、连续几天的天气变化，我们说话的上下文，HMM的基础假设就是，一个连续的时间序列事件，它的状态受且仅受它前面的N个事件决定，对应的时间序列可以成为N阶马尔可夫链。

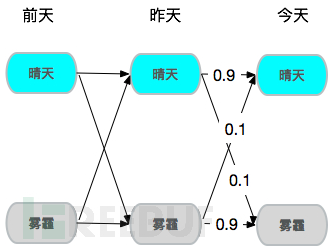
假设今天是否有雾霾只由前天和昨天决定，于是就构成了一个2阶马尔可夫链，若昨天和前天都是晴天，那么今天是晴天概率就是90%。

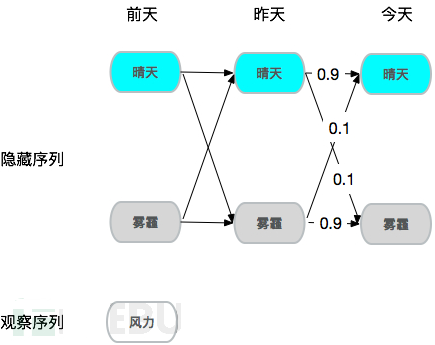
稍微再复杂点，假设你想知道2000公里外一个城市的雾霾情况，但是你没法直接去当地看到空气情况，手头只有当地风力情况，也就是说空气状态是隐藏的，风力情况是可观察的，需要观察序列推测隐藏序列，由于风力确实对雾霾情况有较大影响，甚至可以假设风力大的情况下90%概率是晴天，所以通过样本学习，确实可以达到从观察序列推测隐藏序列的效果，这就是隐式马尔可夫。

一个模型，两个假设，三个问题

1.一个模型

2.两个假设

3.三个问题

• 问题一 evaluation ---->前向算法和后向算法
  前提：假设发射概率矩阵、转移矩阵、初始概率已知
  目的：求在已知观测数据X下的某个隐状态Z的概率

前向算法：

计算给定了观测数据后，这些数据跟目前HMM的参数的相似程度。或者说来计算观测数据在这些参数下的似然。前向算法要求\[ p(Z_k,X_{1:k}) \]，这里要明确的是状态的序号是跟观测序列的结尾是同步的，这个这个过程可以叫做filtering，就是在这 个序列的后验分布，我们可以用D-separation来继续化解。

这个式子可以解释成为对于每个Z k 来说先计算它的发散概率和转换概率乘以上一个Zk的对应的式子，然后把它们全部加起来。这样就构成了一个递归的式子。动态规划的最基本的一个思想就是要用递归的方法来解决问题。

后向算法：

后向算法的意义没有前向算法的那么强，但是是构成F/B算法的一部分。我们要来计算这一部分：

• 问题二 learning 参数怎么求？
  分为两种：1）监督学习方法：训练数据包括观测序列和对应的状态序列 --> 极大似然估计
  2）Baum-Welch算法 --> 它是EM算法在HMM中的具体实现，由Baum和Welch提出

• 问题三 decoding
  维特比算法 ：已知模型和观测序列，求对给定观测序列条件概率P(I|O)最大的状态序列I=(i1,i2,...,iT) [维特比算法应用动态规划高效的求解最优路径，即概率最大的状态序列
  再细分，可得到：
  1）预测 p(it+1|O1,O2,...,Ot)
  2）滤波 p(it|O1,O2,...,Ot)

总结

• HMM是一个概率模型，对于观测量分布和状态分布均有概率解释
• HMM是一个时序模型，对状态序列做了自相关一阶的建模和假设,即马尔科夫假设
• HMM是一个非监督学习模型，可以看成是一个聚类模型，隐状态可以给我们看待问题的全新角度
• HMM是一个预测模型，对未来观测值的预测本质上就是隐状态所代表的概率分布的加权平均
• HMM是一个贝叶斯模型，可以对观测分布预设初始信念参数
• HMM需要预设隐状态数量，这个有一定的人为性
• HMM需要预测观测分布，比如高斯分布、高斯混合分布
• HMM对状态序列平滑的效果似乎要超过对状态预测的效果，最著名的就是Viterbi算法

参考

机器不学习:HMM模型解析

HMM模型和Viterbi算法

HMM 理论基础及金融市场的应用（一）