Frog and Portal(思维好题)

Frog and Portal

https://hihocoder.com/problemset/problem/1873

时间限制:1000ms

单点时限:1000ms

内存限制:512MB

描述

A small frog wants to get to the other side of a river. The frog is initially located at one bank of the river (position 0) and wants to get to the other bank (position 200). Luckily, there are 199 leaves (from position 1 to position 199) on the river, and the frog can jump between the leaves. When at position p, the frog can jump to position p+1 or position p+2.

How many different ways can the small frog get to the bank at position 200? This is a classical problem. The solution is the 201st number of Fibonacci sequence. The Fibonacci sequence is constructed as follows: F1=F2=1;Fn=Fn-1+Fn-2.

Now you can build some portals on the leaves. For each leaf, you can choose whether to build a portal on it. And you should set a destination for each portal. When the frog gets to a leaf with a portal, it will be teleported to the corresponding destination immediately. If there is a portal at the destination, the frog will be teleported again immediately. If some portal destinations form a cycle, the frog will be permanently trapped inside. Note that You cannot build two portals on the same leaf.

Can you build the portals such that the number of different ways that the small frog gets to position 200 from position 0 is M?

输入

There are no more than 100 test cases.

Each test case consists of an integer M, indicating the number of ways that the small frog gets to position 200 from position 0. (0 ≤ M < 232)

输出

For each test case:

The first line contains a number K, indicating the number of portals.

Then K lines follow. Each line has two numbers ai and bi, indicating that you place a portal at position ai and it teleports the frog to position bi.

You should guarantee that 1 ≤ K, ai, bi ≤ 199, and ai ≠ aj if i ≠ j. If there are multiple solutions, any one of them is acceptable.

样例输入

0
1
5

样例输出

2
1 1
2 1
2
1 199
2 2
2
4 199
5 5

一句话题意：给定一个数，用x个斐波那契数列中的数去凑成这个x

用类似下面图的方法去构造

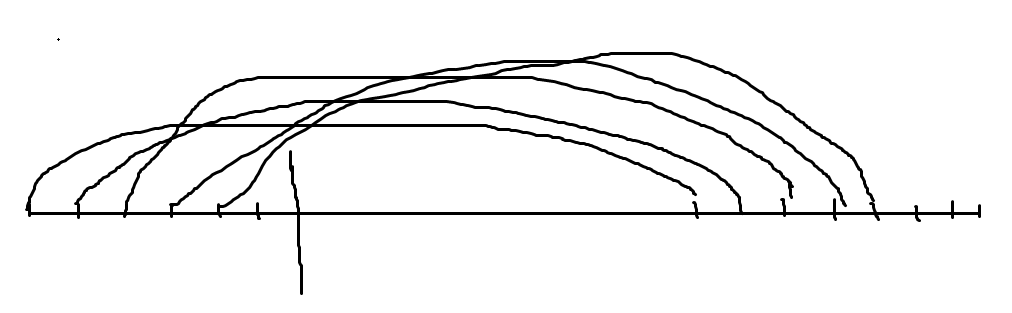
 #include<iostream>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<cmath>
 #include<cstdio>
 #include<map>
 #include<vector>
 #include<queue>
 #include<set>
 using namespace std;
 typedef long long ll;
 ll a[];
 ll m;
 int ans[][];
 void AC(){
     int co=;
     int k=;
     while(m){
         int p=upper_bound(a,a+,m)-a;
         p--;
         ans[co][]=k,ans[co++][]=-p;
         m-=a[p];
         k+=;
     }
     cout<<co+<<endl;
     for(int i=;i<co;i++){
         cout<<ans[i][]<<" "<<ans[i][]<<endl;
     }
     cout<<ans[co-][]+<<" "<<ans[co-][]+<<endl;
 }

 int main()
 {
     std::ios::sync_with_stdio(false);
     std::cin.tie();
     std::cout.tie();
     a[]=;a[]=;a[]=;
     for(int i=;i<=;i++){
         a[i]=a[i-]+a[i-];
     }
     while(cin>>m){
         bool flag=false;
         if(m==){
             cout<<<<endl;
             cout<<"1 1"<<endl;
             cout<<"2 1"<<endl;
             continue;
         }
         int ans1,ans2;
         AC();
     }
     return ;
 }