BZOJ 1009: [HNOI2008]GT考试（kmp+dp+矩阵优化）

http://www.lydsy.com/JudgeOnline/problem.php?id=1009

题意：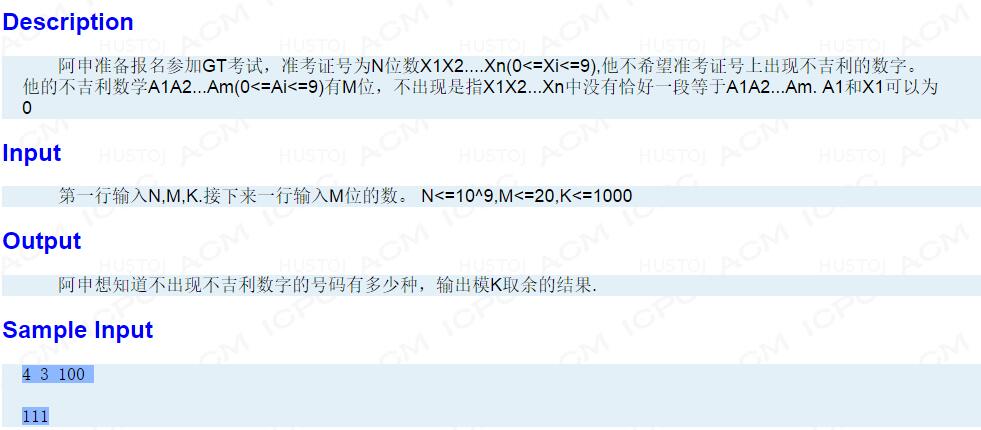

思路：
真的是好题啊！

对于这种题目，很有可能就是dp，$f[i][j]$表示分析到第 i 位时匹配了不吉利数字的前 j 位，那么对于第i+1位来说，它有3种情况：

①加入第i +1位后，和不吉利数字不匹配了，也就是变成了$f[i+1][0]$。

②这种情况还是不匹配，但是它不回到0，这个就是kmp，这样一说是不是想明白了。

③继续匹配，也就是$f[i+1][j+1]$。

这个计算的话可以用矩阵来加速：

$a[i][j]$表示从匹配i个数变到匹配j个数的方法数。$a[i][j]$的初始化就靠kmp来完成了。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n, m, mod;
 char s[];
 int nxt[maxn];

 struct Matrix
 {
     int mat[][];
     Matrix operator *(Matrix a)
     {
         Matrix c;
         for(int i=;i<m;i++)
         {
             for(int j=;j<m;j++)
             {
                 c.mat[i][j]=;
                 for(int k=;k<m;k++)
                     c.mat[i][j]=(c.mat[i][j]+mat[i][k]*a.mat[k][j])%mod;
             }
         }
         return c;
     }
 }base,a;

 void qpow(int n)
 {
     for(int i=;i<m;i++)
     {
         a.mat[i][i]=;
         for(int j=i+;j<m;j++)
             a.mat[i][j]=a.mat[j][i]=;
     }

     while(n)
     {
         if(n&)  a=a*base;
         base=base*base;
         n>>=;
     }
 }

 void get_next()
 {
     int i = -, j = ;
     nxt[] = -;
     while (j < m)
     {
         if (i == - || s[i] == s[j])
             nxt[++j] = ++i;
         else
             i = nxt[i];
     }
 }

 void kmp()
 {
     memset(base.mat,,sizeof(base.mat));

     for(int i=;i<m;i++)
     {
         for(char j='';j<='';j++)
         {
             int k=i;
             while(k && s[k]!=j)  k=nxt[k];
             if(s[k]==j)  k++;
             if(k!=m)   base.mat[i][k]++;
         }
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d%d%s",&n,&m,&mod,s))
     {
         get_next();
         kmp();
         qpow(n);
         int ans=;
         for(int i=;i<m;i++)
             ans=(ans+a.mat[][i])%mod;
         printf("%d\n",ans);
     }
     return ;
 }