[Algorithm] Reservoir Sampling

Given a stream of elements too large to store in memory, pick a random element from the stream with uniform probability.

To solve the problem which n size is unknown, Reservior Sampling is a perfect algorithm to use:

Reservoir sampling algorithm can be used for randomly choosing a sample from a stream of n items, where n is unknow.

Here we still need to prove that

Consider the (i)th item, with its compatibility probability of 1/i. The probability I will be choose the i at the time n > i can be demonstrated by a simple formula

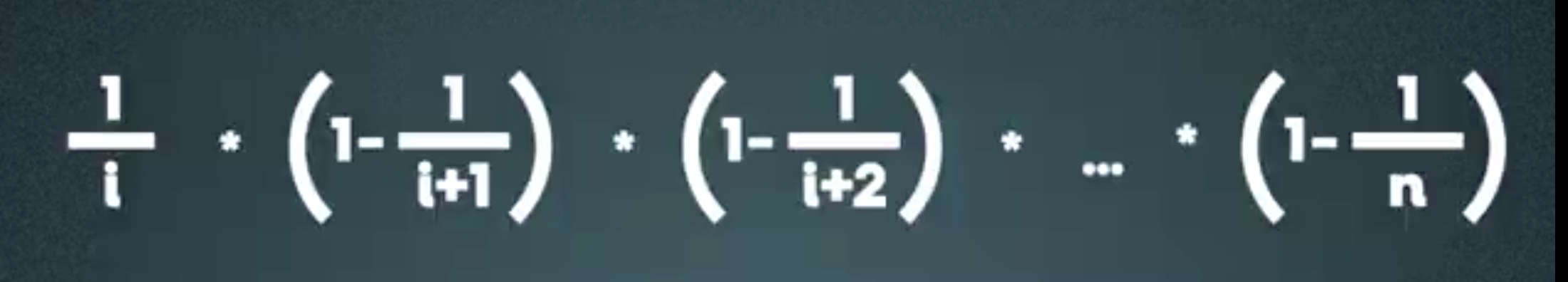
i/i: Probability the ith item will be selected;

(1 - i/i+1): Probability the i+1th item will NOT be selected;

(1 - i/i+2): Probability the i+2th item will NOT be selected;

(1 - 1 / n): Probability the nth item will NOT be selected;

In the end, the probability of ith item will be selected at given n, which n > i is 1/n.

Let’s attempt to solve using loop invariants. On the ith iteration of our loop to pick a random element, let’s assume we already picked an element uniformly from [0, i - 1]. In order to maintain the loop invariant, we would need to pick the ith element as the new random element at 1 / (i + 1) chance. For the base case where i = 0, let’s say the random element is the first one.

function Reservoir_Sampling (ary) {
  let selected;
  const size = ary.length;

  for (let i = 0; i < size; i++) {
    if (Math.floor(Math.random() * size) === 1) {
      selected = ary[i];
      break;
    }
  }

  return selected;
}