图论最短路——spfa

今天开始图论的最短路的最后复习，今天自己手打spfa虽然看了一眼书，但是也算是自己打出来的，毕竟很久没打了，而且还是一遍a代码下来15min左右就搞完了，成就感++。所以呢来篇博客记录一下。

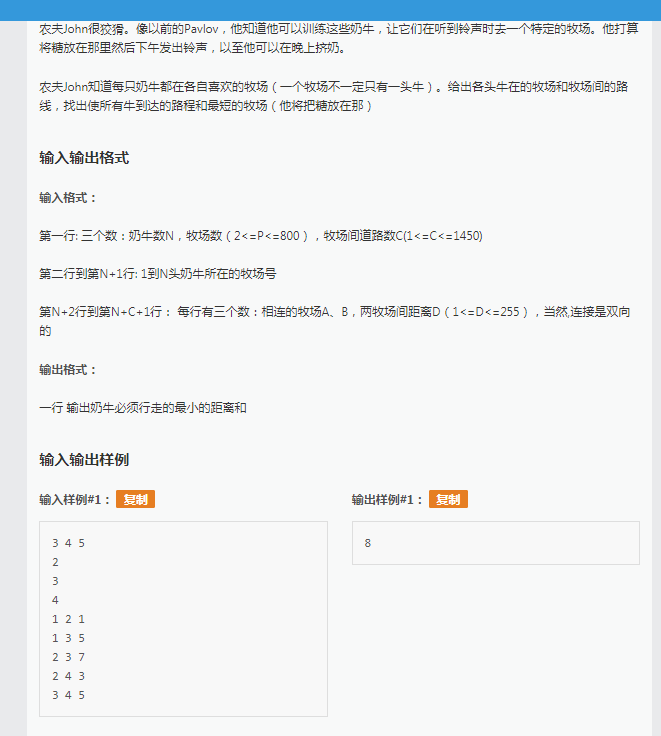
香甜的黄油，当年做的时候吃了不少苦头现在完全会打了，下面是当时我的代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<cmath>
#include<ctime>
#include<iostream>
#include<string>
using namespace std;
const int maxn=,inf=;
int n,p,c,a,b,d,t,dist[maxn],s1[maxn],inq[maxn];
vector<int>g[maxn],w[maxn];

void spfa(int s)
{
    queue<int>a;//一个队列a
    for(int i=;i<=p;i++)//循环4个牧场都附极大值
    dist[i]=inf;
    memset(inq,,sizeof(inq));//清空inp

    dist[s]=;//把到当前的牧场距离设为0，毕竟是自己到自己
    a.push(s);//进队
    inq[s]=;//使其为1

    while(!a.empty())//如果队列不为空
    {
        int i=a.front();//返回队首元素
        a.pop();//弹出队首
        inq[i]=;//使其为0
        for(int k=;k<g[i].size();k++)//当前的牧场和其余的牧场相连
        {
            int j=g[i][k];//取i到j的牧场号询问其距离
            if(dist[i]+w[i][k]<dist[j])//如果当前距离和i到k的距离小于j松弛操作
            {
                dist[j]=dist[i]+w[i][k];//松弛
                if(inq[j]!=) continue;//询问是否在队列之中
                inq[j]=;//不在的话再次标记
                a.push(j);//使当前的点进队好像bfs但不是bfs多次进队
            }
        }
    }
}

int main()
{
    //freopen("1.in","r",stdin);
    scanf("%d%d%d",&n,&p,&c);//n为奶牛所在的牧场号，p为4个牧场，c为5个牧场的关系
    memset(s1,,sizeof(s1));//s1存的是奶牛的牧场位置；
    for(int i=;i<=n;i++)
    {
        scanf("%d",&t);//牛
        s1[t]++;//牧场
    }
    for(int i=;i<=c;i++)
    {
        scanf("%d%d%d",&a,&b,&d);//a与b之间的距离为d
        g[a].push_back(b);//扩边
        g[b].push_back(a);
        w[a].push_back(d);//二次扩边
        w[b].push_back(d);
    }
    int ans=inf;//附最大值
    for(int i=;i<=p;i++)//枚举每一个牧场为起点
    {
        spfa(i);//当黄油放在第i个牧场时来一个一个判断；跑距离
        int sum=;
        for(int j=;j<=p;j++)
        {
            if(!s1[j]) continue;
            sum+=dist[j]*s1[j]; //计算奶牛到牧场的距离和
        }
        ans=min(sum,ans); //取最小值
    }
    printf("%d",ans);
    return ;
}

注释很多很多，主要因为当时的不理解。

下面是本人今天的代码！！！

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<stack>
#include<ctime>
#include<vector>
#include<queue>
#include<map>
#define inf 10000000
using namespace std;
const int maxn=;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int b[maxn],ver[maxn],lin[maxn],nex[maxn],len=,e[maxn],minn=inf,dis[maxn],q[maxn];
bool vis[maxn];
void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
int n,m,k,h,t;
void spfa(int x)
{
    memset(vis,,sizeof(vis));
    memset(dis,,sizeof(dis));
    memset(q,,sizeof(q));
    dis[x]=;vis[x]=;q[]=x;
    h=,t=;
    while(h<=t)
    {
        int tn=q[++h];vis[tn]=;
        for(int i=lin[tn];i;i=nex[i])
        {
            int tmp=ver[i];
            if(dis[tn]+e[i]<dis[tmp])
            {
                dis[tmp]=dis[tn]+e[i];
                if(vis[tmp]!=)
                {
                    q[++t]=tmp;
                    vis[tmp]=;
                }
            }
        }
    }
}
int main()
{
    freopen("1.in","r",stdin);
    k=read();m=read();n=read();
    memset(b,,sizeof(b));
    for(int i=;i<=k;i++){int x;x=read();b[x]++;}
    for(int i=;i<=n;i++)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);
        add(y,x,z);
    }
    for(int i=;i<=m;i++)
    {
        int ans=;
        spfa(i);
        for(int j=;j<=m;j++)
        {
            if(b[j]!=)
                ans+=dis[j]*b[j];
        }
        minn=min(ans,minn);
    }
    printf("%d\n",minn);
    return ;
}

思路很清晰的打完了哈哈。

莫听穿林打叶声，何妨吟啸且徐行。