[CQOI2017]老C的方块 网络流

～～～题面～～～

题解：

做这题做了好久，，，换了4种建图QAQ

首先我们观察弃疗的形状，可以发现有一个特点，那就是都以一个固定不变的特殊边为中心的，如果我们将特殊边两边的方块分别称为s块和t块，

那么我们可以观察到，s块和t块永远是在中心位置，而其他两块则是紧邻s块和t块，一边一个。

所以我们要考虑将这个图像用一根线串起来，这样跑最小割才能割最小的边，

那么如何做到一条边割几个图形呢？

首先我们观察到一个非st方块本来就可以属于多个图形，因此也会有多条连边，因此我们只需要对每个方块拆点，限制其只能割一次就可以了。

一开始我选择的连图方式是：

以特殊边左边为s块，右边为t块，s连向s块，t块连向t（s块和t块名字来源），s块连向四周的非t块，t块四周的非s块连向它，s块四周的非t块连向t块四周的非s块。

但这样为什么这样不行呢？

我们可以观察到这样一种情况，

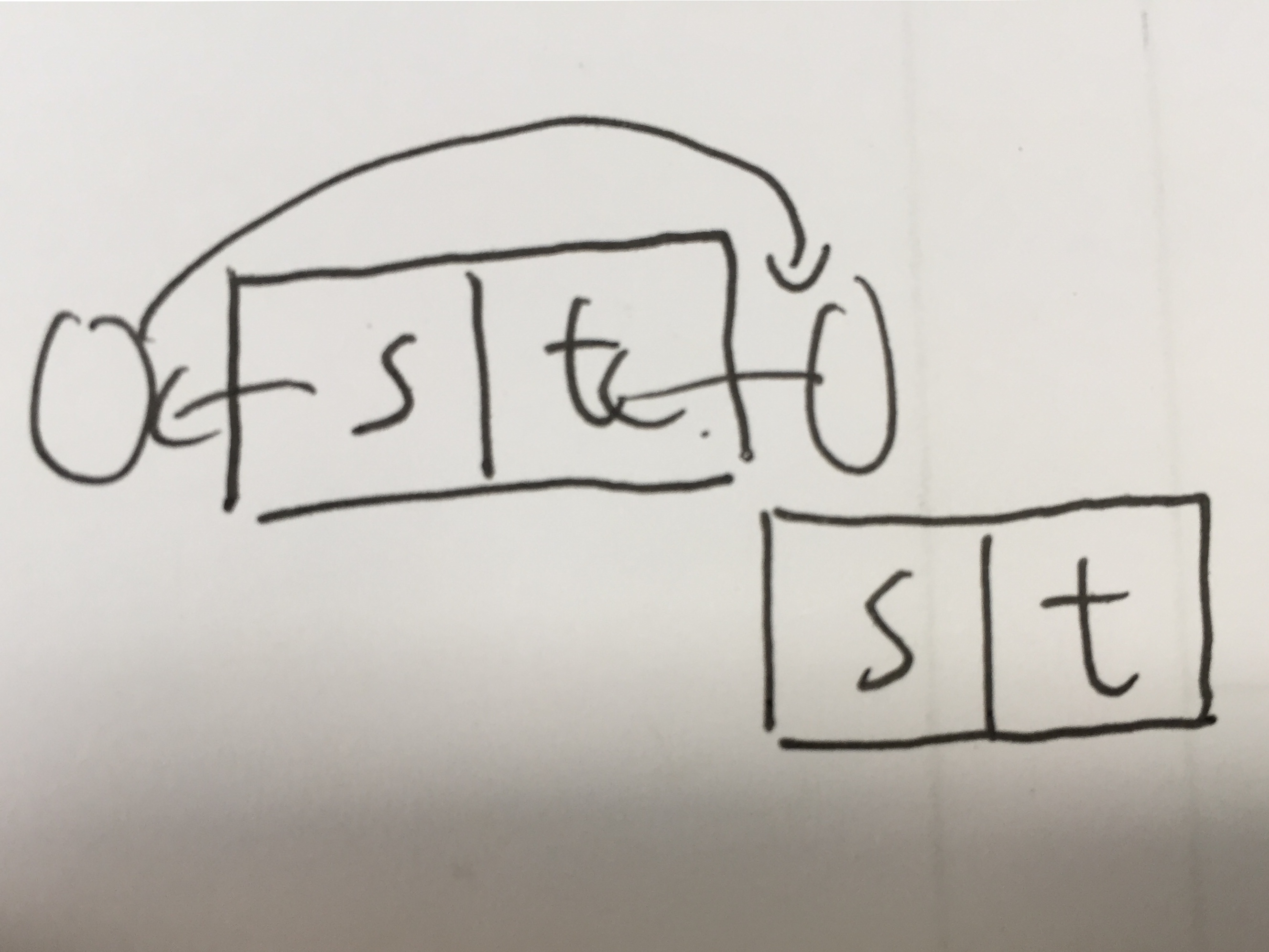
可以发现，右边的小圆圈同时处在s块和t块周围，那么由于扮演了两个角色，这就有可能导致右边的s块的流量流到左边的t块里，于是就出现了不合法情况。

…………

遂交换偶行的s块和t块。

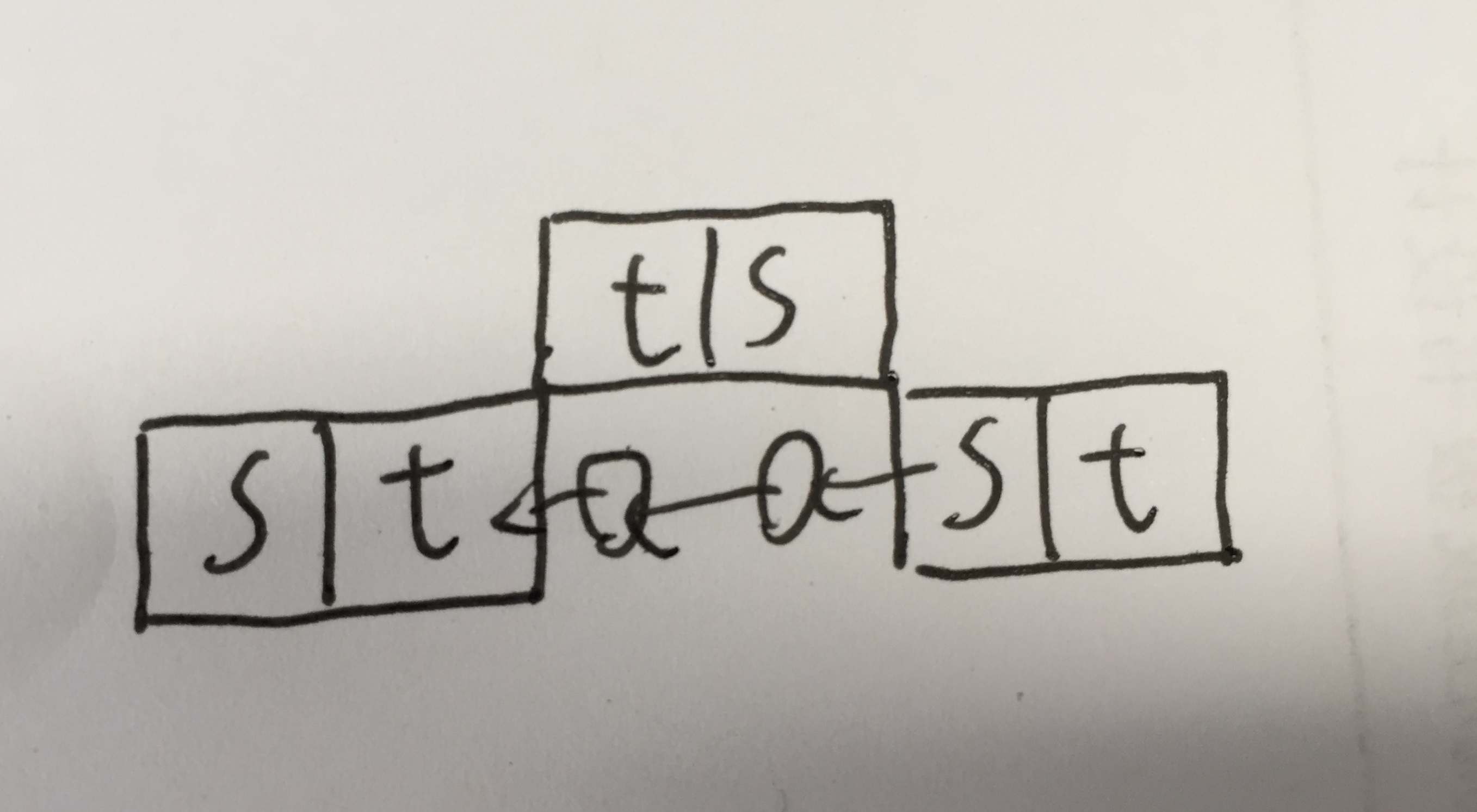
可以发现，右边的s块和左边的t块构成了一个不合法图形，那么这是为什么？

显然是上面反过来的t块和s块在勾桥搭线。。。。

那怎么办？

我们再观察一下图形。既然所有图形都是以s块和t块为中心，那么这两块显然是更加稳定的，因此我们不再用其他块作为中转块，而是采用以s块和t块为中转。

即：

s ---> s块周围的块 ----> s块 ---> t块 ---> t块周围的块

经验证，可以满足要求。

我是强行暴力人工分类讨论建图的。。。因此代码很长，建图就有60行。。。。

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define inf 2139062143
 #define getchar() *o++
 #define AC 200100
 #define ac 1700000

 char READ[], *o = READ;
 int n, x, ans, s, t, addflow, X, Y;
 int last[AC], good[AC], have[AC], c[AC], power[AC];
 int q[AC], head, tail;
 int date[ac], Next[ac], haveflow[ac], Head[AC], tot = ;

 struct point{
     int x, y;
 }p[AC];

 bool operator < (point a, point b)
 {
     if(a.x != b.x) return a.x < b.x;
     else return a.y < b.y;
 }

 map<point, int> m;

 inline int read()
 {
     int x=;char c=getchar();
     while(c > '' || c < '') c = getchar();
     while(c >= '' && c <= '') x=x*+c-'',c=getchar();
     return x;
 }

 inline void add(int f, int w, int S)
 {
     date[++tot] = w, Next[tot] = Head[f], haveflow[tot] = S, Head[f] = tot;
     date[++tot] = f, Next[tot] = Head[w],/* haveflow[tot] = 0,*/ Head[w] = tot;
 //    printf("%d ---> %d %d\n", f, w, S);
 }

 void pre()
 {
     X = read(), Y = read(), n = read();
     s = n *  + , t = s + ;
     for(R i=;i<=n;i++)
     {
         p[i].y = read(), p[i].x = read(), power[i] = read();//注意行列是反的！
         m[p[i]] = i;//编号
     }
 }

 void build()//暴力枚举加边
 {
     int x, y;
     for(R i=;i<=n;i++)//枚举方块，只连出边
     {
         add(i, n + i, power[i]);//拆点连边
         x = p[i].x, y = p[i].y;
         if(x % )//按奇偶行分类
         {
             if(y % )//按奇偶列分类（可能为s or t右）
             {//因为2 = 2 * 1, 6 = 2 * 3 .... 所以有余数就说明是s
                 if(((y + ) / ) % )//有余数所以是s
                 {//跟旁边的t连上
                     if(m[(point){x, y + }]) add(i + n, m[(point){x, y + }], inf);
                 }
                 else add(i + n, t, inf);//不然就要连向t了
             }
             else//不然就是s左的 or t
             {
                 if((y / ) % )
                 {
                     if(m[(point){x, y + }]) add(i + n, m[(point){x, y + }], inf);//如果有余数说明是t
                     if(m[(point){x + , y}]) add(i + n, m[(point){x + , y}], inf);
                     if(m[(point){x - , y}]) add(i + n, m[(point){x - , y}], inf);
                 }
                 else//不然属于s周围的
                 {
                     if(m[(point){x, y + }]) add(i + n, m[(point){x, y + }], inf);
                     if(m[(point){x + , y}]) add(i + n, m[(point){x + , y}], inf);
                     if(m[(point){x - , y}]) add(i + n, m[(point){x - , y}], inf);
                     add(s, i, inf);//注意s周围的要连s
                 }
             }
         }
         else //偶行
         {
             if(y % )//奇列，t or s右
             {
                 if(((y + ) / ) % )//如果有余数说明是s右
                 {
                     if(m[(point){x, y - }]) add(i + n, m[(point){x, y - }], inf);
                     if(m[(point){x + , y}]) add(i + n, m[(point){x + , y}], inf);
                     if(m[(point){x - , y}]) add(i + n, m[(point){x - , y}], inf);
                     add(s, i, inf);
                 }
                 else
                 {
                     if(m[(point){x, y - }]) add(i + n, m[(point){x, y - }], inf);//如果有余数说明是t
                     if(m[(point){x + , y}]) add(i + n, m[(point){x + , y}], inf);
                     if(m[(point){x - , y}]) add(i + n, m[(point){x - , y}], inf);
                 }
             }
             else//t左 or s
             {
                 if((y / ) % )    add(i + n, t, inf);//如果有余数的话，说明是t左
                 else//不然就是s
                     if(m[(point){x, y - }]) add(i + n, m[(point){x, y - }], inf);
             }//注意加了n才是出发点
         }
     }
 }

 void bfs()
 {
     int x, now;
     c[t] = , x = t, q[++tail] = t;
     while(head < tail)
     {
         x = q[++head];
         for(R i=Head[x]; i; i=Next[i])
         {
             now = date[i];
             if(haveflow[i^] && !c[now])
             {
                 ++have[c[now] = c[x] + ];
                 q[++tail] = now;
             }
         }
     }
     memcpy(good, Head, sizeof(Head));
 }

 inline void aru()
 {
     while(x != s)
     {
         haveflow[last[x]] -= addflow;
         haveflow[last[x] ^ ] += addflow;
         x = date[last[x] ^ ];
     }
     ans += addflow;
 }

 void isap()
 {
     int now; bool done;
     addflow = inf, x = s;
     while(c[s] != )
     {
         if(x == t) aru(), addflow = inf;
         done = false;
         for(R i =good[x]; i ;i =Next[i])
         {
             now = date[i];
             if(haveflow[i] && c[now] == c[x] -)
             {
                 addflow = min(addflow, haveflow[i]);
                 last[now] = i;
                 good[x] = i;
                 done = true;
                 x = now;
                 break;
             }
         }
         if(!done)
         {
             int go = ;
             for(R i=Head[x]; i ;i=Next[i])
             {
                 now = date[i];
                 if(haveflow[i] && c[now]) go = min(go, c[now]);
             }
             good[x] = Head[x];
             if(!(--have[c[x]])) break;
             ++have[c[x] = go + ];
             if(x != s) x = date[last[x] ^ ];
         }
     }
     printf("%d\n", ans);
 }

 int main()
 {
 //    freopen("in.in","r",stdin);
     fread(READ, , , stdin);
     pre();
     build();
     bfs();
     isap();
 //    fclose(stdin);
     return ;
 }