App Center编译React Native平台Android应用

做React Native一段时间后，对于React Native的发布有一些了解，原本的方法都是在本地直接生成APK文件的，具体可以参考《react native 生成APK》

因为需要将这个React Native的应用交给其他同事，但其他的同事暂时还未完全掌握到React Native，所以在发布这一块儿，需要使用一个工具帮助打包应用，在网上找了一些资料，目前做的比较好的就是微软公司的App Center

关于App Center（它是一个收费的云应用，在一定的限额内，应该还是免费的）：https://azure.microsoft.com/en-us/services/app-center/ 中文（https://azure.microsoft.com/zh-cn/services/app-center/）

本文章我只使用App Center的Build功能，只是将应用打包成APK即可，不会使用App Center的完整功能。

1.首先，在github创建一个空的项目ReactNativeAppForAppCenter，生成的地址就是，https://github.com/ChenWes/ReactNativeAppForAppCenter

2.另外，创建一个项目，使用命令创建一个React Native项目

react-native init ReactNativeAppForAppCenter --version 0.56.
cd ReactNativeAppForAppCenter

将项目放至github中

git init
git add .
git commit -m "project init"

git remote add origin https://github.com/ChenWes/ReactNativeAppForAppCenter
git push origin master #此处应该需要输入github的用户名及口令，验证成功后可以将代码同步至github上

3.最后，还需要生成一个keystore，关于如何生成keystore，可以参考react native官方文档：https://facebook.github.io/react-native/docs/signed-apk-android

---

再接下来配置App Center

登陆至App Center中，选择项目中，点击“Add new app”按钮，可以创建一个新的应用

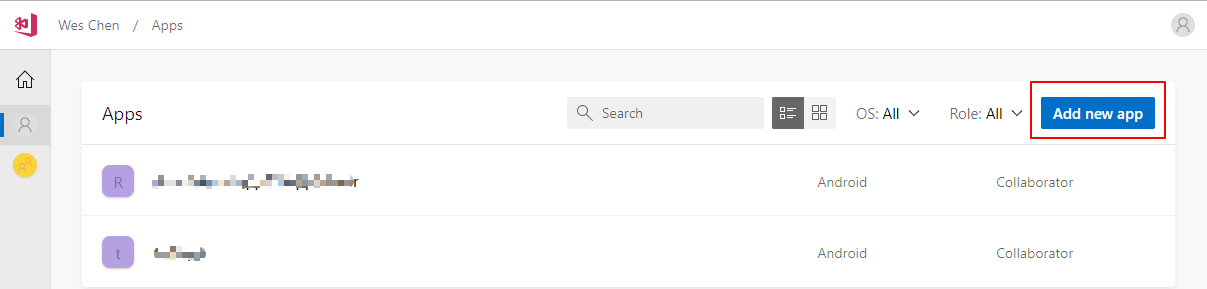
在弹出的“Add new app”窗口中选择“Android”系统和"React Native"平台，输入应用名称，点击"Add new app"按钮，即会创建一个新应用

点击应用左侧的Build选项，并选择github创建我们的代码仓库

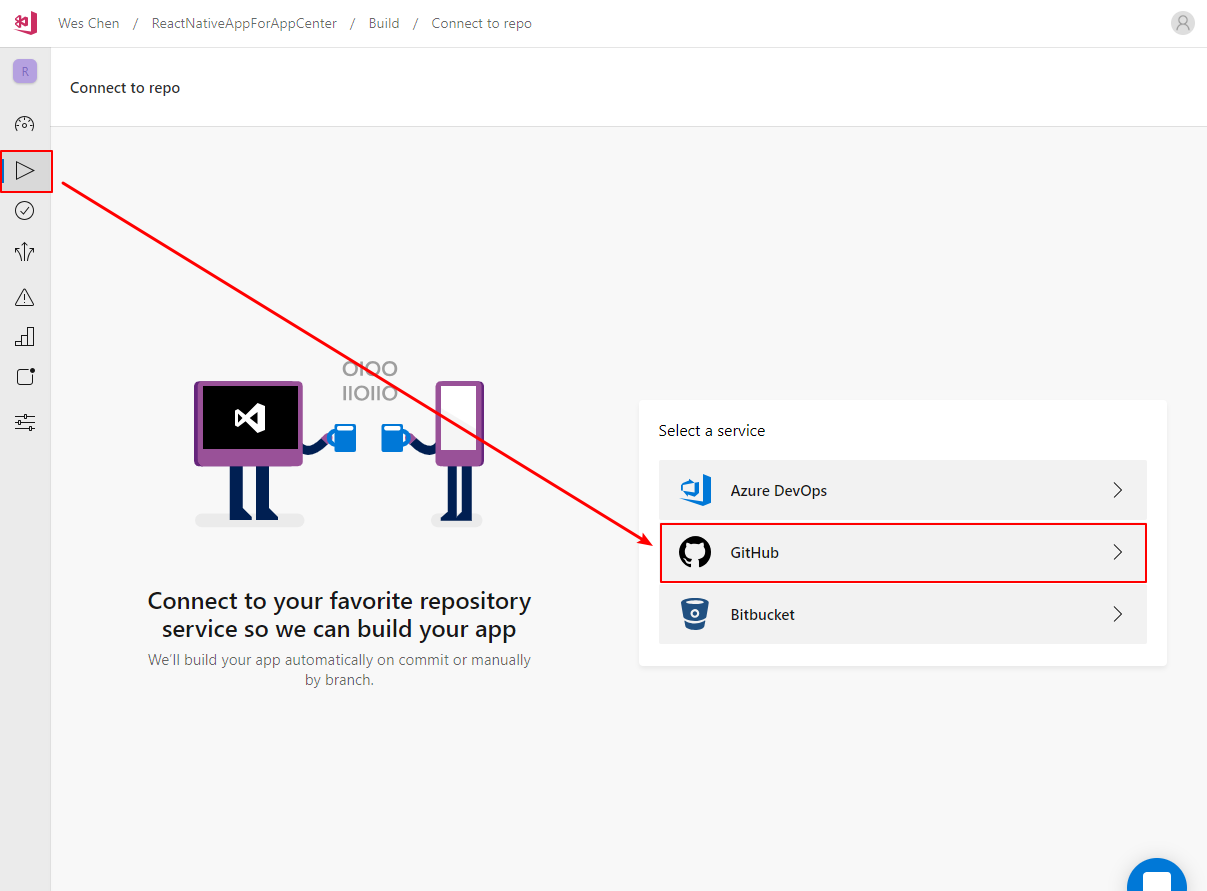
选择刚才的github仓库

关联了github代码仓库后的应用，当鼠标移动到其中一个branch上时，会显示一个齿轮的图标，点击后，可以能项目进行配置

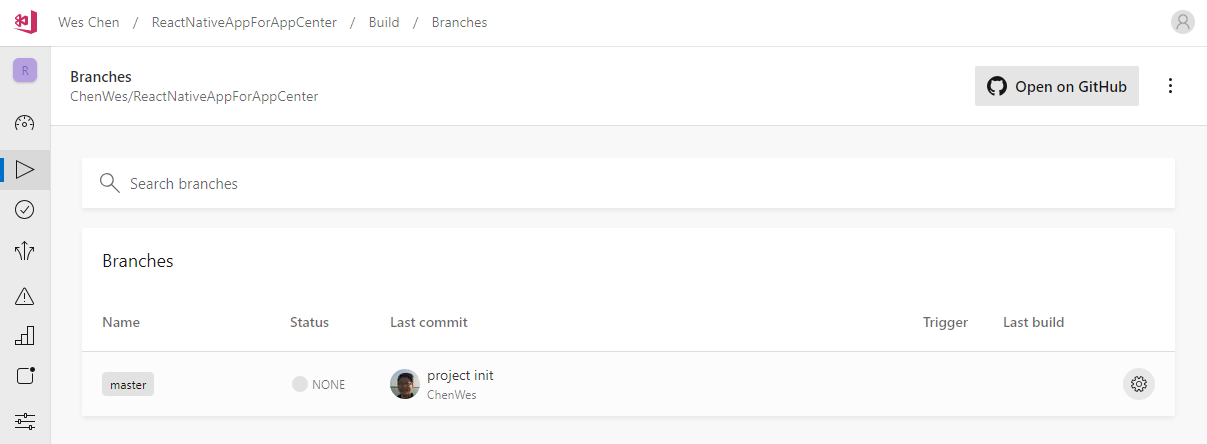
默认的设置如下，需要点击Sign builds，然后

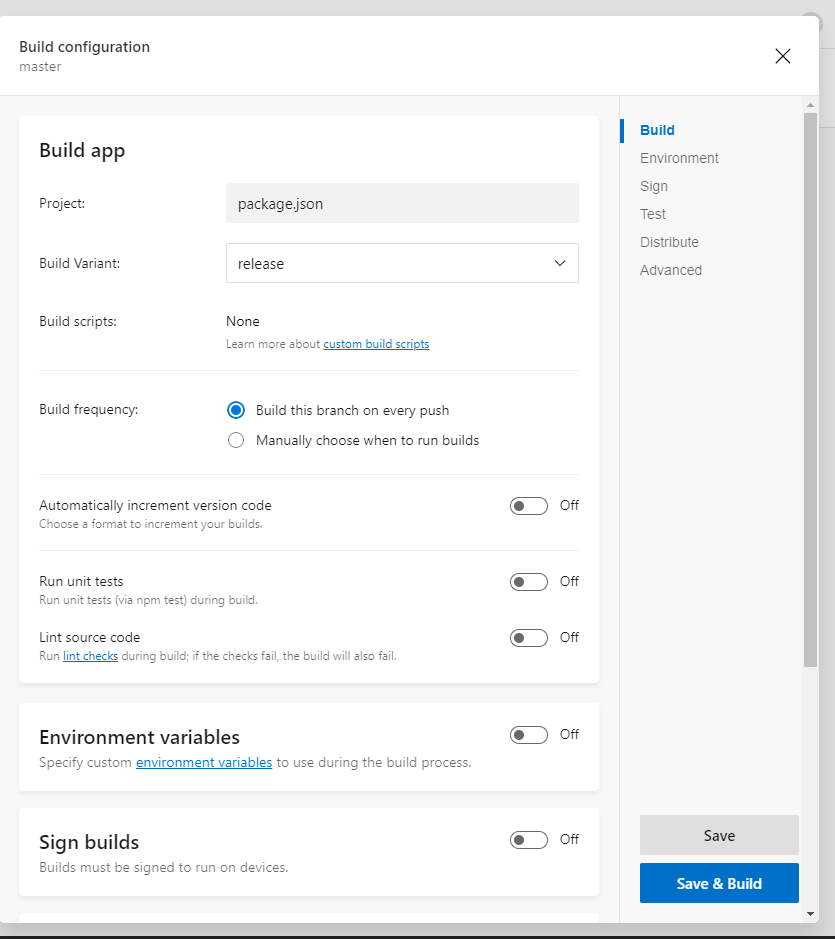
在这里，需要选择一个生成的keystore，输入对应的密码，点击右侧的"Save"按钮，配置就生效了，关于如何生成keystore，可以参考react native官方文档：https://facebook.github.io/react-native/docs/signed-apk-android

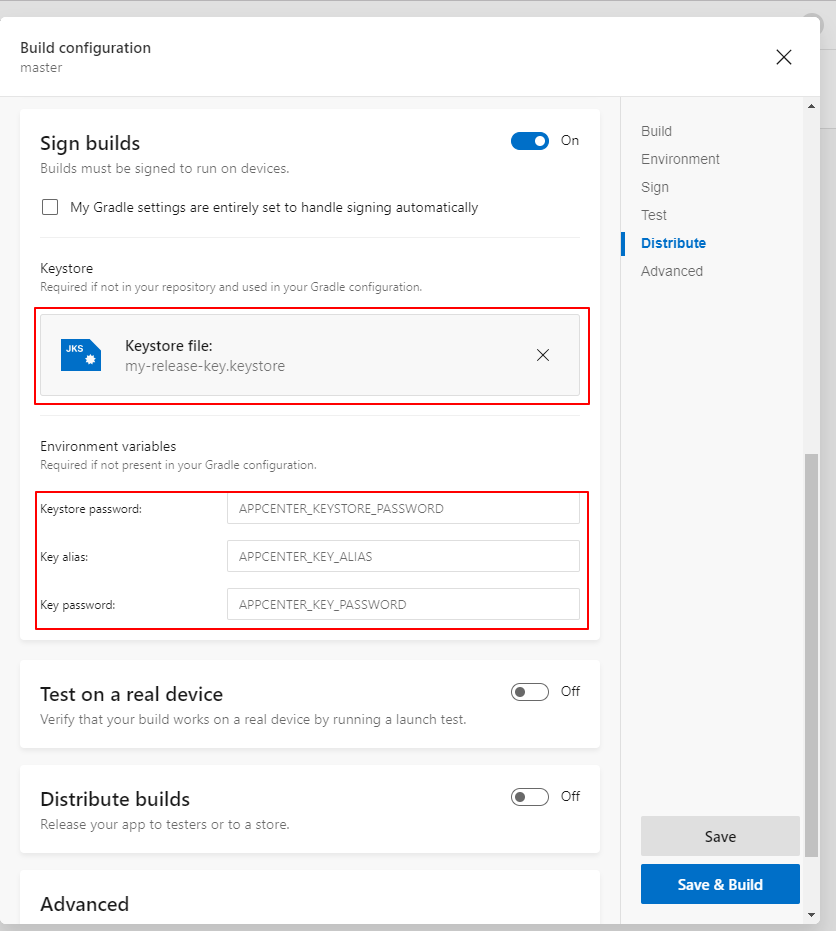
当保存了配置后，点击选择当前Branch名master，进入以下界面，点击"Build now"按钮即可，接下来需要等待服务器分配机器去build项目

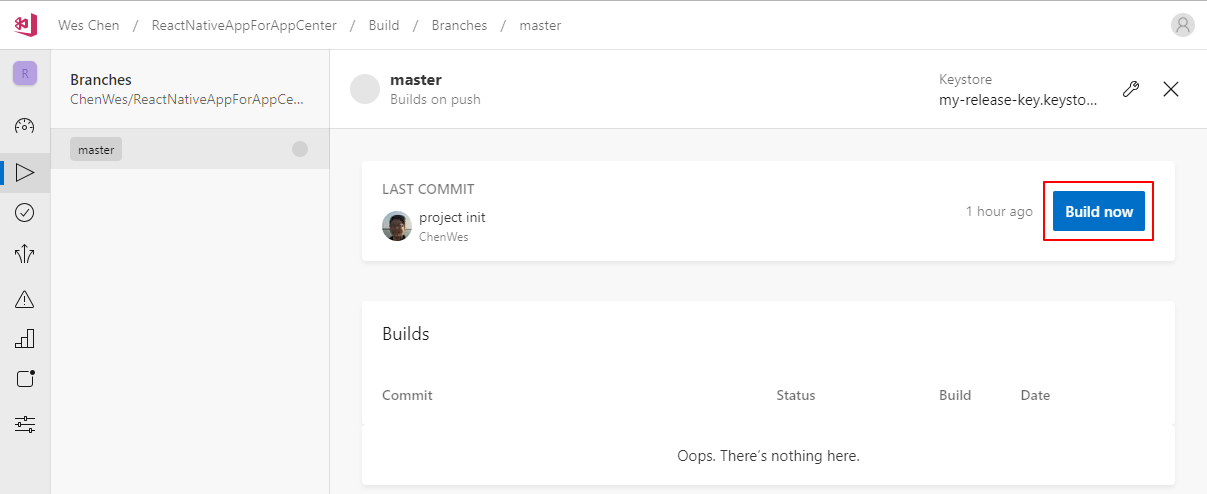
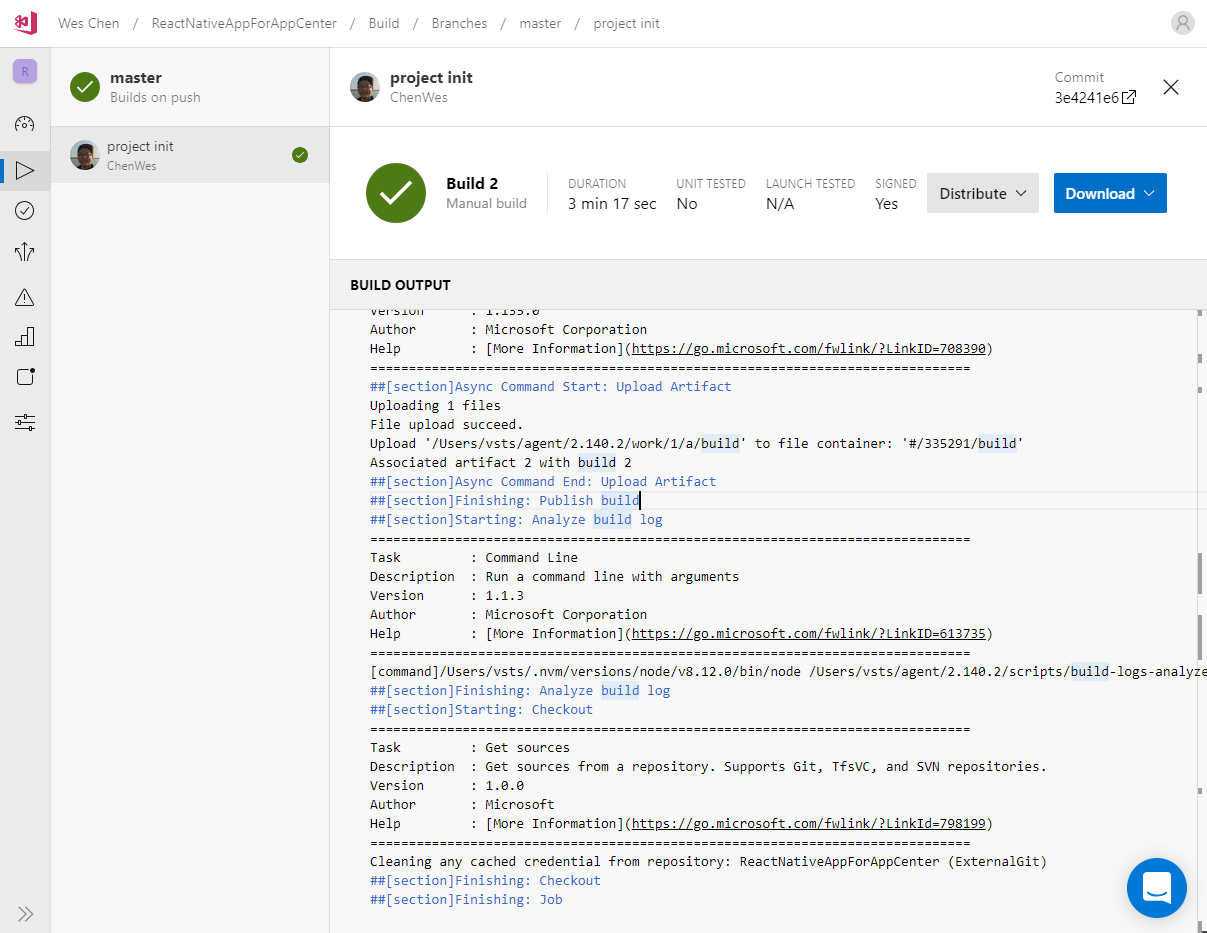
在build的同时也可以看到编译的日志信息，编译完成后，可以看到右上角有一个“Download"按钮，可以直接下载压缩文件，解压后，会得到一个app-release.apk文件