Educational Codeforces Round 41 (Rated for Div. 2) ABCDEF

最近打的比较少。。。就只有这么点题解了。

A. Tetris

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a following process.

There is a platform with n columns. 1 × 1 squares are appearing one after another in some columns on this platform. If there are no squares in the column, a square will occupy the bottom row. Otherwise a square will appear at the top of the highest square of this column.

When all of the n columns have at least one square in them, the bottom row is being removed. You will receive 1 point for this, and all the squares left will fall down one row.

You task is to calculate the amount of points you will receive.

Input

The first line of input contain 2 integer numbers n and m (1 ≤ n, m ≤ 1000) — the length of the platform and the number of the squares.

The next line contain m integer numbers c1, c2, ..., cm (1 ≤ ci ≤ n) — column in which i-th square will appear.

Output

Print one integer — the amount of points you will receive.

Example

input

Copy

3 9
1 1 2 2 2 3 1 2 3

output

2

---

题意：类似俄罗斯方块，不过每次只降下一个1*1的方块。给出列数，还有每次方块降下所在的列，求能消除几列。

题解：算每列方块数然后求最小值。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e3+;
 int a[N],n,m,d,minx;
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d",&d);
         a[d]++;
     }
     minx=INF;
     for(int i=;i<=n;i++)
         minx=min(minx,a[i]);
     printf("%d\n",minx);
     return ;
 }

B. Lecture Sleep

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Your friend Mishka and you attend a calculus lecture. Lecture lasts n minutes. Lecturer tells ai theorems during the i-th minute.

Mishka is really interested in calculus, though it is so hard to stay awake for all the time of lecture. You are given an array t of Mishka's behavior. If Mishka is asleep during the i-th minute of the lecture then ti will be equal to 0, otherwise it will be equal to 1. When Mishka is awake he writes down all the theorems he is being told — ai during the i-th minute. Otherwise he writes nothing.

You know some secret technique to keep Mishka awake for k minutes straight. However you can use it only once. You can start using it at the beginning of any minute between 1 and n - k + 1. If you use it on some minute i then Mishka will be awake during minutes j such that 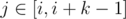 and will write down all the theorems lecturer tells.

You task is to calculate the maximum number of theorems Mishka will be able to write down if you use your technique only once to wake him up.

Input

The first line of the input contains two integer numbers n and k (1 ≤ k ≤ n ≤ 105) — the duration of the lecture in minutes and the number of minutes you can keep Mishka awake.

The second line of the input contains n integer numbers a1, a2, ... an (1 ≤ ai ≤ 104) — the number of theorems lecturer tells during the i-th minute.

The third line of the input contains n integer numbers t1, t2, ... tn (0 ≤ ti ≤ 1) — type of Mishka's behavior at the i-th minute of the lecture.

Output

Print only one integer — the maximum number of theorems Mishka will be able to write down if you use your technique only once to wake him up.

Example

input

Copy

6 3
1 3 5 2 5 4
1 1 0 1 0 0

output

16

Note

In the sample case the better way is to use the secret technique at the beginning of the third minute. Then the number of theorems Mishka will be able to write down will be equal to 16.

---

题意：第一行给出长度为n的价值序列，以及第二行可否获取的01序列，你可以最多把01序列里面连续k个置为1，问最多能获得多少价值。

题解:可获取的序列a[i]直接加入贡献，并置a[i]为0。然后求a[i]前缀和pre[i]，找一个最大的pre[i]-pre[i-k]加入贡献，这样的贡献即为答案。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 int a[N],t,n,m,d,maxn,k,ans,now;
 int main()
 {
     scanf("%d%d",&n,&k);
     for(int i=;i<=n;i++)
         scanf("%d",a+i);
     for(int i=;i<=n;i++)
     {
          scanf("%d",&t);
          if(t)
          {
              ans+=a[i];
              a[i]=;
          }
     }
     for(int i=;i<=k && i<=n;i++)
         now+=a[i];
     maxn=now;
     for(int i=k+;i<=n;i++)
     {
         now-=a[i-k];
         now+=a[i];
         maxn=max(maxn,now);
     }
     ans+=maxn;
     printf("%d\n",ans);
     return ;

 }

C. Chessboard

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Magnus decided to play a classic chess game. Though what he saw in his locker shocked him! His favourite chessboard got broken into 4pieces, each of size n by n, n is always odd. And what's even worse, some squares were of wrong color. j-th square of the i-th row of k-th piece of the board has color ak, i, j; 1 being black and 0 being white.

Now Magnus wants to change color of some squares in such a way that he recolors minimum number of squares and obtained pieces form a valid chessboard. Every square has its color different to each of the neightbouring by side squares in a valid board. Its size should be 2n by2n. You are allowed to move pieces but not allowed to rotate or flip them.

Input

The first line contains odd integer n (1 ≤ n ≤ 100) — the size of all pieces of the board.

Then 4 segments follow, each describes one piece of the board. Each consists of n lines of n characters; j-th one of i-th line is equal to 1 if the square is black initially and 0 otherwise. Segments are separated by an empty line.

Output

Print one number — minimum number of squares Magnus should recolor to be able to obtain a valid chessboard.

Examples

input

Copy

1
0

0

1

0

output

1

input

Copy

3
101
010
101

101
000
101

010
101
011

010
101
010

output

2

---

题意：有一个黑白相间的棋盘碎成4个n*n的块，而且其上的颜色沾污了，不一定是黑白相间的。现在让你把这4个块染色，给块中一格染色需要付出代价1。现在让你求使得这四块能拼成一个黑白相间的棋盘所需付出的最小代价。

题解：每个块染色后都有两种样式，分别对应左上角为黑或白。我们把每块变为这两种样式所需代价求出，然后枚举所有的4个块拼成棋盘的组合，找出最小的代价即为答案。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 int need[][],n,m,ans;
 char s[N];
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=;i++)
     {
         for(int j=;j<=n;j++)
         {
             scanf("%s",s);
             for(int k=;k<n;k++)
             {
                 m=s[k]-'';
                 need[i][(k&)^(j&)^m]++;
             }
         }
     }
     ans=INF;
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
             if(j!=i)
                 for(int k=;k<=;k++)
                     if(k!=j && k!=i)
                         for(int l=;l<=;l++)
                             if(l!=k && l!=j && l!=i)
                             {
                                 ans=min(ans,need[i][]+need[j][]+need[k][]+need[l][]);
                             }
     printf("%d\n",ans);
     return ;
 }

D. Pair Of Lines

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n points on Cartesian plane. Every point is a lattice point (i. e. both of its coordinates are integers), and all points are distinct.

You may draw two straight lines (not necessarily distinct). Is it possible to do this in such a way that every point lies on at least one of these lines?

Input

The first line contains one integer n (1 ≤ n ≤ 105) — the number of points you are given.

Then n lines follow, each line containing two integers xi and yi (|xi|, |yi| ≤ 109)— coordinates of i-th point. All n points are distinct.

Output

If it is possible to draw two straight lines in such a way that each of given points belongs to at least one of these lines, print YES. Otherwise, print NO.

Examples

input

Copy

5
0 0
0 1
1 1
1 -1
2 2

output

YES

input

Copy

5
0 0
1 0
2 1
1 1
2 3

output

NO

Note

In the first example it is possible to draw two lines, the one containing the points 1, 3 and 5, and another one containing two remaining points.

---

题意：给你一堆整数点，然后让你判断是否能最多只画两条直线，使得这两条直线经过所有点。

题解：先找到互不在同一直线上的三个点。然后枚举其中两个点连线，为其中一条直线。另外一个点找不在这条直线上的另一个点连线（用向量积），构成另外一条直线。然后检查所有点是不是在这两条线上，如果是的话就输出YES反之输出NO。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define ll long long
 using namespace std;
 const int maxn=1e5+;
 struct node{
     int x,y;
 }p[maxn];
 int res[];
 int n;
 void Read(){
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         scanf("%d%d",&p[i].x,&p[i].y);
     }
 }
 bool judge(int a,int b){
     int ans=;
     while(ans==a||ans==b) ans++;
     int y1=p[res[b]].y-p[res[a]].y;
     int x1=p[res[b]].x-p[res[a]].x;
     int x2,y2;
     bool flag=true;
     for(int i=;i<=n;i++){
         int y=p[i].y-p[res[a]].y;
         int x=p[i].x-p[res[a]].x;
         if(1LL*y1*x==1LL*x1*y)continue;
         y=p[i].y-p[res[ans]].y;
         x=p[i].x-p[res[ans]].x;
         if(flag&&i!=res[ans]){
             y2=y;x2=x;flag=false;
         }
         else{
             if(y2*x==x2*y)continue;
             return false;
         }
     }
     return true;
 }
 int main()
 {
     Read();
     if(n<=){
         printf("YES\n");
         return ;
     }
     int y1=p[].y-p[].y;
     int x1=p[].x-p[].x;
     int flag=;
     int i=;
     for(;i<=n;i++){
         int y=p[i].y-p[].y;
         int x=p[i].x-p[].x;
         if(1LL*y1*x==1LL*x1*y)
             continue;
         else{
             flag=;
             break;
         }
     }
     if(!flag){
         printf("YES\n");
         return ;
     }
     res[]=,res[]=,res[]=i;
     for(i=;i<;i++)
         for(int j=i+;j<;j++)
             if(judge(i,j)){
                 printf("YES\n");
                 return ;
             }
     printf("NO\n");
     return ;
 }

E. Tufurama

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

One day Polycarp decided to rewatch his absolute favourite episode of well-known TV series "Tufurama". He was pretty surprised when he got results only for season 7 episode 3 with his search query of "Watch Tufurama season 3 episode 7 online full hd free". This got Polycarp confused — what if he decides to rewatch the entire series someday and won't be able to find the right episodes to watch? Polycarp now wants to count the number of times he will be forced to search for an episode using some different method.

TV series have n seasons (numbered 1 through n), the i-th season has ai episodes (numbered 1 through ai). Polycarp thinks that if for some pair of integers x and y (x < y) exist both season x episode y and season y episode x then one of these search queries will include the wrong results. Help Polycarp to calculate the number of such pairs!

Input

The first line contains one integer n (1  ≤ n  ≤  2·105) — the number of seasons.

The second line contains n integers separated by space a1, a2, ..., an (1 ≤ ai ≤ 109) — number of episodes in each season.

Output

Print one integer — the number of pairs x and y (x < y) such that there exist both season x episode y and season y episode x.

Examples

input

Copy

5
1 2 3 4 5

output

0

input

Copy

3
8 12 7

output

3

input

Copy

3
3 2 1

output

2

Note

Possible pairs in the second example:

1. x = 1, y = 2 (season 1 episode 2  season 2 episode 1);
2. x = 2, y = 3 (season 2 episode 3  season 3 episode 2);
3. x = 1, y = 3 (season 1 episode 3  season 3 episode 1).

In the third example:

1. x = 1, y = 2 (season 1 episode 2  season 2 episode 1);
2. x = 1, y = 3 (season 1 episode 3  season 3 episode 1).

---

题意，给出一些季度和每季度的最高章节数，现在让你找存在总点对数。其中如若存在第x季度的第y章节及第y季度的第x章节(x<y)，那么（x,y）算作一对。

题解：写一个主席树，对于每个i，在a[i]（a[i]若>n,a[i]=n）处权值+1。然后对于每个i，查询其第i+1~a[i]棵树间[i,n]的权值总和，加入答案。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;
 const int N=2e5+;
 struct seg
 {
     int l,r;
     int sum;
     int lt,rt;
 }tree[N<<];
 int root[N],cnt,n,a[N];
 LL ans;
 void init(int &i,int l,int r)
 {
     tree[++cnt]=(seg){l,r};
     i=cnt;
     if(l==r)
         return ;
     int mid=(l+r)>>;
     init(tree[i].lt,l,mid);
     init(tree[i].rt,mid+,r);
     return ;
 }
 void update(int &i,int pos,int val)
 {
     tree[++cnt]=tree[i];
     i=cnt;
     tree[i].sum+=val;
     if(tree[i].l==tree[i].r)
         return ;
     int mid=(tree[i].l+tree[i].r)>>;
     if(pos<=mid)
         update(tree[i].lt,pos,val);
      else
         update(tree[i].rt,pos,val);
      return ;
 }
 int query(int &i,int &j,int l,int r)
 {
     if(tree[i].l>=l && tree[i].r<=r)
         return tree[j].sum-tree[i].sum;
     int mid=(tree[i].l+tree[i].r)>>;
     int ans=;
     if(l<=mid)
         ans+=query(tree[i].lt,tree[j].lt,l,r);
     if(r>mid)
         ans+=query(tree[i].rt,tree[j].rt,l,r);
     return ans;
 }
 int main()
 {
     scanf("%d",&n);
     init(root[],,n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",a+i);
         if(a[i]>n) a[i]=n;
         update(root[i]=root[i-],a[i],);
     }
     for(int i=;i<=n;i++)
     if(a[i]>i)
     {
         ans+=1LL*query(root[i],root[a[i]],i,n);
     }
     printf("%I64d\n",ans);
     return ;
 }

F. k-substrings

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a string s consisting of n lowercase Latin letters.

Let's denote k-substring of s as a string subsk = sksk + 1..sn + 1 - k. Obviously, subs1 = s, and there are exactly 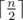 such substrings.

Let's call some string t an odd proper suprefix of a string T iff the following conditions are met:

• |T| > |t|;
• |t| is an odd number;
• t is simultaneously a prefix and a suffix of T.

For evey k-substring (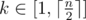) of s you have to calculate the maximum length of its odd proper suprefix.

Input

The first line contains one integer n (2 ≤ n ≤ 106) — the length s.

The second line contains the string s consisting of n lowercase Latin letters.

Output

Print 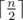 integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or  - 1, if there is no such string that is an odd proper suprefix of i-substring).

Examples

input

Copy

15
bcabcabcabcabca

output

Copy

9 7 5 3 1 -1 -1 -1

input

Copy

24
abaaabaaaabaaabaaaabaaab

output

Copy

15 13 11 9 7 5 3 1 1 -1 -1 1

input

Copy

19
cabcabbcabcabbcabca

output

Copy

5 3 1 -1 -1 1 1 -1 -1 -1

Note

The answer for first sample test is folowing:

• 1-substring: bcabcabcabcabca
• 2-substring: cabcabcabcabc
• 3-substring: abcabcabcab
• 4-substring: bcabcabca
• 5-substring: cabcabc
• 6-substring: abcab
• 7-substring: bca
• 8-substring: c

---

POI2012的一道原题Prefixuffix差不多，题解就不多说了，拿hash写写就能过了。

蟹蟹clairs的提点。顺便学了字符串hash。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 //usually mod num is 1004535809 99824435 1000000007
 #define pnum 233
 #define INF 0x3f3f3f3f
 #
 using namespace std;
 const int N=1e6+;
 int f[N],power[N][],hashx[N][],mod[]={,};
 inline int gethashx(int l,int r,int x)
 {
     return (hashx[r][x]-(LL)hashx[l-][x]*power[r-l+][x]%mod[x]+mod[x])%mod[x];
 }
 inline bool check(int x,int y,int len)
 {
     return gethashx(x,x+len-,)==gethashx(y,y+len-,) && gethashx(x,x+len-,)==gethashx(y,y+len-,);
 }
 int n,ans;
 char s[N];
 int main()
 {
     scanf("%d",&n);
     scanf("%s",s);
     power[][]=power[][]=;
     hashx[][]=hashx[][]=;
     for(int i=;i<=n;i++)
         for(int j=;j<;j++)
         {
             power[i][j]=(LL)power[i-][j]*pnum%mod[j];
             hashx[i][j]=((LL)hashx[i-][j]*pnum+(s[i-]-'a'))%mod[j];
         }
     for(int i=(n+)/;i>=;i--)
     {
         f[i]=min(f[i+]+,n-*i+);
         if(!(f[i]&))
             f[i]--;
         while(f[i]> && !check(i,n-i-f[i]+,f[i])) f[i]-=;
     }
     for(int i=;i<=(n+)/;i++)
         printf("%d ",f[i]);
     printf("\n");
     return ;
 }

另外一种方法就是求后缀数组+LCP+ST,这个麻烦点。两者区别就在于求子串相等部分的处理。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 #define mod 1000000007
 #define INF 0x3f3f3f3f
 #define F(x) ((x) / 3 + ((x) % 3 == 1 ? 0 : tb))
 #define G(x) ((x) < tb ? (x) * 3 + 1 : ((x) - tb) * 3 + 2)
 using namespace std;
 const int N=1e6+;
 int wa[N],wb[N],backet[N],order[N],sa[N*];
 int ranked[N],height[N],s[N*],n,f[N];
 char str[N];
 int c0(int *r,int a,int b)
 {
     return r[a]==r[b]&&r[a+]==r[b+]&&r[a+]==r[b+];
 }
 int c12(int k,int *r,int a,int b)
 {
     if(k==) return r[a]<r[b]||r[a]==r[b]&&c12(,r,a+,b+);
     else return r[a]<r[b]||r[a]==r[b]&&order[a+]<order[b+];
 }
 void sorted(int *r,int *a,int *b,int n,int m)
 {
     int i;
     for(i=;i<n;i++) order[i]=r[a[i]];
     for(i=;i<m;i++) backet[i]=;
     for(i=;i<n;i++) backet[order[i]]++;
     for(i=;i<m;i++) backet[i]+=backet[i-];
     for(i=n-;i>=;i--) b[--backet[order[i]]]=a[i];
     return;
 }
 void dc3(int *r,int *sa,int n,int m)
 {
     int i,j,*san=sa+n,ta=,tb=(n+)/,tbc=,p;
     int *rn=r+n;
     r[n]=r[n+]=;
     for(i=;i<n;i++) if(i%!=) wa[tbc++]=i;
     sorted(r+,wa,wb,tbc,m);
     sorted(r+,wb,wa,tbc,m);
     sorted(r,wa,wb,tbc,m);
     for(p=,rn[F(wb[])]=,i=;i<tbc;i++)
         rn[F(wb[i])]=c0(r,wb[i-],wb[i])?p-:p++;
     if(p<tbc) dc3(rn,san,tbc,p);
     else for(i=;i<tbc;i++) san[rn[i]]=i;
     for(i=;i<tbc;i++) if(san[i]<tb) wb[ta++]=san[i]*;
     if(n%==) wb[ta++]=n-;
     sorted(r,wb,wa,ta,m);
     for(i=;i<tbc;i++) order[wb[i]=G(san[i])]=i;
     for(i=,j=,p=;i<ta && j<tbc;p++)
         sa[p]=c12(wb[j]%,r,wa[i],wb[j])?wa[i++]:wb[j++];
     for(;i<ta;p++) sa[p]=wa[i++];
     for(;j<tbc;p++) sa[p]=wb[j++];
     return;
 }
 void calheight(int *r, int *sa, int n) {
     int i, j, k = ;
     for (i = ; i <= n; i++) ranked[sa[i]] = i;
     for (i = ; i < n; height[ranked[i++]] = k)
         for (k ? k-- : , j = sa[ranked[i] - ]; r[i + k] == r[j + k]; k++);
     return ;
 }
 int st[N][];
 void calmin(int n)
 {
     int t=,k,divk;
     for(int i=;i<n;i++)
         st[i][]=height[i+];
     for(k=,t=,divk=;k<=n;k<<=,divk<<=,t++)
         for(int i=;i<=n-k+;i++)
             st[i][t]=min(min(st[i][t-],st[i+divk][t-]),height[i+divk]);
     return ;
 }
 int getmin(int u,int v)
 {
     u=ranked[u];
     v=ranked[v];
     if(u>v) swap(u,v);
     int p=v-u+,k=;
     while(p)
     {
         p>>=;
         k++;
     }
     return min(st[u][k-],st[v-(<<k-)+][k-]);
 }
 int main()
 {
     scanf("%d",&n);
     scanf("%s",str);
     for(int i=;i<n;i++)
     {
         s[i]=str[i]-'a'+;
     }
     s[n]=;
     dc3(s,sa,n+,);
     calheight(s,sa,n);
     calmin(n);
     int t;
     for(int i=(n-)/;i>=;i--)
     {
         f[i]=min(f[i+]+,n-*i-);
         if(!(f[i]&))
             f[i]--;
         while(f[i]> && getmin(i,n-i-f[i])<f[i])
                 f[i]-=;
     }
     for(int i=;i<=(n-)/;i++)
         printf("%d ",f[i]);
     return ;
 }