【BZOJ 1478】 1478: Sgu282 Isomorphism （置换、burnside引理）

1478: Sgu282 Isomorphism

Description

给 定一个N 个结点的无向完全图（ 任意两个结点之间有一条边）， 现在你可以用 M 种颜色对这个图的每条边进行染色，每条边必须染一种颜色。 若两个已染色的图，其中一个图可以通过结点重新编号而与另一个图完全相同， 就称这两个染色方案相同。 现在问你有多少种本质不同的染色方法，输出结果 mod P。P 是一个大于N 的质数。

Input

仅一行包含三个数，N、M、P。

Output

仅一行，为染色方法数 mod P 的结果。

Sample Input

3 4 97

Sample Output

20

HINT

数据范围：1≤N≤53，1≤M≤1000，N

【分析】

　　关于这题，这文档讲得很清楚：http://wenku.baidu.com/view/fee9e9b9bceb19e8b8f6ba7a.html?from=search###

　　这题想起来挺难的。

　　首先它是对点的置换，但是是边染上了颜色，就是说实际上是边的置换。所以我们要看一下点置换和边置换之间的关系。

　　假定一个点置换，把它表示为循环，比如是(a1,a2,....)(b1,b2...)(c1,c2...)...

　　1、对于不在一个循环里面的点：

　　比如a1,b1, 那么会有边循环((a1,b1),(a2,b2)...) 设a循环的循环节是l1,b循环的循环节是l2,那么形成的边循环的循环节显然是LCM(l1,l2)。

　　一共有l1*l2个点对，每个点对都在一个循环节为LCM(l1,l2)的循环上，所以一共有l1*l2/LCM(l1,l2)=GCD(l1,l2)个循环节，所以C(f)=m^GCD(l1,l2)。（回到burnside引理，C为置换之后仍为本身的数目，就是说要循环节里的每条边都一样的颜色）

　　2、对于在一个循环里面的点：

　　比如a1、a2。设这个a循环的循环节为l1。

　　如果l1是奇数，那么循环长度为l1，一共有C(l1,2)个点对，所以是(l1-1)/2个循环节，所以C(f)=m^((l1-1)/2)。

　　如果l1是偶数，除了上面这种情况之外，还有一种的循环节是l1/2（就是两个点刚好相隔半个周期，而边是双向的），所以一共有(C(l1,2)-l1/2)/l1+1=l1/2个点对。

　　整理一下：

　　

　　

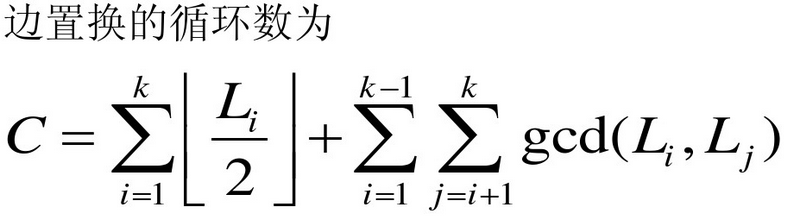
　　所以代码很简单，只要枚举n的拆分，然后计算不动点就好了。这里有用到逆元，p是质数可以用费马小定理。

　　分母上面先乘完再求逆元，我就是一边乘一边逆元就超时了。。。ORZ。。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 60
 #define LL long long

 int n,m;
 LL pw[Maxn],N,p,ans;

 LL qpow(LL a,LL b)
 {
     LL ans=;
     while(b)
     {
         if(b&) ans=(ans*a)%p;
         a=(a*a)%p;
         b>>=;
     }
     return ans;
 }

 LL l[Maxn];

 int gcd(int a,int b)
 {
     if(b==) return a;
     return gcd(b,a%b);
 }

 void get_ans(int x)
 {
     int c=;
     for(int i=;i<=x;i++) c+=l[i]/;
     for(int i=;i<=x;i++)
      for(int j=i+;j<=x;j++) c+=gcd(l[i],l[j]);
     LL now=;
     for(int i=;i<=x;i++) now=(now*l[i])%p;
     int cnt=;
     for(int i=;i<=x;i++)
     {
         if(l[i]!=l[i-])
         {
             now=(now*pw[cnt])%p;
             cnt=;
         }
         cnt++;
     }
     now=(now*pw[cnt])%p;
     now=(N*qpow(now,p-))%p;
     ans=(ans+now*qpow(m,c))%p;
     // printf("%d\n",ans);
 }

 void ffind(int x,int st,int h)
 {
     if(h==)
     {
         get_ans(x-);
     }
     if(h<st) return;
     for(int i=st;i<=h;i++)
     {
         l[x]=i;
         ffind(x+,i,h-i);
     }
 }

 int main()
 {
     scanf("%d%d%lld",&n,&m,&p);
     N=;
     for(int i=;i<=n;i++) N=(N*i)%p;
     pw[]=;
     for(int i=;i<=n;i++) pw[i]=(pw[i-]*i)%p;
     ans=;
     ffind(,,n);
     printf("%lld\n",(ans*qpow(N,p-))%p);
     return ;
 }

2017-01-12 11:34:31