CodeForces 450B

B. Jzzhu and Sequences

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Jzzhu has invented a kind of sequences, they meet the following property:

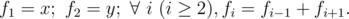
You are given x and y, please calculate f_n modulo 1000000007 (10⁹ + 7).

Input

The first line contains two integers x and y (|x|, |y| ≤ 10⁹). The second line contains a single integer n (1 ≤ n ≤ 2·10⁹).

Output

Output a single integer representing f_n modulo 1000000007 (10⁹ + 7).

Sample test(s)

Input

2 3
3

Output

1

Input

0 -1
2

Output

1000000006

Note

In the first sample, f₂ = f₁ + f₃, 3 = 2 + f₃, f₃ = 1.

In the second sample, f₂ =  - 1;  - 1 modulo (10⁹ + 7) equals (10⁹ + 6).

/**
          题意：f[i] = f[i-1] + f[i+1]
          做法：矩阵  如题要求建一个二维矩阵，
                    0   1
                   -1   0
                   然后求解
**/
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define SIZE 2
#define MOD 1000000007
#define clr( a, b ) memset( a, b, sizeof(a) )
typedef long long LL;

struct Mat
{
    LL mat[ SIZE ][ SIZE ];
    int n;
    Mat( int _n )
    {
        n = _n;
        clr( mat,  );
    }
    void init()
    {
        for( int i = ; i < n; ++i )
            for( int j = ; j < n; ++j )
                mat[i][j] = ( i == j );
    }
    Mat operator * ( const Mat &b ) const
    {
        Mat c( b.n );
        for( int k = ; k < n; ++k )
            for( int i = ; i < n; ++i )    if( mat[i][k] )
                    for( int j = ; j < n; ++j )
                        c.mat[i][j] = ( c.mat[i][j] + mat[i][k] * b.mat[k][j] ) % MOD;
        return c;
    }
};

Mat fast_mod( Mat a, int b )
{
    Mat res( a.n );
    res.init();
    while( b )
    {
        if( b &  ) res = res * a;
        a = a * a;
        b >>= ;
    }
    return res;
}

int main()
{
    LL x, y, n, res;
    scanf( "%lld %lld %lld", &x, &y, &n );
    if( n ==  )
    {
        printf( "%lld\n", ( x % MOD + MOD ) % MOD );
    }
    else if( n ==  )
    {
        printf( "%lld\n", ( y % MOD + MOD ) % MOD );
    }
    else
    {
        n -= ;
        Mat C(  );
        C.mat[][] = ;
        C.mat[][] = ;
        C.mat[][] = -;
        C.mat[][] = ;
        C = fast_mod( C, n );
        res = ( ( x * C.mat[][] + y * C.mat[][] )% MOD + MOD ) % MOD;
        printf( "%lld\n", res );
    }
    return ;
}