题解：2018级算法第五次上机 C5-图2

题目描述：

样例：

实现解释：

所有结点对最短路径的板子题

知识点：

寻找所有结点对最短路径，动态规划

坑点：

无坑，注意建边即可

使用的算法为floyd算法

按照程序顺序解释如下：

首先建图，以邻接矩阵形式，初始化矩阵内容：对i==j的设为权值0，其他的设为INF（正无穷的大小取决于题目），以便后续计算时能区分自身和不可达结点。然后依据输入按照edge[u][v] = w的形式连点即可。

运行floyd算法

动态规划思想展现：最优子结构，状态转移方程

以下图为例：（来源网络）

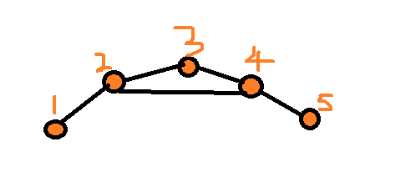
上图中1号到5号的最短路径序列<1,2,4,5>，其子序列<1,2,4>也是最短路径。以dp[k][i][j]表示以点1到k之间的点为媒介时，从i到j的最短路径。那么为了进行状态转移，需要和之前的dp建立关系，则对dp[k-1][i][j]可有以下的两种情况：

　　1.dp[k][i][j]的最短路不经过k

　　dp[k][i][j]=dp[k-1][i][j]

　　2.dp[k][i][j]的最短路经过k

　　dp[k][i][j]=dp[k-1][i][k]+dp[k-1][k][j]

则有状态转移方程

dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j])（k,i,j∈[1,n]）

边界条件即dp[0][i][j] = edge[i][j]

又从状态转移方程可看出，k只和k-1有关，因此可进行维度优化：

　　dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j])（k,i,j∈[1,n]）每次只需自身和另一种情况对比便可达到同样的效果。

　　则从分析可知，程序内容其实和矩阵链乘十分类似，初始化dp数组（dp[i][j]=edge[i][j]，边界条件）后，三层循环便可得到结果。

　　具体可见代码。

完整代码：

#include <iostream>
#include <string>
#include <stdio.h>
using namespace std;
#define MAX 210
#define INF 99999
int n,e;
int edges[MAX][MAX];
long long dp[MAX][MAX];
int path[MAX][MAX];
void createGraph()
{
    int u,v,w;
    cin >> n >> e;
    for(int i = ; i<n; i++)
    {
        for(int j = ; j<n; j++)
        {
            if(i == j) edges[i][j] = ;
            else edges[i][j] = INF;
        }
    }
    for(int i = ; i<e; i++)
    {
        cin >> u >> v >> w;
        edges[u-][v-] = w;
    }
}
void getPath()
{
    int from,to,length = -;
    for(int i = ;i<n;i++)
    {
        for(int j = ;j<n;j++)
        {
            if(dp[i][j] != INF)
            {
                if(dp[i][j]>length)
                {
                    from = i+;
                    to = j+;
                    length = dp[i][j];
                }
            }
        }
    }
    cout << from << ' ' << to << '\n';
}

void floyd()
{
    for(int i = ;i<n;i++)
    {
        for(int j = ;j<n;j++)
        {
            dp[i][j] = edges[i][j];
        }
    }
    for(int k = ;k<n;k++)
    {
        for(int i = ;i<n;i++)
        {
            for(int j = ;j<n;j++)
            {
                //抛去维度，直接计算
                if(dp[i][j] > dp[i][k]+dp[k][j])
                {
                    dp[i][j] = dp[i][k]+dp[k][j];
                    path[i][j] = k;
                }
            }
        }
    }
    getPath();
}
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        createGraph();
        floyd();
    }
    return ;
}