JPEG解码——(5)反量化和逆ZigZag变换

　　本篇是该系列的第五篇，承接上篇huffman解码，介绍接下来的两个步骤——反量化和逆zigzag变换，即IDCT前的两个步骤。

　　需要说明的是，这两个步骤可以颠倒，本人的实现是，先反量化，再逆ZigZag变换。

　　其实，这两步不需要太多说明，无非是查表对数据进行scale和数据重排，为了完整性，还是介绍一下吧。

1. 反量化

　　先拿到两个表，一个是解析文件头得到的量化表，另外一个是huffman解码得到的重建的8x8的block表。如下：

     

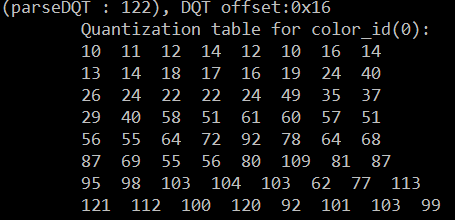
　　如何操作？对应位置相乘，即得到的反量化表：

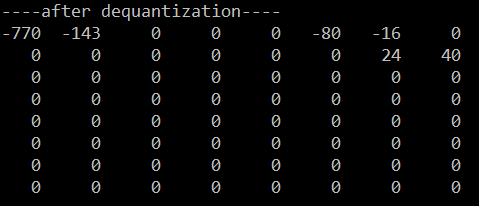
 2. 逆ZigZag变换

　　反量化表dequantization table是由如下ZigZag方式扫描得到的（忽略数字，关注箭头扫描方向）：

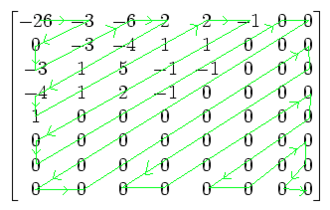
　　因此，需要对该表进行恢复，得到：

　　如何操作？无非是查表，可以参考下面的代码实现：

 1 static const uint8_t zigzag[64] =
 2 {
 3    0,  1,  5,  6, 14, 15, 27, 28,
 4    2,  4,  7, 13, 16, 26, 29, 42,
 5    3,  8, 12, 17, 25, 30, 41, 43,
 6    9, 11, 18, 24, 31, 40, 44, 53,
 7   10, 19, 23, 32, 39, 45, 52, 54,
 8   20, 22, 33, 38, 46, 51, 55, 60,
 9   21, 34, 37, 47, 50, 56, 59, 61,
10   35, 36, 48, 49, 57, 58, 62, 63
11 };
12
13 // IZigZag
14 int JpegReZigZag(struct ABitReader *abr, struct jpegParam *param, int *dst_block, const int *src_block, bool dump)
15 {
16     for (int i=0; i<64; i++) {
17         dst_block[i] = src_block[zigzag[i]];
18     }
19
20     if (dump) {
21         puts("----after rezigzag----");
22         for (int i=0; i<64; i++) {
23             printf("%4d  ", dst_block[i]);
24             if (i % 8 == 7)
25                 puts("");
26         }
27         puts("");
28     }
29
30     return 0;
31 }