C# 应用 - 多线程 1) 多线程的知识图谱
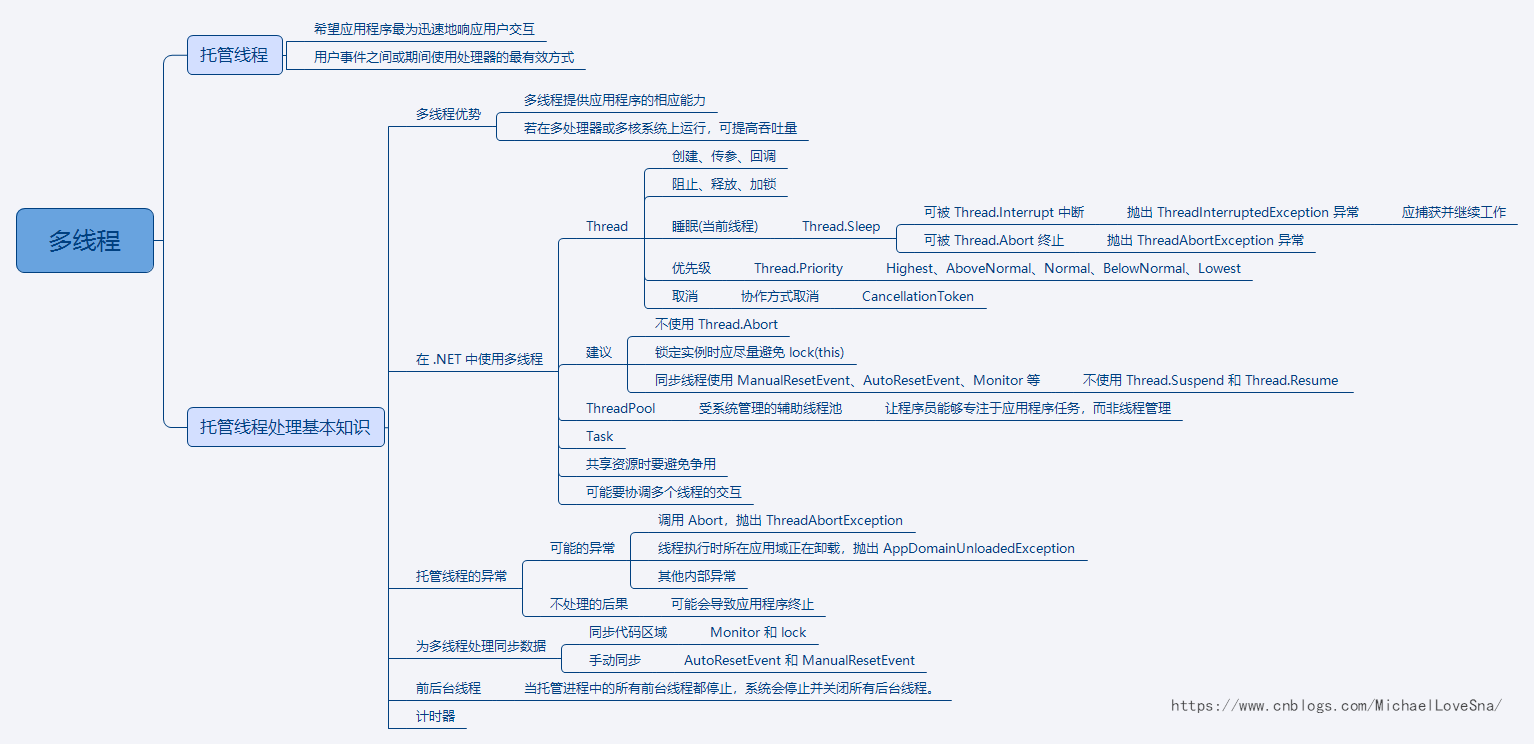
C# 应用 - 多线程 1) 多线程的知识图谱的更多相关文章
- Redis闲谈(1):构建知识图谱
场景:Redis面试 (图片来源于网络) 面试官: 我看到你的简历上说你熟练使用Redis,那么你讲一下Redis是干嘛用的? 小明: (心中窃喜,Redis不就是缓存吗?)Redis主要用作缓存,通 ...
- 知识图谱+Recorder︱中文知识图谱API与工具、科研机构与算法框架
目录 分为两个部分,笔者看到的知识图谱在商业领域的应用,外加看到的一些算法框架与研究机构. 文章目录 @ 一.知识图谱商业应用 01 唯品金融大数据 02 PlantData知识图谱数据智能平台 03 ...
- 不藏了,摊牌了,一张知识图谱整理完整Java并发体系,就问全不全
推荐阅读: 2020年马士兵Java多线程高并发讲解——百万年薪架构师告诉你Java多线程与高并发 目录 这是我关于整个Java并发体系的整理,结合的主要是现在市面上对于Java并发在面试的过程中经常 ...
- JavaSE 知识图谱
JAVA基础语法 DOS命令 JAVA介绍 JDK安装 JAVA环境的搭建 关键字 注释 标识符命名规则(编码规范) 字面值常量 进制转换 基本类型 变量(局部变量.静态变量) 运算符 表达式 控制语 ...
- Java多线程(一) 多线程的基本使用
在总结JDBC数据库连接池的时候,发现Java多线程这块掌握得不是很好,因此回头看了下多线程的内容.做一下多线程模块的学习和总结,稳固一下多线程这块的基础.关于多线程的一些理论知识,这里不想啰嗦太多, ...
- {python--GIL锁}一 介绍 二 GIL介绍 三 GIL与Lock 四 GIL与多线程 五 多线程性能测试
python--GIL锁 GIL锁 本节目录 一 介绍 二 GIL介绍 三 GIL与Lock 四 GIL与多线程 五 多线程性能测试 一 背景知识 ''' 定义: In CPython, the gl ...
- Atitit learn by need 需要的时候学与预先学习知识图谱路线图
Atitit learn by need 需要的时候学与预先学习知识图谱路线图 1. 体系化是什么 架构 知识图谱路线图思维导图的重要性11.1. 体系就是架构21.2. 只见树木不见森林21.3. ...
- Atitit 图像处理知识点体系知识图谱 路线图attilax总结 v4 qcb.xlsx
Atitit 图像处理知识点体系知识图谱 路线图attilax总结 v4 qcb.xlsx 分类 图像处理知识点体系 v2 qb24.xlsx 分类 分类 理论知识 图像金字塔 常用底层操作 卷积扫描 ...
- Atitit 补充说明 sql知识图谱与线路图attilax总结补充说明
Atitit 补充说明 sql知识图谱与线路图attilax总结补充说明 1. 常见编程语言的分类 :命令式语言.函数式语言.逻辑语言1 1.1. 按照编程语言的代际划分,又2gl,3gl,4gl ...
- iOS开发多线程篇—多线程简单介绍
iOS开发多线程篇—多线程简单介绍 一.进程和线程 1.什么是进程 进程是指在系统中正在运行的一个应用程序 每个进程之间是独立的,每个进程均运行在其专用且受保护的内存空间内 比如同时打开QQ.Xcod ...
随机推荐
- Redis性能指标监控
监控指标 •性能指标:Performance•内存指标: Memory•基本活动指标:Basic activity•持久性指标: Persistence•错误指标:Error 性能指标:Perform ...
- Redis 的缓存淘汰机制(Eviction)
本文从源码层面分析了 redis 的缓存淘汰机制,并在文章末尾描述使用 Java 实现的思路,以供参考. 相关配置 为了适配用作缓存的场景,redis 支持缓存淘汰(eviction)并提供相应的了配 ...
- 抓包 127.0.0.1 (loopback) 使用 tcpdump+wireshark
直接使用 wireshark无法抓取 127.0.0.1环回的数据包,一种解决方法是先传到路由器再返回,但这样可能造成拥塞. Linux 先使用tcpdump抓包并输出为二进制文件,然后wiresha ...
- 牛客网多校第4场 J Hash Function 【思维+并查集建边】
题目链接:戳这里 学习博客:戳这里 题意: 有n个空位,给一个数x,如果x%n位数空的,就把x放上去,如果不是空的,就看(x+1)%n是不是空的. 现在给一个已经放过数的状态,求放数字的顺序.(要求字 ...
- spring-cloud-netflix-eureka-server
一.构建springcloud父pom工程,管理版本 pom.xml <?xml version="1.0" encoding="UTF-8"?> ...
- postion:fixed和margin:0 auto的使用
很多同学将顶部菜单固定,使用postion:fixed,然后使用margin:0 auto进行居中,发现margin:0 auto并不起作用. 通常,我们要让某元素居中,会这样做: #element{ ...
- 使用 js 实现一个简易版的 drag & drop 库
使用 js 实现一个简易版的 drag & drop 库 具有挑战性的前端面试题 H5 DnD js refs https://www.infoq.cn/article/0NUjpxGrqRX ...
- 一个模块如何同时支持 ESM 和 CJS
一个模块如何同时支持 ESM 和 CJS 模块转化 webpack + babel refs xgqfrms 2012-2020 www.cnblogs.com 发布文章使用:只允许注册用户才可以访问 ...
- how to design a search component in react
how to design a search component in react react 如何使用 React 设计并实现一个搜索组件 实时刷新 节流防抖 扩展性,封装,高内聚,低耦合 响应式 ...
- css & box-shadow & outline
css & box-shadow & outline CSS3 box-shadow : 4 sides symmetry https://learning.xgqfrms.xyz/C ...
