【UV统计】海量数据统计的前世今生

转载请注明出处

背景

在互联网公司中，每个项目都需要数据统计、分析，便于项目组利用详细数据研究项目的整体情况，进行下一步的调整。在数据统计中，UV统计是最常见的，也是最普遍的。有的场景要求实时性很高，有点场景要求准确性很高，有的场景比较在意计算过程中的内存。不同的场景使用不同的算法，下面我们从0到1简单介绍下UV统计领域。

什么是UV统计

假设我们的场景是商家这边上架一系列水果，然后需要统计出一共上架几种水果。具体如下所示：

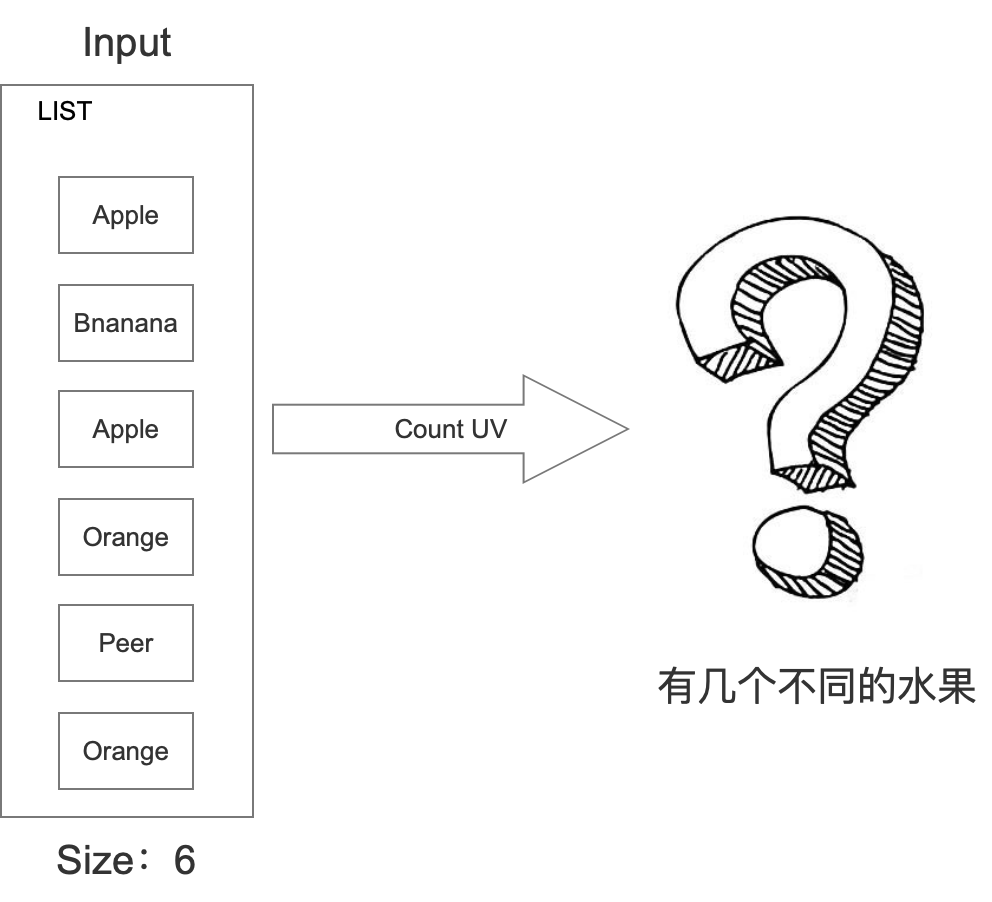
针对这个问题，我们想到的最简单的方式就是利用STL中的set处理。

SET

上架一个水果的时候，也同时在set中插入。最后需要统计的时候，直接计算set中一共有几个水果即可。具体如下所示：



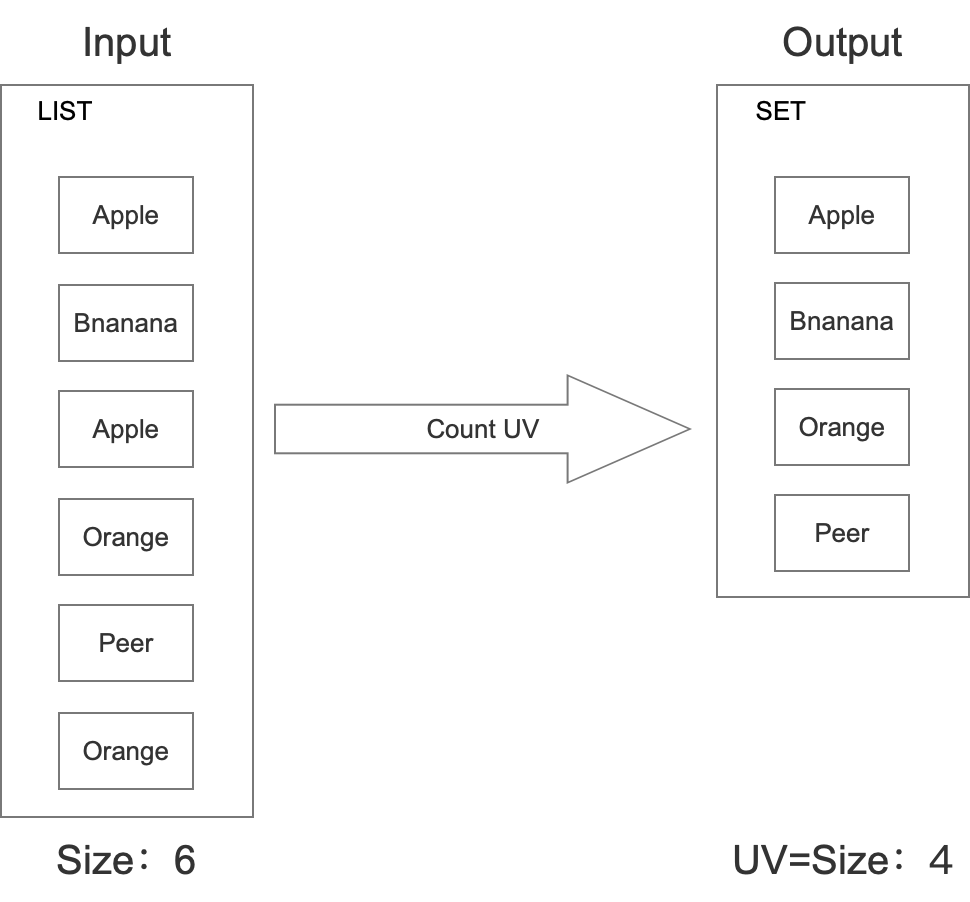
这种方式准确率是绝对准确的，但是这种方式耗费的内存是很大的。

假设每个水果需要 K 字节，那么如果有 M 个水果，一共需要 K * M 字节。那么我们能不能缩小这里的内存呢？

稍微损失一点准确率换取内存？具体见下面HashMap的方式

HASHMAP

这种算法在上架一个水果的时候，只需要在特定的位置置1即可，而不需要存储这个位置上究竟是何种水果。然后在统计的时候，只需要统计hashmap里面有多少个1即可。具体如下所示：

具体如下所示：



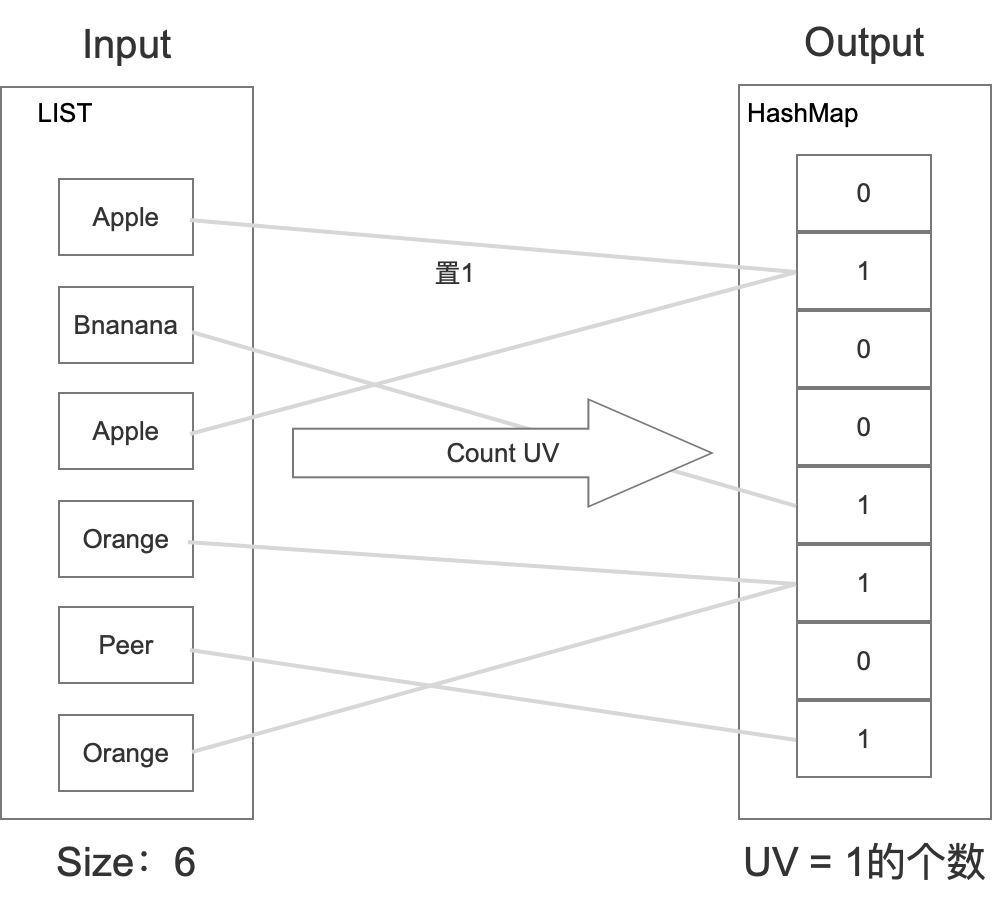
那么如果有M个水果，这里其实只需要 M / 8 字节，相比set的方式内存直接缩小到1/8。当然Hash肯定会有冲突的，所以这里肯定有一定准确率的损失。

但是如果涉及到海量数据的UV统计，这里的内存还是很大的。

能否用上统计学进一步缩小内存呢？具体见下面的Linear Count的方式。

Linear Count

这种算法在上架一个水果的时候，完全跟hashmap一致，在相应位置置1。

然后在统计的时候，利用统计学的方式，根据hashmap中零的个数给出一个估算值。具体如下所示：

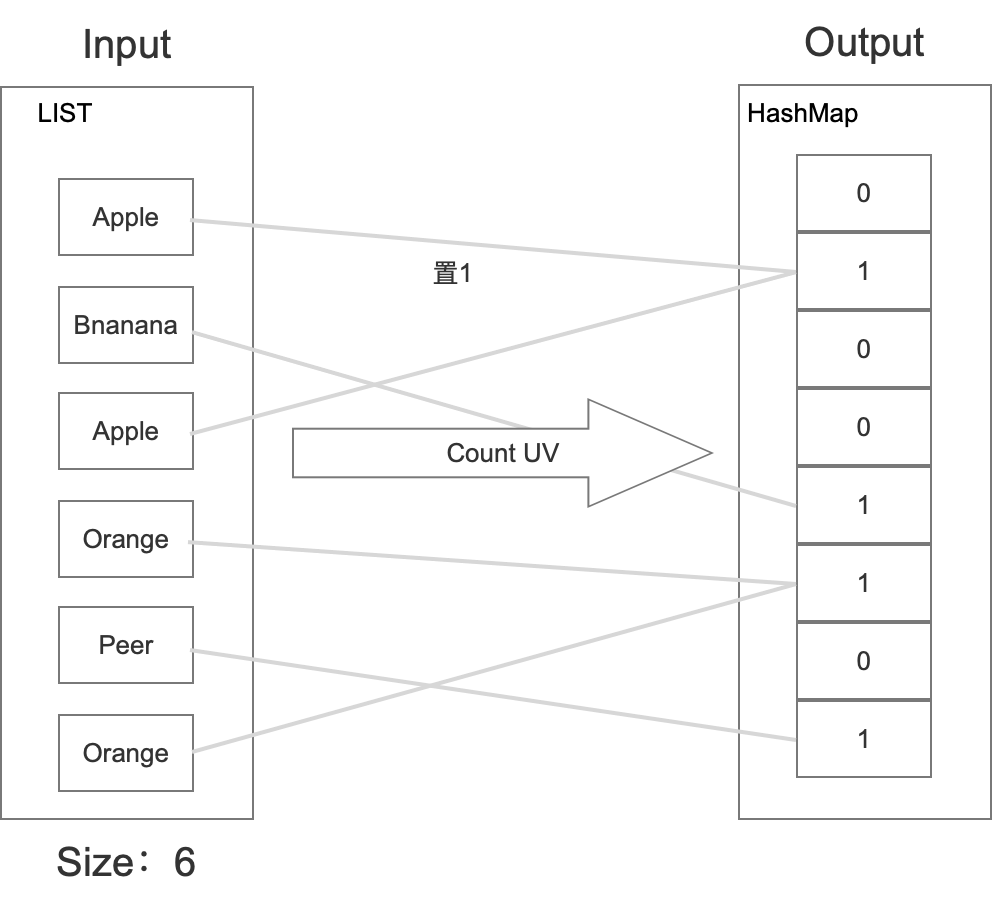
假设M为哈希桶长度，那么每次上架水果，每个桶被选中的概率为：

$$\frac{1}{M}$$

然后在上架N个元素后，某个桶为0的概率为：

$$(1-\frac{1}{M}) ^N$$

所以在上架n个元素后，哈希桶中零的个数期望为：

$$ZeroNum=\sum_{i=1}^M (1-\frac{1}{M}) ^N = M (1-\frac{1}{M}) ^N= M ((1+\frac{1}{-M})^{-M}){-\frac{N}{M}}) \approx Me^{- \frac{N}{M}}$$

所以最终：

$$

N = UV = -M ln(\frac{ZeroNum}{M})

$$

所以Linear Count算法中，只需统计下hashmap中零的个数，然后代入上式即可。

这种算法在N很小的时候，准确率是很高的，但是N很大的时候，它的准确率急剧下降。

针对海量数据的情况，LogLog Count的算法更加鲁棒

LogLog Count

这种算法跟上面几种都不同，上架水果的时候，在相应桶里面记录的是二进制数后面最长的连续零个数。然后统计的时候，利用统计学的方式，根据存储中最长连续后缀零个数，得出一个估计值。具体如下所示：

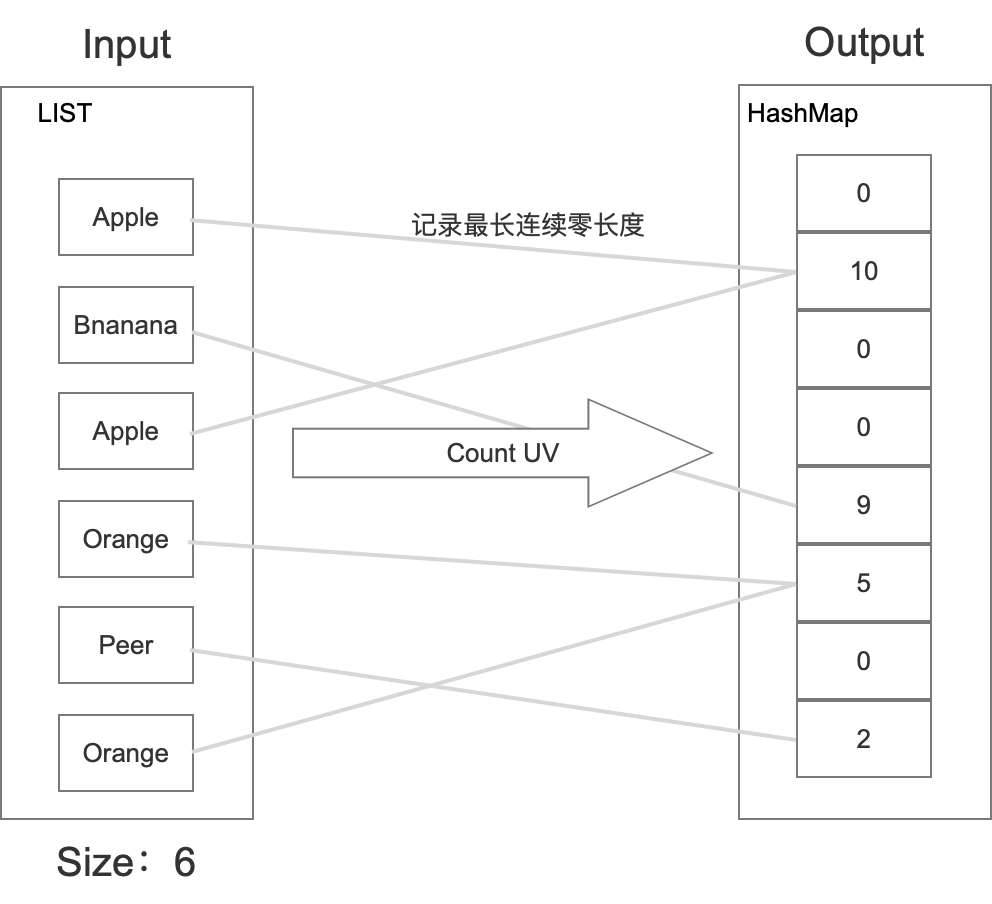
它的原理如下：

这里如果只使用一个桶来估计的话，它的误差是很大，需要用分桶平均的方式来减少它的误差。

分桶平均

既然这里利用了分桶来减少误差，那么这里统计的时候就必须合起来，这里有4种方式：

• 算术平均：$$UV=\frac{\sum_{j=1}^mUV_j} { m}$$
• 几何平均：$$UV=\sqrt[m]{UV_1...UVm}$$
• 调和平均：$$UV=\frac{m}{\sum_{j=1}^mUV_j{-1}}$$
• 中位数：$$UV=mediam {UV_1,...,UV_m}$$

LogLog Count利用的是算术平均的方式，所以最终估计值为：

$$UV=2^{{\frac{\sum_{j=1}}m{UV_j}}{m}}$$

这种算法对于基数大的情况下准确率挺高的，但是基数小的情况下准确率很低。

HyperLogLog Count

这种算法跟LogLog Count 类似，有个区别点就是它在求均值的时候利用了调和平均数，而不是算术平均数。这里最终估计值为：

$$UV=mm(\sum_{j=1}^m{2{-M_j}})^{-1}$$

然后它还引入了分段误差修正。

误差修正

具体可以看我github上的代码：HyperLogLog

总结

	准确率	内存	耗时
Set	绝对准确	K * M	O(Mlog(M))
HashMap	很高	M/8	O(M)
Linear Count	基数小高，基数大低	M/8	O(M/8)
LogLog Count	基数小低，基数大高
HyperLogLog Count	高